Различные способы нахождения периметра

Периметр многоугольника

Любой многоугольник — это замкнутая ломаная линия.

Чтобы найти длину ломаной линии, нужно сложить длины ее отрезков-звеньев.

Значит, периметр многоугольника — это сумма длин всех его сторон.

В математике периметр обозначают буквой P (пэ).

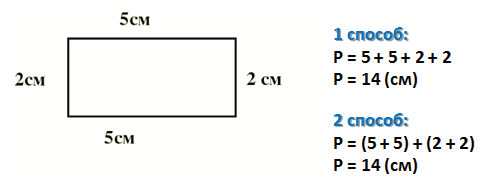
Периметр прямоугольника

Например, найдём периметр данного прямоугольника.

Этим способом мы пользуемся до тех пор, пока не выучили действие умножение.

Мы знаем, что периметр прямоугольника – сумма длин всех его сторон.

Формула для подсчета периметра прямоугольника:

(a + b) • 2

a – длина прямоугольника

b – ширина прямоугольника.

Сумма длины и ширины (a + b) называется полупериметром, чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, то есть умножить на 2.

Воспользуемся формулой периметра прямоугольника и найдем периметр прямоугольника со сторонами 2 см и 6 см:

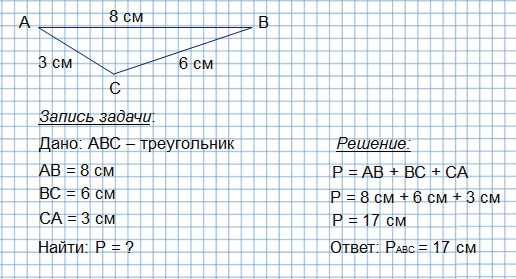
Периметр треугольника

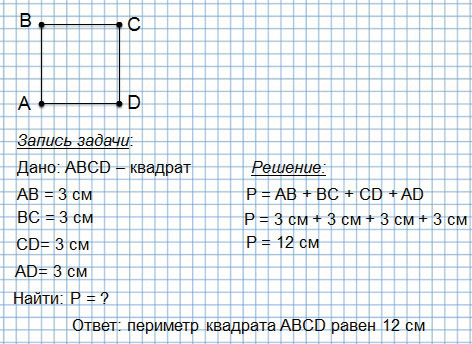
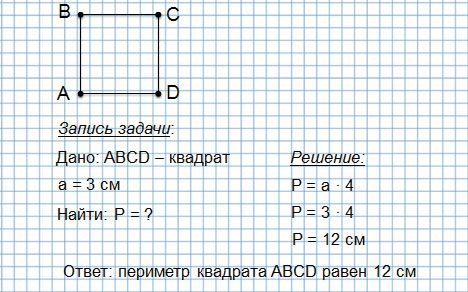
Периметр квадрата

Первый способ (когда мы еще не знаем действие умножения):

Второй способ (когда мы изучили действие умножения):

Поделись с друзьями в социальных сетях:

Источник

Периметр

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.

Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».

KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Источник

Как найти периметр прямоугольника

О чем эта статья:

Основные определения

Прямоугольником принято называть четырехугольник, у которого равны все углы. Они также являются прямыми и составляют 90°.

Периметр — это длина всех сторон многоугольника. Общепринятое обозначение — заглавная латинская буква P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.

Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Формула нахождения периметра прямоугольника

Способ вычисления нужно выбрать, отталкиваясь от исходных данных. Далее рассмотрим четыре классические формулы.

Когда известны все или две соседние стороны

P = a + b + c + d, где a, b, c, d — стороны.

Когда известна любая сторона и площадь

P = 2 * (a + S : a), где a — сторона, S — площадь.

Площадь — это плоскость внутри замкнутой геометрической фигуры.

Когда известна любая сторона и диагональ

P = 2 * (a + √(d 2 — а 2 )), где a — сторона, d — диагональ.

Диагональ — это отрезок, который соединяет противоположные стороны фигуры.

Когда известна одна любая сторона и радиус описанной окружности

P = 2 * (a + √(4 * R 2 — a 2 )), где a — сторона, R — радиус окружности.

Радиус — отрезок, соединяющий центр и любую точку окружности.

Решение задач

А теперь практиковаться!

1. Одна сторона прямоугольника 9 см, а другая на 11 см длиннее. Как узнать периметр?

• Если a = 9, то b = 9 + 11;
• Тогда b = 20 см;
• Воспользуемся формулой P = 2 * (a + b);
• P = 2 * (9 + 20);

2. Площадь прямоугольника составляет 60 м², ширина равна 15 м. Чему равен периметр фигуры?

• Для использования формулы P = 2 * (a + b), нам нужно найти длину;
• Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 60 : 15 = 4;
• Далее подставляем известные переменные в формулу: (15 + 4) * 2 = 38;

А еще можно вот так:

• Воспользуемся формулой P = 2 * (a + S : a);
• P = 2 * (15 + 60 : 15);

Ответ — такой же, 38 м.

3. Как найти периметр прямоугольника, если его диагональ в два раза больше длины равной 8 см?

• Если a = 8, то d = 8 *2;
• Тогда d = 16;
• Воспользуемся формулой P = 2 * (a + √(d 2 — а 2 ));
• P = 2 * (8 + √(16 2 — 8 2 ));

Источник

Что такое периметр геометрической фигуры

В данной публикации мы рассмотрим, что такое периметр геометрической фигуры, как он считается, а также разберем примеры для демонстрации практического применения теоретических знаний.

Определение периметра

Периметр – это сумма длин всех сторон геометрической фигуры (треугольника, квадрата, трапеции, ромба и т.д.).

Для измерения периметра используются единицы длины: миллиметры (мм), сантиметры (см), метры (м), километры (км) и т.д.

Общепринятое обозначение периметра – это латинская буква “P“, под которой можно добавить сокращенное название фигуры или ее обозначение. Например:

• Периметр треугольника можно записать как “P_треуг.“ или “P_△“;
• Периметр квадрата – “P_квадр.“ или “P_□“

Формулы периметра распространенных фигур

» data-lang=»default» data-override=»<"emptyTable":"","info":"","infoEmpty":"","infoFiltered":"","lengthMenu":"","search":"","zeroRecords":"","exportLabel":"","file":"default">» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Фигура	Название	Пояснение
«>	Квадрат	» data-order=»«>	Прямоугольник	«>
«>	Треугольник	Pквадр. = 5 + 5 + 5 + 5 = 4 ⋅ 5 = 20 см. Пример 2 Вычислим периметр прямоугольника с длиной 8 см и шириной 6 см. Pпрямоуг. = 6 + 8 + 6 + 8 = (6 + 8) ⋅ 2 = 28 см. Пример 3 Найдем периметр шестиугольника ниже. P = AB + BC + CD + DE + EH + HA = 5 + 3 + 5 + 4 + 6 + 5 = 28. Источник Как найти периметр фигуры О чем эта статья: Определение периметра Периметром принято называть длину всех сторон многоугольника. Какой буквой обозначается периметр — заглавной латинской P. Под обозначением «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения. Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения. Читайте также:  Тест финансовое планирование как способ повышения благосостояния семьи В чем измеряется периметр: Формула нахождения периметра Рассмотрим пять фигур. Треугольник Периметр треугольника — это сумма длин трех его сторон. P = a + b + c, где a, b, c — длина стороны. Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три. P = 3 * a, где a — длина стороны. Квадрат и ромб Периметр квадрата — это произведение длины стороны на четыре. Формула ромба выглядит идентично. P = 4 * a, где a — длина стороны. Прямоугольник и параллелограмм Периметр прямоугольника — сумма длины и ширины, умноженная на два. Формула параллелограмма выглядит соответственно. P = 2 * (a + b), где a — ширина, b — высота. Записывайтесь на онлайн уроки по математике к лучшим преподавателям! Уроки для учеников с 1 по 11 классы! Равнобедренная трапеция Формула для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны. P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон. Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи. L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14. Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур! Решение задач Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры? Для использования формулы P = 2 * (a + b), нам нужно найти ширину; Так как S = a * b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см; Далее подставляем известные переменные в формулу: (10 + 8) * 2 = 36 см; Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны? Используя формулу P = a + b + c вычислим сумму двух неизвестных сторон: 40 — 6 = 34 см; Известно, что равнобедренный треугольник имеет две равные стороны; Далее делим получившуюся сумму на два: 34 : 2 = 17 см; Ответ: две другие стороны равны 17см. Круг вписан в квадрат, его сторона равна 20 см. Найти периметр круга. Периметр круга равен длине ограничивающей его окружности. Значит P = L = d * π; Сторона квадрата для круга является диаметром, поэтому P = 20 * 3,14; Источник Оцените статью Вам также может понравиться Ясень семена способ распространения Ясень обыкновенный Fraxinus excelsior – так в ботанической Ярлыки способы создания ярлыков ос windows Создаем ярлыки на рабочем столе Windows Создаем ярлыки Японское удобрение фуджима способ применения Удобрения Фуджима Знаете потрясающее удобрение, палочка Японский чай способ заварки Технология заваривания японского чая Известно, что Правообладателям Политика конфиденциальности Контакты