Различают следующие способы дискретной оптимизации

Дискретная оптимизация (Дайняк А.Б.)

ПО ДИСКРЕТНОЙ ОПТИМИЗАЦИИ:

Содержание лекции: Вводная часть: задачи дискретной оптимизации — Ликбез, касающийся теории сложностей — Две больший области оптимизации: непрерывная и дискретная — Задача о кратчайшем пути — Задача о рюкзаке — Задача о потоках в сети — Задача о покрытии графов — Задачи NP hard — Курсы на курсере «Discret optimisation» P. van Hentenryck — Императивное программирование (противопоставляется программированию в ограничениях) — Курс Clare Mattieu «Approximation Algon» — без программирования — Задачи распознавания/оценивания/поиска

Содержание лекции: Классы P и NP, задача о рюкзаке — сведение задач друг к другу — неточное решение задач оптимизации — линейное программирование

Содержание лекции: Повторение прошлой лекции. Задачи вершинного покрытия. Search space. Вероятностное округление. Отличие от порогового округления. Утверждение 1 (Вероятность того, что фиксированный столбец матрицы останется непокрытым после t раундов, оценивается e в степени -t). Утверждение 2 (Связь веса покрытия и OPT). Определение матожидания.

Содержание лекции: Двойственность в ЛП — VERTEX COVER — Утверждение 1 (об оценивании целевой функции снизу) — Задача о невзвешенном вершинном покрытии — Алгоритм для weighted vertex cover — ЛП и KNAPSACK

Источник

Методы решения задач дискретной оптимизации.

Задачи дискретной оптимизации – это задачи, в которых на варьируемые значения накладываются требования дискретности.

g(x) .=)bj, xj принадлежит Dj – множеству допустимых значений параметра xj.

Классификация задач дискретной оптимизации: В зависимости от характера изменения параметров различают: полностью дискретные, частично-дискретные, целочисленные задачи и задачи с булевыми переменными.

1) Метод отсечений – предназначен для решения линейных целочисленных или частично целочисленных задач.

2) Комбинаторные методы 3) Приближенные методы

1) Метод отсечения. Решение задач целочисленной линейной оптимизации методом отсечений сводится к решению последовательности спец. образом построенных задач P0,P1,Ps. Задача P0 образуется из исходной задачи путем отбрасывания условия целочисленности. Каждая последующая задача P1,P2…Ps, образуется из предыдущей путем добавления к ней дополнительных линейных ограничений, которые называются правильным отсечением. Методы отсечения различаются между собой способами формирования дополнительных ограничений. Наиболее распространенным является метод отсечения Гомори.

Основные шаги метода ГОМОРИ.

1) Определение оптимального решения исходной задачи без учета требований целочисленности. Условие целочисленности отбрасывается и задача решается обычным симплекс- методом.

2) Если полученное решение целочисленное – то работа алгоритма заканчивается, в противном случае переход к шагу 3

3) На основании последней симплекс таблицы формируем отсечение ГОМОРИ. ∑xj >=, s номер строки таблицы , которой соответствует переменная с наибольшей дробной частью.

4) Добавление дополнительных ограничений к условию решаемой задачи: ∑xj -xd=, где xd- дополнительная переменная, умноженная на -1 — ∑xj +xd=-.Добавляется к последней симплекс таблице и полученная задача решается двойственным сиплекс методом.

5) Переход к шагу 2.

Недостатки; метод может использоваться для решения частично- целочисленных задач. Недостатки: метод используется для решения линейно-целочисленных задач. В процессе решения при добавлении дополнительных ограничения размер задачи возрастает.

2) Комбинаторные методы. К ним относятся метод ветвей и границ, он используется как для решения линейных так и нелинейных задач. Основан на использовании конечности множества допустимых вариантов и замене полного перебора частичным перебором. Полного перебора удается избежать путем отбрасывания неперспективных множеств, т.е. множеств, где заранее нет перспективного решения. В процессе поиска строится дерево вариантов. Каждой подвершине дерева вариантов соответствует подзадача исходной задачи.

3) Приближённые методы. Для точного алг-ма нужно знать трудоёмкость и память. Для приближенного алгоритма, кроме трудоемкости и памяти, вводят такие параметры, как относительная погрешность еА алгоритма А и вероятность несрабатывания 6А алгоритма А.

Постановка задач нелинейного программирования. Задачи выпуклого программирования. Функция Лагранжа, принципы ее построения. Метод множителей Лагранжа для решения задач на условный экстремум.

1) В общем виде задача нелинейной оптимизации может быть сформулирована в следующем виде: f(x)->max (min);

gi(x) bi, i=1..m. При этом хотя бы одна из функций f(x) или gi(x) является нелинейной. Задача с ограничениями называется задачей с условной оптимизацией , а задачи без ограничений- задачи безусловной оптимизации.

Для задач безусловной оптимизации необходимое условие экстремума заключается в том, что в оптимальной точке все частные производные целевой функции должны быть равны 0. Для проверки достаточного условия экстремума необходимо построить матрицу вторых производных G(x*)целевой функции в оптимальной точке.

Характер точки X* связан со знакоопределенностью квадратичной формы : X T G(X*)X, x не равен 0.

Данная квадратичная форма является положительно определенной если она > 0, отрицательно определенной если она =0, отрицательнополуопреленная

Если квадратичная форма в точке х* является положительноопределенной, то в этой точке функция имеет локальный минимум, если квадратичная форма является отрицательноопределенной, то в этой точке функция имеет локальный максимум. Если она является неопределенной, то функция не имеет экстремума в данной точке, если функция является полуопределенной, то требуетсядополнительное исследование.

Для проверки знакоопределенности используют критерий Сильвестра, согласно которому квадратичная форма положительноопределена тогда, когда все главные миноры матрицы G(x*) положительны, квадратичная форма отрицательно определена, когда первый угловой минор отрицательный, а далее знаки чередуются +,-.

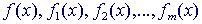
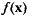
2) Задачи выпуклого программирования. Задачей выпуклого программирования называется задача нелинейного программирования, у которой все функции являются выпуклыми функциями. Общая задача выпуклого программирования состоит в отыскании такого вектора х (т. е. такой точки выпуклого допустимого множества), который является минимум выпуклой функции или максимум вогнутой функции

3) Функция Лагранжа, принцип ее построения.

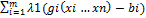
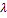
F(x1,x2…xn, λ1…λm)=f(x1…xn)+ , — являются произвольными числами и называются множителями Лагранжа.

4) Метод множителей Лагранжа позволяет находить экстремум функции при ограничениях – равенствах.

— Составляется функция Лагранжа.

— Определяются частные производные функции Лагранжа по всем переменным и приравниваются к 0. В итоге получается система из n+m уравнений с n+m неизвестными, решая эту систему уравнений получаем точки подозрительные на экстремум.

Найденные точки дальше исследуются на минимум или максимум.

Дальнейшее исследование проводится как в случае безусловной оптимизации, т.е строится матрица вторых производных и сравниваются значения главных миноров.

Источник

Различают следующие способы дискретной оптимизации

Отыщи всему начало, и ты многое поймёшь

Какое умение самое важное?
– Умение спрашивать.

Что такое оптимизация вообще? Наиболее просто – это выбор наилучшего варианта из множества возможных по некоторому критерию. Если критерий выбора известен и вариантов немного, то решение может быть найдено путём простого перебора и сравнения всех вариантов.

Однако часто бывает так, что число возможных вариантов настолько велико, что полный перебор практически невозможен. В таких случаях приходится формулировать задачу на языке математики и применять специальные методы поиска оптимального решения, т.е. методы оптимизации.

Одной из основных задач оптимизации является так называемая задача математического программирования, которая в общем случае состоит в нахождении такого вектора х = (х₁, х₂, …, х_n), при котором достигается наибольшее или наименьшее значение непрерывной функции f(x), при условии, что x ∈ M, где M – допустимая область, представляющая собой некоторое подмножество всего пространства.

Математическая форма записи этой задачи (для определённости сформулируем её как задачу максимизации, хотя она ничем не отличается от задачи минимизации) такова:

Функцию f(x) называют целевой, а условия, описывающие множество М, – системой ограничений. В зависимости от вида этой функции и свойств допустимой области M задача математического программирования относится к тому или иному классу.

Существуют различные принципы классификации задач математического программирования. Одной из важнейших задач математического программирования является задача линейного программирования – в ней целевая функция и система ограничений являются линейными функциями.

В теории и практике математического программирования важную роль играют задачи целочисленного (дискретного) программирования, когда все переменные в задаче должны принимать только целочисленные (не дробные) значения. Это связано с физической неделимостью многих объектов расчёта.

Все методы дискретной оптимизации и соответствующие им алгоритмы по основной идее каждого из них можно разделить на три большие группы:

• отсечения;
• комбинаторные (переборные);
• приближённые.

Джордж Бернард Данциг
(1914—2005)

Остановимся подробнее на этих методах.

1. Методы отсечения. Исторически исследованиям задач дискретной оптимизации предшествовало развитие теории и методов линейного программирования, в частности, создание Джорджем Данцигом симплекс-метода как универсального метода решения задач линейного программирования.

Естественны были попытки представить исходную дискретную задачу как задачу целочисленного линейного программирования и свести её решение к использованию уже имевшихся методов решения непрерывных линейных задач, в частности, симплекс-метода.

Однако простое округление получаемых значений переменных не приводило к успеху. Поэтому была разработана следующая, более сложная процедура решения целочисленной задачи линейного программирования, известная под названием методов отсечения.

Методы отсечения сводят решение задачи целочисленного линейного программирования к решению последовательности специальным образом построенных задач линейного программирования. Впервые эта идея для задач целочисленного линейного программирования была высказана тем же Дж. Данцигом.

Она состоит в следующем. Если полученное решение удовлетворяет условию целочисленности, то процесс окончен. В противном случае к ограничениям исходной задачи добавляется новое линейное ограничение, обладающее двумя свойствами:

• полученное нецелочисленное решение ему не удовлетворяет;
• любое целочисленное решение ему удовлетворяет.

Далее снова решается задача линейного программирования с дополнительно введенным ограничением (отсечением), процесс повторяется до получения целочисленного решения.

Другими словами, отсекается ненужное решение непрерывной задачи и исключается возможность потери решения целочисленной задачи. Снова решается задача без условия целочисленности. Процесс продолжается до тех пор, пока оптимальное решение не окажется целочисленным.

Реализация метода отсечения предполагает решение следующих трёх проблем:

• нахождение универсального правила формирования отсечений;
• доказательство конечности процесса отсечения;
• борьба с чрезмерным ростом размерности задач при добавлении ограничений.

Эти проблемы впервые были решены с помощью алгоритмов Р. Гомори, который сформулировал универсальное правило формирования отсечений и доказал конечность процесса отсечений.

Однако в дальнейшем выявилась большая непредсказуемость в поведении различных алгоритмов отсечения. Оказалось, что количество шагов существенно зависит не только от размерности задачи, но и от конкретных числовых данных. Были обнаружены задачи относительно небольшой размерности, решение которых требует больших затрат машинного времени.

В дальнейшем методы отсечения не нашли широкого применения при решении прикладных задач целочисленного линейного программирования по следующим причинам:

• сложно определить, какое отсечение (из большого их числа) является наилучшим;
• методы отсечения приспособлены в основном для решения чисто целочисленных задач, которые составляют лишь малую часть задач, встречающихся в приложениях;
• методы отсечения не приспособлены для решения разреженных задач целочисленного линейного программирования.

2. Комбинаторные (переборные) методы. Здесь необходимо вначале определить понятие оптимизационно-комбинаторной задачи. Это можно сделать следующим образом.

Пусть имеется множество из n элементов. На этом множестве задаётся множество комбинаций P = <p₁, p₂, …, p_n>, где под комбинациями понимаются сочетания, подстановки, перестановки, свойственные каждой конкретной задаче. На множестве Р задаётся некоторая функция f. В оптимизационно-комбинаторной задаче ищется экстремум функции f (максимум или минимум) и отыскиваются те элементы множества P, на которых функция f экстремальна.

Приведём в качестве примера популярную задачу о ранце (или рюкзаке), которая получила название от конечной цели: уложить как можно большее число ценных вещей в рюкзак при условии, что вместимость рюкзака ограничена. С различными вариациями задачи о рюкзаке можно столкнуться в экономике, прикладной математике, криптографии и логистике.

В общем виде задачу можно сформулировать так: из заданного множества предметов со свойствами «стоимость» и «вес» требуется отобрать подмножество с максимальной полной стоимостью, соблюдая при этом ограничение на суммарный вес.

При решении оптимизационно-комбинаторных задач необходимо следующее:

• нужно уметь перебирать множество значений функции f;
• вычислять эти значения и сравнивать.

Для решения оптимизационно-комбинаторных задач было разработано большое число методов, основная идея которых состоит в использовании конечности множества допустимых решений и замене полного их перебора сокращённым (направленным или неявным перебором).

Главную роль в сокращении перебора играют оценка и отбрасывание неперспективных подмножеств, заведомо не содержащих оптимальных решений. Отбрасывание таких подмножеств позволяет заменить полный перебор частичным и, тем самым, уменьшить затраты вычислительных ресурсов.

Комбинаторные методы различаются способом разбиения и способом оценивания, эти способы обычно связаны со спецификой решаемых классов задач. Правила, в соответствии с которыми производится отсев подмножеств, заведомо не содержащих оптимальных решений, называются правилами отсева.

В настоящее время наиболее широко применяемыми являются три группы методов:

• локальная оптимизация;
• случайный поиск;
• методы ветвления.

Рассмотрим кратко суть этих методов.

При локальной оптимизации для каждой комбинации p_i ∈ P определяется множество Q_i – множество комбинаций, соседних с p_i. Исходной операцией является случайный выбор начальной комбинации. Затем на множестве Q_i находят локальный экстремум. Этот процесс повторяется многократно, и среди полученных локальных экстремумов выбирается наименьший и именно он принимается за приближённое значение.

При случайном поиске выбор всех комбинаций происходит случайно согласно некоторому закону распределения. Значения целевой функции на этих комбинациях вычисляются, и среди них выбирается та комбинация, которая даёт экстремальное значение целевой функции.

Основной проблемой при случайном поиске является выбор существенных признаков комбинаций. Здесь наиболее популярны два подхода:

• признаки выбираются заранее путём анализа условий задачи;
• признаки получают из анализа уже полученных решений.

3. Методы ветвления. Впервые метод ветвей и границ был предложен для решения задач целочисленного линейного программирования.

В дальнейшем этот метод был применён к более общим классам комбинаторных оптимизационных задач. По способу ветвления все алгоритмы ветвей и границ можно разделить на следующие группы:

1. Алгоритмы, строящие дерево подзадач исходной задачи (например, алгоритм Лэнд и Дойга, предложенный для решения задач целочисленного программирования. В этом методе строится дерево задач линейного программирования, добиваясь постепенного удовлетворения условий целочисленности – вариант метода отсечений);
2. Алгоритмы, строящие дерево недопустимых решений (например, аддитивный алгоритм Балаша и его модификации). Этот метод применяется для решения задач линейного программирования с булевыми переменными;
3. Алгоритмы, строящие дерево допустимых решений (например, метод решения задач о коммивояжере).

Для примера ввиду большой популярности и распространённости задачи о коммивояжере, опишем последовательность действий (алгоритм) в методе ветвей и границ для этой задачи:

• выбирается некоторая полная ветвь и вычисляется длина маршрута; эту ветвь называют эталонной;
• рассматриваются другие начальные участки маршрута; для каждого из них последовательно вычисляются оптимистические оценки нижней границы длины маршрута;
• сравнивается оценка очередного участка маршрута с длиной эталонной ветки:
• если оптимистическая оценка больше длины эталонной ветви, то участок – бесперспективный, и дальше ветвление делать не нужно,
• иначе, из конечной вершины участка осуществляется ветвление, то есть перебор участков, содержащих на одну вершину больше, чем рассматриваемый участок.

Процесс продолжается до получения полной последовательности.

Если длина маршрута, соответствующая эталонной последовательности, меньше длины эталонной ветви, то её принимают за эталонную.

Последняя эталонная последовательность будет оптимальной.

В настоящее время сформулировано большое количество оптимизационных комбинаторных задач, имеющих широкие практические приложения. Ввиду их популярности, перечислим лишь названия (по названию примерно можно судить о содержании задачи) некоторых из них, не вдаваясь в их содержание:

• задача о ранце;
• задача о коммивояжере;
• задача минимизации среднего времени обработки партии деталей;
• задача о назначениях;
• задача о покрытии;
• задача компоновки;

Разработано также целый ряд комбинаторных методов. Снова перечислим только названия тех методов, которые наиболее часто применяются при решении приведенных задач:

• метод последовательного анализа вариантов;
• метод ветвей и границ;
• локальные алгоритмы;
• методы, основанные на последовательностных схемах;
• метод динамического программирования;
• аппроксимационно-комбинаторный метод.

Отметим, что все приведенные методы являются универсальными, и именно их универсальность обусловливает чрезвычайную широту их применения к конкретным задачам.

На основе этих методов иногда разрабатываются гибридные методы.

4. Приближённые методы. Эти методы широко применяются при решении задач с приближённым решением, так как нахождение точного решения может потребовать значительных вычислительных ресурсов.

Современные приближённые методы обычно являются комбинированными, т.е. содержат в себе элементы различных методов. В приближённых методах решение задачи производится обычно в два этапа: построение начального решения и улучшение начального решения.

При этом на первом этапе широко используются эвристические алгоритмы ‑ алгоритмы, основанные на правдоподобных, но не обоснованных строго предположениях о свойствах оптимального решения задачи.

Примером эвристического алгоритма может быть алгоритм решения задачи коммивояжера, в котором на каждом шаге реализуется переход в ближайшую из оставшихся точек. Алгоритмы такого типа носят название «greedy» («жадные» или пожирающие алгоритмы).

Эти алгоритмы на каждом шаге решают «локальную» задачу оптимизации; однако полученное решение может быть сколь угодно далёким от оптимума. На втором этапе используются алгоритмы локальной оптимизации, связанные с введённым понятием окрестности; при этом можно использовать несколько алгоритмов этого типа, изменяя правила выбора окрестности.

В основном, приближённые методы базируются на отказе от поиска точного решения и введении взамен этого дополнительного условия прекращения процесса оптимизации.

Например, вместо поиска x ∈ M, для которого f(x) минимальна, ставится задача поиска такого x* ∈ M, что f(x₀) – f(x*) 0. То есть фактически условия подобного рода требуют поиска лишь точек, в которых функция существенно убывает, но минимума может и не достигать.

Основанием для перехода к приближённым методам являются такие признаки задачи:

• экспоненциальный (очень быстрый) рост объёма вычислений с ростом размерности задач; это явление получило название «проклятие размерности»;
• для точного решения задач большой размерности нужны мощные компьютеры, а приближённые решения можно получить на имеющихся;
• в прикладных задачах, как уже отмечалось, часто исходную задачу удаётся сформулировать лишь приближённо, тогда точное решение не имеет смысла и может представлять скорее теоретический интерес;
• исходные данные в прикладной задаче известны, как правило, приближённо, соответственно приближёнными являются и параметры модели, и поиск точного решения не оправдан.

От приближённых методов, гарантирующих поиск решения с заданной точностью, следует отличать различного рода «эвристические» методы, которые таких свойств получаемых решений не гарантируют.

Их использование оправдано только при полном отсутствии других возможностей. Отметим также, что существуют задачи, в которых требуются точные решения, например, требуется дать ответ «да» или «нет».

А.А. Антонюк , кандидат физико-математических наук

Источник