ДЕТАЛЬНАЯ РАЗБИВКА КРУГОВЫХ КРИВЫХ
Детальная разбивка кривой предусматривает не только закреп-ление на местности начала НК, конца КК и середины СК кривой, но и обозначение всей кривой, например, колышками через определен-ный интервал. Существует ряд способов разбивки круговых кривых: способ прямоугольных координат, способ углов, способ продолжен-ных хорд.
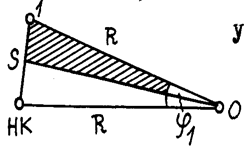
Способ прямоугольных координат (ординат от тангенса).
|


|
|
|
|
|
|
В эти формулы подставляют значение угла j1, зависящее от величины интервала К, которое можно найти из выражения:
j1= 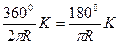
На местности откладывают от начала кривой НК по направ-лению на вершину угла поворота ВУ (по направлению тангенса) абсциссы Хi , а по перпендикулярному направлению ординаты Уi и закрепляют точки 1, 2, 3 и т.д. Так производят разбивку до середины кривой. Другую половину кривой разбивают с ее конца. Для определения координат Х и У существуют специальные таблицы.
Этот способ применяется на ровной площадке и является наиболее точным, так как точки 1, 2, 3 и т.д. выносят независимо друг от друга, поэтому ошибка положения одной точки не окажет влияния на положение других точек, чего нельзя сказать о рассмат-риваемых далее способах углов и продолженных хорд .
Способ углов (полярный способ).
|
|
|
|
|
Этот способ удобно применять в стесненных условиях, когда есть видимость между НК и точками 1, 2, 3. (например, на высокой насыпи, где способ прямоугольных координат неприемлем).
|
|

|
|
|
|
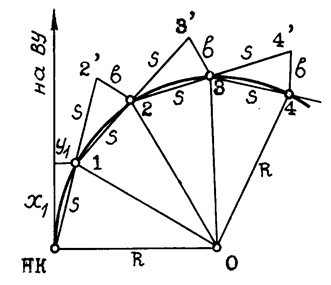
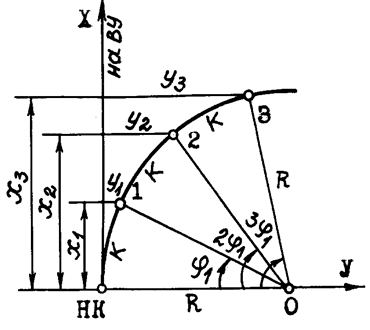
Способ продолженных хорд
|
Вначале по координатам Х1 и У1 выносят точку 1. Затем в створе НК-1 на расстоянии S от точки 1 отмечают вспомогательную точку 2’, от которой откладывают так называемое промежуточное
|
|
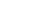




|
|
Этим способом одну половину кривой разбивают с HK, а дру-гую половину — с конца кривой КК. Способ применим в любыхстес-ненных условиях, в том числе и в выемке, где первые два способа неприемлемы.
Недостатком способов углов и продолженных хорд является снижение точности разбивки кривой по мере возрастания ее длины, так как положение каждой последующей точки определяется относительно предыдущей.
Источник
Детальная разбивка круговых кривых
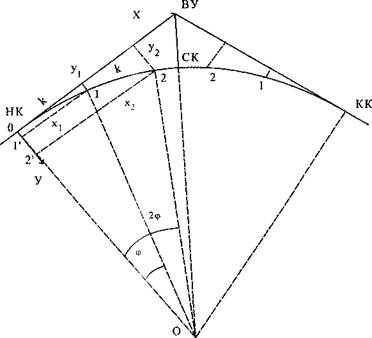
Детальная разбивка переходных и круговых кривых выполняется в период строительства после выноса на трассу трех основных точек кривой НК, СК, КК. Детальная разбивка производится через 5 м при радиусах кривых менее 100 м, через 10 м при радиусах кривых менее 500 м и через 20 м – более 500 м. Для детальной разбивки кривых наиболее часто используется способ прямоугольных координат (рис. 3).
Рис. 3 Способ прямоугольных координат
За начало координат принимают точку НК – начала круговой кривой, ось X располагают по тангенсу кривой в направлении ВУ, ось У направлена по радиусу к центру круговой кривой О.
Выбирают интервал разбивки К и для этого значения рассчитывают угол φ = (К/R)ρ, по которому определяют значения прямоугольных координат х и у для детальной разбивки.
Вдоль тангенсов (ось абсцисс) откладывают длины х, восстанавливают прямой угол в полученной точке. Точка 1 круговой кривой фиксируется расстоянием у, отмеренным по перпендикуляру. Так же и получают другие точки круговой кривой. Вторую половину круговой кривой разбивают от ее конца, выполняя аналогичные действия и используя значения х и у, полученные для первой половины. Как видно из геометрии способа, для его реализации требуется свободное пространство. Достоинство способа прямоугольных координат состоит в том, что каждая точка кривой выносится независимо от других с примерно одинаковой точностью.
Если участок трассы расположен в закрытой местности, то удобнее использовать способ продолженных хорд (рис. 4).
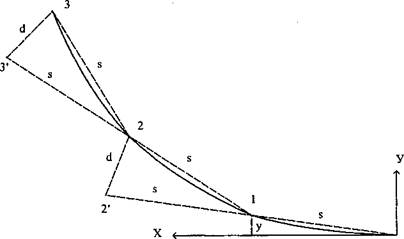
Рис. 4 Способ продолженных хорд
В этом способе первая точка выносится по способу прямоугольных координат. Затем хорда продолжается на ее же длину s, и получается вспомогательная точка 2′. На базе 12′ при помощи линейной засечки расстояниями s и d =s2/R получается точка 2 круговой кривой. Вновь продолжают хорду, но уже от точки 2. вдоль отрезка 21. Из точек 23′ повторяют линейную засечку отрезками s и d, получая точку 3 и т.д.
В некоторых случаях при трассировании объектов возникает необходимость выноса пикета на круговую кривую.
Вынос осуществляется методом прямоугольных координат (рис. 5)
Вначале вычисляется значение К – интервала круговой кривой между пикетом и началом круговой кривой.
Зная К можно получить угол φ
Используя значение φ получим координаты x и y
Источник
Детальная разбивка кривых различными методами
Детальная разбивка кривых различными методами
В лабораторной работе рассмотрен метод прямоугольных координат.
8.1 Исходные данные. Целью настоящей работы является определение координат главных и промежуточных точек круговой кривой, составление плана и перенесении их в натуру.
Данные для решения задачи:
8.1.1 Угол поворота трассы θ°:
Радиус круговой кривой R
8.1.2 Координаты точки начала кривой (НК) и дирекционный угол трассы αАС:
8.1.3 Прямоугольные координаты Х и У определить для каждого 5-ти метрового участка кривой.
8.2 Методические указания:
8.2.1 Необходимо вычислить следующие элементы круговой кривой по формулам:
Тангенс – длина касательной
Биссектриса Б = СО – R = Rsec
Длина кривой
8.2.2 Следует определить координаты точек середины и конца кривой, вершины угла поворота, а также точки О. Составить план разбивки круговой кривой в масштабе 1: 1000.
8.3 Выполнить детальную разбивку горизонтальной кривой, для этого:
8.3.1 Вычислить величину угла Өо, соответствующего заданной дуге Кгор:
Өо = 180 х Кгор/ 
где 
8.3.2 Приняв начало координат в точке НК, касательную НК – ВУ за ось абсцисс, а линию НК – О за ось ординат, вычисляют координаты точек кривой до ее середины (СК) по формулам:
Х1 = RsinӨо; Y1 = R(1 – cosӨо);
Х2 = Rsin2Өо; Y2= R(1 – cos2Өо);
Х3 = Rsin3Өо. Y3= R(1 – cos3Өо).
8.3.3 Для контроля правильности вычислений аналогичные расчеты координат точек кривой производят от конца кривой (КК), приняв его за начало координат.
8.3.4 Результаты расчетов должны быть представлены в виде таблицы.
8.3.5 На план разбивки круговой кривой в масштабе 1: 1000 нанести точки круговой кривой по соответствующим координатам.
8.3.6 На местности выполнить вынос в натуру основных элементов круговой кривой и ее детальную разбивку
8.3.6 Самостоятельно выполнить детальную разбивку круговой кривой способом продолженных хорд и углов и хорд.
Способ продолженных хорд (рисунок 8.2). Точку В на кривой определяют линейной засечкой из точек А и В’, откладывая из точки А лентой хорду d и рулеткой из точки В’ отрезок у. Точку В’ определяют путем откладывания по оси абсцисс хорды d. По направлению АВ (продолжение хорды) откладывают хорду d и получают точку С’. Отложив от точки В хорду d и от С’ отрезок к линейной засечкой получают точку С и т. д. Из подобных треугольников ОВС и ВС’С получают:
Так как в треугольнике АВ’В угол В’АВ равен ц/2, то можно считать у = к/2.
Рисунок 8.2 – Способ продолженных хорд
Способ углов и хорд основывается на том, что углы с вершиной в какой-либо точке круговой кривой, образованные касательной и секущей и заключающие равные дуги, равны половине соответствующего центрального угла (рисунок 8.3).
Для разбивки кривой при помощи углов и хорд вычисляют центральный угол 

Рассчитывают углы 
Сначала выполняют разбивку кривой от её начала НКК до середины СКК. Затем, освободив алидаду, в сторону кривой откладывают от тангенса угол 

Источник

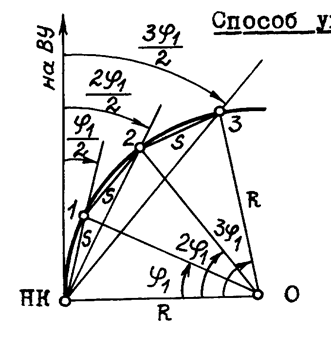
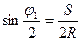 (из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.
(из решения заштрихованного треугольника), причем в этом способе S явля-ется хордой определенной длины.