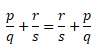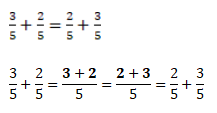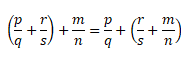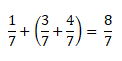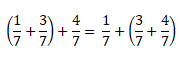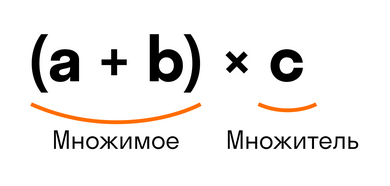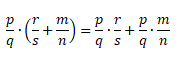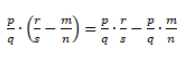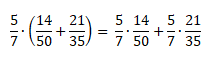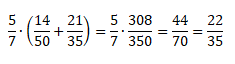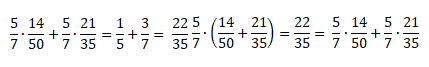Рациональный способ вычисления переместительный

Свойства умножения

Переместительное свойство умножения

От перестановки сомножителей местами произведение не меняется.

Следовательно, для любых чисел a и b верно равенство:

выражающее переместительное свойство умножения.

4 · 2 · 3 = 3 · 2 · 4 = 24.

Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.

Сочетательное свойство умножения

Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.

Следовательно, для любых чисел a, b и c верно равенство:

выражающее сочетательное свойство умножения.

3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30

3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.

Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:

25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.

В данном случае можно было вычислить всё последовательно:

25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,

но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.

Распределительное свойство умножения

Сначала рассмотрим распределительное свойство умножения относительно сложения:

Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Следовательно, для любых чисел a, b и m верно равенство:

выражающее распределительное свойство умножения.

Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.

Следовательно, для любых чисел a, b и m верно равенство:

Теперь рассмотрим распределительное свойство умножения относительно вычитания:

Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

Переход от умножения:

соответственно к сложению и вычитанию:

называется раскрытием скобок.

Переход от сложения и вычитания:

называется вынесением общего множителя за скобки.

Источник

Рациональные приёмы вычислений на уроках математики

Разделы: Математика

Класс: 4

Ключевые слова: математика

«Мозг хорошо устроенный ценится больше,
чем мозг хорошо наполненный.»

Умения рационально производить вычисления характеризуют довольно высокий уровень математического развития. Знакомство и применение рациональных способов вычислений развивает вариативность мышления, показывает ценность знаний, которые при этом используются. Эти умения чрезвычайно сложны, формируются они медленно и за время обучения в начальной школе далеко не у всех детей могут быть достаточно сформированы.

Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро. Считать в уме можно только при большом желании и систематической тренировки. И тогда перед вами откроется совсем другая математика: живая, полезная, понятная.

Скажите, пожалуйста, как рациональнее сложить 1+ 7, 4 * 8? Какие законы применили?

27 + 46+13? 27 – 19 – 7? Какие свойства, законы? Т.е основы рациональных приёмов вычислений основаны на чём?

Методика преподавания математики в начальных классах раскрывает основы рациональных приёмов вычислений, связанных с выполнением разных математических действий с натуральными числами.

Рациональные приёмы сложения основываются

1. Коммуникативный закон сложения а +в =в +а

2. Ассоциативный закон сложения а+в+с = а+ (в+с)

на коммуникативном и ассоциативном приёмах сложения, а так же свойствах изменения суммы. Рассмотрим некоторые из них.

Свойства сложения.

1.1

а+в+с =У, то (а – к) +с+в = У –к

38+24+15 = 77, то 36+ 24+ 15 = ?

а+в+с=У, то (а+ к) +в +с = У+к

38 + 24+15 = 77, то 40+ 24 + 15 =?

1.2.

а+ в =С , то (а +к ) + (в – к) = С

56 + 27 = 83, то (56 + 4) + (27 – 4) = ?

Какие ещё рациональные приёмы сложения можно применить на уроке математики?

Округление одного из слагаемых; поразрядного сложения; приём группировки вокруг одного и того же «корневого» числа.

Рассмотрим эти приёмы:

13 + 49 + 76 + 61 = (поразрядное сложение)

38 + 59 = 38 + (…округление слагаемого)

26 + 24 + 23 +25 + 24 = (группировка вокруг одного и того же «корневого» числа

Все приёмы рациональных вычислений, связанных с вычитанием, основываются на законах вычитания.

Если уменьшаемое увеличить или уменьшить на число, то соответственно разность увеличится или уменьшится на это же самое число

а – в = С, то (а +к) — в = С +к

74 – 28 = 46, то 77 – 28 = 49

а-в = С , то (а – к ) — в = С-к

74 – 28 = 46, то 71 – 28 = 43

Если вычитаемое увеличить или уменьшить на несколько единиц, то разность измениться в противоположную сторону.

Если уменьшаемое и вычитаемое уменьшить или увеличить на одно и тоже число, то разность не измениться.

Найди верные равенства.

229 – 36 = (229 – 9 ) – ( 36 – 6)

174 – 58 = (174 – 4) – ( 58 – 4)

358 – 39 = ( 358 – 8 ) – (39 – 8)

617 – 48 = ( 617 – 7 ) – (48 – 8)

Для рациональных вычислений используют частичные приёмы умножения и деления.

Приём замены множителя или делителя на произведение.

75 * 8 = 75 * 2*2*2=

960 : 15 = 960 : 3 : 5 =

Приём умножения на 9, 99,999, 11 …

87 * 99 = 87 * 100- 87 = 8700 – 87 = 8613

87 * 11 = 87 *10 + 87 = 870+ 87 = 957

Успешное применение различных приёмов зависит от умения подмечать особенности чисел и их сочетаний. Например, познакомив детей в первом классе с натуральным рядом чисел и имея его перед глазами, легко закрепить состав числа.

0 1 2 3 4 5 6 7

Отработав, таким образом, состав чисел в пределах 10 и познакомившись с переместительным законом сложения, дети легко справляются с заданием найти сумму чисел в пределах 10, а в дальнейшем, используя переместительное и сочетательное свойство сложения, легко можно найти сумму других чисел. Например:

48 +14 +22 +36 =120

Существуют приёмы на знаниях некоторых свойств чисел или результатов действий. Легко находить сумму последовательных нечётных чисел, начиная с 1.

Она равна произведению количества слагаемых на самого себя. (проверить)

Рационализация может осуществляться за счет возможности выполнять некоторые арифметические действия. Для этого очень важно научить детей внимательно рассматривать условия задания, суметь подметить все его особенности. Такие задания, как поставь нужный знак действия16 … 17 = 33 ( рассуждать), далее подобные задания усложняются. 8…6…33 = 15

Сравни, не вычисляя

51 : 3 … 30 : 3 + 21 :5

636 :6 … 600 : 6+ 30 : 6+ 6 :6

Задания могут даваться в занимательной форме: Математический лабиринт, составь слово, найди пару , расшифруй пословицу и т.д.

Используй рациональные приёмы вычисления, разгадай слово

Какие приёмы использовали?

Важно показать ученикам красоту и изящество устных вычислений, используя разнообразные вычислительные приёмы, помогающие значительно облегчить процесс вычисления.

СЧЁТ НА ПАЛЬЦАХ: способ быстрого умножения чисел первого десятка на 9. Допустим нам надо умножить 7 на 9. Повернём ладошки к себе, загнём седьмой палец, число пальцев слева от загнутого пальца – это число десятков, а число – справа, количество единиц.

Все задания, которые рассматривались, воспитывают интерес к математике, развивают их математические способности. Такую работу можно продолжать на математическом кружке.

Источник

Законы математики

О чем эта статья:

Переместительный закон сложения

Начнем изучать основные законы математики со сложения натуральных чисел.

Переместительный закон сложения

От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:

m + n = n + m

Переместительный закон сложения работает для любых чисел.

Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.

Приведем пример с весами, которые используют продавцы в магазинах.

Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.

При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.

Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:

Формула переместительного закона для обыкновенных дробей:

Чтобы сложить две дроби нужно сложить числители, а знаменатель оставить прежним. Вот так:

Сочетательный закон сложения

Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.

Сочетательный закон сложения: два способа

1. Результат сложения нескольких слагаемых не зависит от порядка действий.
2. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел.

Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.

Рассмотрим сумму из трех слагаемых:

Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:

• 1 + 3 + 4 = (1 + 3) + 4 = 5 + 4 = 8

Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:

• 1 + 3 + 4 = 1 + (3 + 4) = 1 + 7 = 8

В обоих случаях получается один и тот же результат — что и требовалось доказать.

Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:

Отразим сочетательный закон сложения с помощью переменных:

(a + b) + c = a + (b + c)

Формула сочетательного закона для обыкновенных дробей:

Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.

Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.

Значит, сочетательный закон справедлив и для обыкновенных дробей.

Переместительный закон умножения

С каждым новым правилом решать задачки по математике все интереснее.

Переместительный закон умножения

От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.

Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:

В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.

Переместительный закон умножения с помощью переменных выглядит так:

a * b = b * a

Сочетательный закон умножения

Рассмотрим еще один полезный закон в математике.

Сочетательный закон умножения

Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.

Другими словами, умножайте числа в любом порядке — как вам больше нравится.

Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:

А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:

• 3 * 4 = 12
• 2 * 12 = 24
• 2 * 3 * 4 = 24

Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.

• (2 * 3) * 4 = 2 * (3 * 4)
• 6 * 4 = 2 * 12
• 24 = 24

Для любых натуральных чисел a, b и c верно равенство:

a * b * с = (a * b) * с = a * (b * с)

Пример

Вычислить: 5 * 6 * 7 * 8.

Это выражение можно вычислять в любом порядке. Вычислим слева направо:

5 * 6 * 7 * 8 = 1680

Распределительный закон умножения

Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:

Распределительный закон умножения

• Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
• Чтобы сумму чисел умножить на число, нужно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:

Сначала выполним действие в скобках:

В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:

Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:

• (3 + 5) * 2 = 3 * 2 + 5 * 2
• 3 * 2 = 6
• 5 * 2 = 10
• 6 + 10 = 16

Отразим распределительный закон умножения с помощью переменных:

(a + b) * c = a * c + b * c

Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.

Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.

Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:

c * (a + b) = c * a + c * b

Пример 1

Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:

5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25

Пример 2

Найти значение выражения 2 * (5 + 2).

Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:

2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14

Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.

Пример 3

Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:

4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16

Распределительный закон умножения для суммы обыкновенных дробей:

Распределительный закон умножения для разности обыкновенных дробей:

Проверим справедливость этого закона:

Посчитаем, чему равна левая часть равенства.

Теперь посчитаем, чему равна правая часть равенства.

Так мы доказали справедливость распределительного закона.

Задания для самопроверки

Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂

Задание 1. Найти значение выражения: 8 * (1 + 6).

Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).

Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).

Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).

Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)

Задание 6. Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?

Задание 7. В смартфоне 32 гб памяти. Какое количество приложений можно установить, если одно занимает 1,2 гб?

Задание 8. Верно ли равенство: 8 * 5 = 49?

Источник