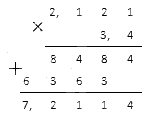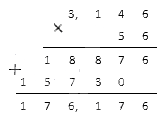Рациональный способ вычисления 5 класс примеры

Урок математики 5 класс Бунимович Е.А. по теме «Рациональные вычисления»
план-конспект урока по математике (5 класс) по теме

Урок математики 5 класс Бунимович Е.А.

Скачать:

Вложение	Размер
02_racion_vich.pptx	147.12 КБ
munitsipalnoe_byudzhetnoe_obshcheobrazovatelnoe_uchrezhdenie_buturlinskaya.docx	197.06 КБ
skrin_virtualnoy_laboratorii.docx	97.82 КБ

Предварительный просмотр:

Подписи к слайдам:

Метапредмет – Изменение и развитие РАЦИОНАЛЬНЫЕ ВЫЧИСЛЕНИЯ. ИСПОЛЬЗОВАНИЕ СВОЙСТВ ДЕЙСТВИЙ ПРИ ВЫЧИСЛЕНИЯХ

Ключевые слова урока целеполагание Определи ключевые слова и сформулируй цель урока РАЦИОНАЛЬНО ВЫЧИСЛЯТЬ АЛЬНОРАЦИОН ЧИС ВЫ ЛЯТЬ проверить

Математический тренинг Организация и самоорганизация учащихся. Организация обратной связи 1) Каждое числовое равенство иллюстрирует некоторое свойство сложения или умножения. Запишите каждое из свойств в буквенном виде и назовите его. Числовое равенство Буквенное равенство 4 + 5 = 5 + 4 3 ∙ 7 = 7 ∙ 3 (5 + 4) + 1 = 5 + (4 + 1) (3 ∙ 6) ∙ 5 = 3 ∙ (6 ∙ 5)

Математический тренинг Организация и самоорганизация учащихся. Организация обратной связи 2.Может ли: а) сумма двух чисел равняться одному из слагаемых? б) произведение двух чисел равняться одному из множителей? Запишите соответствующие свойства сложения и умножения в буквенном виде. 3.Найдите значение выражения: а) 2 ∙ 3 2 ; б) 4 2 + 14; в) 2 2 ∙ 7 ∙ 25; г) 5 2 + 25; д) 4 ∙ 9 ∙ 5 2 ; е) 100 – 2 ∙ 5 2 ; ж) 99 +43 з )75 ∙ 7 ∙ 16 ∙ 15

Организация и самоорганизация учащихся. Организация обратной связи ! Пример 3). 75 ∙ 7 ∙ 16 ∙ 15. 75 ∙ 7 ∙ 16 ∙ 15 = (25 ∙ 3) ∙ 7 ∙ (4 ∙ 4) ∙ 15 = (25 ∙ 4) ∙ (3 ∙ 7) ∙ (4 ∙ 15) = = 100 ∙ 21 ∙ 60 = (21 ∙ 6) ∙ 1000 = 126000 УДОБНЫЕ МНОЖИТЕЛИ Нам удалось легко вычислить произведение, выделив удобные множители: 2 и 5, 4 и 25, 50 и 2, 20 и 5, 125 и 8 и т.д. Пример ж). 99 + 43 = 99 + (1 + 42 )=( 99 + 1 ) + 42 = 100 + 42 = 142

№ 222(а) № 222(б) 36 ∙ 25 = (9 ∙ 4) ∙ 25= (25 ∙ 4) ∙ 9 = 100 ∙ 9 = 900 25 ∙ 12 = 25 ∙ (3 ∙ 4) = (25 ∙ 4) ∙ 3 = 100 ∙ 3 = 300

Осваиваем алгоритмы Проверка полученных результатов. Коррекция. Запишите цепочку преобразований и вычислите результат: ТРЕНАЖЕР № 96 а) 85 + 27 + 15 = ответ (85 + 15) + 27 = 127 б) 49 + 63 + 11 + 17 = ответ (49 + 11) + (63 +17) = 140 Вычислите произведение: УЧЕБНИК № 223

Вычисление произведений Практикум Вычислите произведение: УЧЕБНИК № 223 В качестве образца используйте пример 3. (стр. 67) б) 16 ∙ 125 ∙ 4 ∙ 35 = ответ ( 8 ∙ 2 ) ∙ 125 ∙ 4 ∙ 5 ∙ 7 = 280000 Критерии оценки За каждое задание ставится: 2 балла – записано рациональное вычисление и получен верный ответ 1 балл – записан только верный ответ 0 баллов – решено не верно Максимальное количество 6 баллов — «5» 4-5 баллов — «4» 2-3 балла — «3»

Подведение итогов, рефлексия, домашнее задание. Вариантов решения поставленных задач может быть несколько. Но если они верны, то любой приведет к правильному результату. Вопрос только времени. Домашнее задание З: № 17 3 ( б , г) – записать цепочки, № 174, 175(б). *Э.У:№223(а)(электронное приложение к учебнику) *Творческое задание: придумать жизненную задачу , в решении которой нужно применить рациональный способ вычисления. Разная алгебра

Источник

Рациональные приёмы вычислений на уроках математики

Разделы: Математика

Класс: 4

Ключевые слова: математика

«Мозг хорошо устроенный ценится больше,
чем мозг хорошо наполненный.»

Умения рационально производить вычисления характеризуют довольно высокий уровень математического развития. Знакомство и применение рациональных способов вычислений развивает вариативность мышления, показывает ценность знаний, которые при этом используются. Эти умения чрезвычайно сложны, формируются они медленно и за время обучения в начальной школе далеко не у всех детей могут быть достаточно сформированы.

Говорят, если хотите научиться плавать, вы должны войти в воду, а если хотите уметь решать задачи, то должны начать их решать. Но для начала надо освоить азы арифметики. Научиться считать быстро. Считать в уме можно только при большом желании и систематической тренировки. И тогда перед вами откроется совсем другая математика: живая, полезная, понятная.

Скажите, пожалуйста, как рациональнее сложить 1+ 7, 4 * 8? Какие законы применили?

27 + 46+13? 27 – 19 – 7? Какие свойства, законы? Т.е основы рациональных приёмов вычислений основаны на чём?

Методика преподавания математики в начальных классах раскрывает основы рациональных приёмов вычислений, связанных с выполнением разных математических действий с натуральными числами.

Рациональные приёмы сложения основываются

1. Коммуникативный закон сложения а +в =в +а

2. Ассоциативный закон сложения а+в+с = а+ (в+с)

на коммуникативном и ассоциативном приёмах сложения, а так же свойствах изменения суммы. Рассмотрим некоторые из них.

Свойства сложения.

1.1

а+в+с =У, то (а – к) +с+в = У –к

38+24+15 = 77, то 36+ 24+ 15 = ?

а+в+с=У, то (а+ к) +в +с = У+к

38 + 24+15 = 77, то 40+ 24 + 15 =?

1.2.

а+ в =С , то (а +к ) + (в – к) = С

56 + 27 = 83, то (56 + 4) + (27 – 4) = ?

Какие ещё рациональные приёмы сложения можно применить на уроке математики?

Округление одного из слагаемых; поразрядного сложения; приём группировки вокруг одного и того же «корневого» числа.

Рассмотрим эти приёмы:

13 + 49 + 76 + 61 = (поразрядное сложение)

38 + 59 = 38 + (…округление слагаемого)

26 + 24 + 23 +25 + 24 = (группировка вокруг одного и того же «корневого» числа

Все приёмы рациональных вычислений, связанных с вычитанием, основываются на законах вычитания.

Если уменьшаемое увеличить или уменьшить на число, то соответственно разность увеличится или уменьшится на это же самое число

а – в = С, то (а +к) — в = С +к

74 – 28 = 46, то 77 – 28 = 49

а-в = С , то (а – к ) — в = С-к

74 – 28 = 46, то 71 – 28 = 43

Если вычитаемое увеличить или уменьшить на несколько единиц, то разность измениться в противоположную сторону.

Если уменьшаемое и вычитаемое уменьшить или увеличить на одно и тоже число, то разность не измениться.

Найди верные равенства.

229 – 36 = (229 – 9 ) – ( 36 – 6)

174 – 58 = (174 – 4) – ( 58 – 4)

358 – 39 = ( 358 – 8 ) – (39 – 8)

617 – 48 = ( 617 – 7 ) – (48 – 8)

Для рациональных вычислений используют частичные приёмы умножения и деления.

Приём замены множителя или делителя на произведение.

75 * 8 = 75 * 2*2*2=

960 : 15 = 960 : 3 : 5 =

Приём умножения на 9, 99,999, 11 …

87 * 99 = 87 * 100- 87 = 8700 – 87 = 8613

87 * 11 = 87 *10 + 87 = 870+ 87 = 957

Успешное применение различных приёмов зависит от умения подмечать особенности чисел и их сочетаний. Например, познакомив детей в первом классе с натуральным рядом чисел и имея его перед глазами, легко закрепить состав числа.

0 1 2 3 4 5 6 7

Отработав, таким образом, состав чисел в пределах 10 и познакомившись с переместительным законом сложения, дети легко справляются с заданием найти сумму чисел в пределах 10, а в дальнейшем, используя переместительное и сочетательное свойство сложения, легко можно найти сумму других чисел. Например:

48 +14 +22 +36 =120

Существуют приёмы на знаниях некоторых свойств чисел или результатов действий. Легко находить сумму последовательных нечётных чисел, начиная с 1.

Она равна произведению количества слагаемых на самого себя. (проверить)

Рационализация может осуществляться за счет возможности выполнять некоторые арифметические действия. Для этого очень важно научить детей внимательно рассматривать условия задания, суметь подметить все его особенности. Такие задания, как поставь нужный знак действия16 … 17 = 33 ( рассуждать), далее подобные задания усложняются. 8…6…33 = 15

Сравни, не вычисляя

51 : 3 … 30 : 3 + 21 :5

636 :6 … 600 : 6+ 30 : 6+ 6 :6

Задания могут даваться в занимательной форме: Математический лабиринт, составь слово, найди пару , расшифруй пословицу и т.д.

Используй рациональные приёмы вычисления, разгадай слово

Какие приёмы использовали?

Важно показать ученикам красоту и изящество устных вычислений, используя разнообразные вычислительные приёмы, помогающие значительно облегчить процесс вычисления.

СЧЁТ НА ПАЛЬЦАХ: способ быстрого умножения чисел первого десятка на 9. Допустим нам надо умножить 7 на 9. Повернём ладошки к себе, загнём седьмой палец, число пальцев слева от загнутого пальца – это число десятков, а число – справа, количество единиц.

Все задания, которые рассматривались, воспитывают интерес к математике, развивают их математические способности. Такую работу можно продолжать на математическом кружке.

Источник

Приёмы рациональных вычислений.

Одно из самых важных умений человека – это умение быстро и правильно выполнять вычисления.

Рационализация вычислений означает выполнение вычислений более лёгким, более целесообразным способом.

Устные вычисления способствуют активизации мыслительной деятельности, развитию логического мышления, сообразительности, памяти, творческих начал и волевых

качеств. Способность к умственному (устному) счёту полезна

в отношении практическом и, как средство, для здоровой умственной гимнастики.

1. Приём, основанный на использовании свойств

арифметических действий.

· 89 + 67 + 11 = 89 + 11 + 67 = 167

· 357 + 996 + 48 = 357 + 996 + (43 + 4 + 1) =

= (357 + 43) + (996 + 4) + 1 = 400 + 1000 +1 = 1401

· 25 × 37 × 4 = 37 × (25 × 4) = 37 × 100 =3700

· 87 × 4 + 4 × 13 = (87 + 13) × 4 = 100 × 4 = 400

· 367 : 5 – 167 : 5 = ( 367 – 167) : 5 = 200 : 5 = 40

2. Приём округления.

· 399 + 473 = 400 +472 = 872

· 497 + 196 + 299 = 492 + 200 + 300 = 992

· 196 + 199 + 197 = 200 × 3 – 8 = 592

· 752 – 298 = 754 – 300 = 454

· 134 + 27 + 29 + 38 = 150 + 20 + 30 + 37 = 200 + 37 = 237

· 427 + 28 + 7 + 20 + 652 = 430 + 649 + 30 + 5 + 20 =

= 1079 + 1 + 54 = 1080 + 20 + 34 = 1134

· 198 × 3 = (200 – 2) × 3 = 600 – 6 = 594

· 35 × 18 = 35 × (20 – 2) = 700 – 70 = 630

3. Приём, основанный на зависимости результата от

изменения компонентов действий.

· 56 – 38 = 60 – 42 = 18

· 225 : 75 = (225 2) : (75 2) = 450 : 150 = 3

· 440 : 55 = 880 : 110 = 8

· 364 : 6 + 118 : 3 = 364 : 6 + 236 : 6 = (364 + 236) : 6 = 600 : 6 = 100

4. Приёмы последовательного умножения и деления.

· 75 × 8 = 75 × 2 × 2 × 2 = 150 × 2 × 2 = 300 × 2 = 600

· 35 × 18 = 35 × 2 × 9 = 70 × 9 = 630

· 23 × 55 = 23 × (5 × 11) = 115 × 11 = 1150 + 115 = 1 265

· 540 : 4 = (540 : 2) : 2 = 270 : 2 = 135

· 960 : 15 = (960 : 3) : 5 = 320 : 5 = 64

5. Приёмы умножения и деления на 5, 50, 500, 25, 250, 15, 125.

· 36 × 5 = (36 : 2) × 10 = 180

· 826 × 50 = (826 : 2) × 100 = 41 300

· 84 × 25 = (84 : 4) × 100 = 2 100

· 24 × 15 = 12 × 30 = 360

· 496 × 125 = (496 : 8) × 1000 = 62 000

· 4 340 : 5 = (4 340 : 10) × 2 = 868

· 4 000 : 125 = (4 000 × 8) : (125 × 8) = 32 000 : 1 000 = 32

6. Приёмы умножения на 9, 99, 11, 101. 1001.

· 26 × 9 = 25 × (10 – 1) = 250 – 25 = 225

· 35 × 99 = 3 500 – 35 = 3 465

· 37 × 11 = 37 × (10 + 1) = 370 + 37 = 407

· 73 × 101 = 7 300 + 73 = 7 373

· 735 × 1 001 = 735 000 + 735 = 735 735

Так, наблюдая и выявляя свойства чисел и действий над

ними, ученики накапливают сведения и используют их затем при

вычислениях. Овладение некоторыми приёмами рациональных

вычислений готовит детей к успешному изучению математики в

Источник

Действия с рациональными числами: правила, примеры, решения

Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.

Действие сложения рациональных чисел

Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5 + 1 4 возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.

Сформулируем правила сложения рациональных чисел:

Сложение нуля с отличным от него рациональным числом

Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства: a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a .

Пара простых примеров: сумма рационального числа 2 , 1 и числа 0 равно 2 , 1 и: 6 4 5 + 0 = 6 4 5 .

Сложение противоположных рациональных чисел

Сумма противоположных чисел равна нулю.

Данное правило можно записать в виде: a + ( — a ) = 0 (для любого рационального числа a ).

К примеру, числа 45 , 13 и — 45 , 13 являются противоположными, т.е. их сумма равно нулю: 45 , 13 + ( — 45 , 13 ) = 0 .

Сложение положительных рациональных чисел

В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.

Необходимо произвести сложение рациональных чисел: 0 , 6 и 5 9 .

Решение

Выполним перевод десятичной дроби в обыкновенную и тогда: 0 , 6 + 5 9 = 6 10 + 5 9 .

Осуществим сложение дробей с разными знаменателями:

6 10 + 5 9 = 54 90 + 50 90 = 104 90 = 1 7 45

Ответ: 0 , 6 + 5 9 = 1 7 45 .

Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.

Сложение рациональных чисел с разными знаками

Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.

Необходимо осуществить сложение рациональных чисел с разными знаками 8 , 2 и — 2 3 4 .

Решение

Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: | 8 , 2 | = 8 , 2 и | — 2 3 4 | = 2 3 4 . Проведя сравнение модулей — рациональных чисел, получим: 8 , 2 > 2 3 4 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое — вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8 , 2 — 2 3 4 = 8 2 10 — 2 3 4 = 5 9 20 .

Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8 , 2 + ( — 2 3 4 ) = 5 9 20 .

Сложение отрицательных рациональных чисел

Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.

Необходимо произвести сложение чисел: — 4 , 0203 и — 12 , 193 .

Решение

Модули заданных чисел соответственно равны: 4 , 0203 и 12 , 193 . Сложим их:

​​​​​​

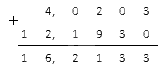
Полученному результату присваиваем знак минус: — 16 , 2133 .

Ответ: ( — 4 , 0203 ) + ( — 12 , 193 ) = — 16 , 2133 .

Действие вычитания рациональных чисел

Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c + b = a следует, что a — b = c и a — c = b . И наоборот: из равенств a — b = c и a — c = b следует, что c + b = a .

При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.

Необходимо вычислить разность рациональных чисел: 4 , ( 36 ) – 1 5 .

Решение

Сначала переведем периодическую десятичную дробь в обыкновенную: 4 , ( 36 ) = 4 + ( 0 , 36 + 0 , 0036 + … ) = 4 + 0 , 36 1 — 0 , 01 = 4 + 36 99 = 4 + 4 11 = 4 4 11

Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4 , ( 36 ) — 1 5 = 4 4 11 — 1 5 = 4 + 4 11 — 1 5 = 4 + 20 55 — 11 55 = 4 + 9 55 = 4 9 55

Ответ: 4 , ( 36 ) — 1 5 = 4 9 55

В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + ( — b ) .

Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: ( a + ( — b ) ) + b = a + ( ( — b ) + b ) = a + 0 = a . Отсюда в силу смысла действия вычитания следует, что сумма a + ( — b ) есть разность чисел a и b .

Необходимо из рационального числа 2 7 вычесть рациональное число 5 3 7

Решение

Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. — 5 3 7 . Тогда: 2 7 — 5 3 7 = 2 7 + — 5 3 7

Далее произведем сложение рациональных чисел с разными знаками: 2 7 + — 5 3 7 = — 5 3 7 — 2 7 = — 5 3 7 — 2 7 = — 5 1 7

Ответ: 2 7 + — 5 3 7 = — 5 1 7

Действие умножения рациональных чисел

Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.

Умножение на нуль

Произведение любого рационального числа a на нуль есть нуль.

Используя переместительное свойство умножения, получим: 0 · а = 0 .

К примеру, умножение рационального числа 7 13 на 0 даст 0 . Перемножив отрицательное рациональное число — 7 1 8 и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0 · 0 = 0 .

Умножение на единицу

Умножение любого рационального числа a на 1 дает число a .

Т.е. a · 1 = a или 1 · a = a (для любого рационального a ). Единица здесь является нейтральным числом по умножению.

К примеру, умножение рационального числа 5 , 46 на 1 даст в итоге число 5 , 46 .

Умножение взаимообратных чисел

Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а · а — 1 = 1 .

К примеру, результатом произведения чисел 5 6 и 6 5 будет единица.

Умножение положительных рациональных чисел

В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.

Необходимо вычислить произведение положительных рациональных чисел 0 , 5 и 6 25 .

Решение

Представим заданную десятичную дробь в виде обыкновенной 0 , 5 = 5 10 = 1 2 .

Далее произведем умножение обыкновенных дробей: 1 2 · 6 25 = 6 50 = 3 25 .

Ответ: 0 , 5 · 6 25 = 3 25

Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.

Необходимо вычислить произведение рациональных чисел 2 , 121 и 3 , 4 .

Решение

Перемножим десятичные дроби столбиком:

Ответ: 2 , 121 · 3 , 4 = 7 , 2114

В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.

Умножение рациональных чисел с разными знаками

Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.

Необходимо найти произведение чисел: — 3 3 8 и 2 1 2

Решение

Согласно вышеуказанному правилу получим: — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2 = — 3 3 8 · 2 1 2

Заменим смешанные дроби неправильными и найдем искомое произведение: — 3 3 8 · 2 1 2 = — 27 8 · 5 2 = — 135 16 = — 8 7 16

Ответ: — 3 3 8 · 2 1 2 = — 8 7 16

Умножение отрицательных рациональных чисел

Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.

Необходимо найти произведение отрицательных рациональных чисел — 3 , 146 и — 56 .

Решение: модули заданных чисел соответственно равны 3 , 146 и 56 .

Перемножим их столбиком:

Полученный результат и будет являться искомым произведением.

Ответ: ( — 3 , 146 ) · ( — 56 ) = 176 , 176

Деление рациональных чисел

Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенства b · c = a следует, что a : b = c и a : c = b . И наоборот: из равенств a : b = c и a : c = b следует, что b · c = a .

На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.

Разделить число а на число b , отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a : b = a · b — 1 .

Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств ( a · b — 1 ) · b = a · ( b — 1 · b ) = a · 1 = a , которая и доказывает равенство a : b = a · b — 1 .

Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.

Необходимо выполнить действие деления 3 1 3 : — 1 1 6

Решение

Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: — 1 1 6 = — 7 6 .

Число, обратное этой дроби, будет: — 6 7 . Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 3 1 3 — 1 1 6 = 3 1 3 · — 6 7 = 10 3 · ( — 6 7 ) = — ( 10 3 · 6 7 ) = — 20 7 = — 2 6 7

Ответ: 3 1 3 : — 1 1 6 = — 2 6 7

Источник