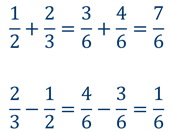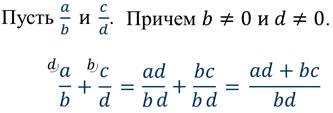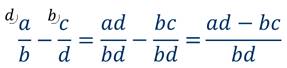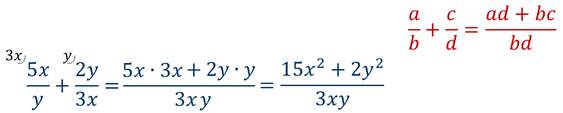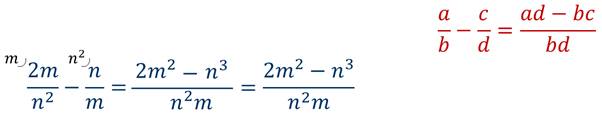Рациональный способ сложения дробей с разными знаменателями

Сложение дробей: теория и практика

О чем эта статья:

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
2. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.

Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1\4.

Основные свойства дробей

1. Дробь не имеет значения, при условии, если делитель равен нулю.

2. Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

3. Равными называются такие a/b и c/d, если:

4. Если числитель и знаменатель умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Как плюсовать дроби

Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.

Свойства сложения

• От перестановки мест слагаемых сумма не меняется: a + b = b + a.
• Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).
• Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
• При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.

Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.

Сложение дробей с одинаковыми знаменателями

Чтобы получить результат суммы двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.

Не забудьте проверить, можно ли сократить дробь.

Сложение дробей с разными знаменателями

Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:

1. Найдем наименьшее общее кратное (далее — НОК) для определения единого делителя.

Для этого записываем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

НОК (15, 18) = 3 * 2 * 3 * 5 = 90

2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

Полученные числа записываем справа сверху над числителем.

3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.

4. Проверим полученный результат:

• если делимое больше делителя, нужно преобразовать в смешанное число;
• если есть что сократить, нужно выполнить сокращение.

Еще раз ход решения одной строкой:

Сложение смешанных чисел

Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

1. Сложить целые части.

2. Сложить дробные части.

Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.

3. Суммируем полученные результаты.

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Если урок в самом разгаре и посчитать нужно быстро — можно воспользоваться онлайн-калькулятором. Вот несколько подходящих:

Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, нужно решать примеры сложения дробей, как можно чаще.

Источник

Сложение и вычитание дробей с разными знаменателями

Урок 4. Алгебра 8 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Сложение и вычитание дробей с разными знаменателями»

Сложение и вычитание рациональных дробей с разными знаменателями выполняется аналогично сложению и вычитанию дробей с одинаковыми знаменателями, но предварительно нужно дроби привести к общему знаменателю.

Аналогичным образом выполняют вычитание рациональных дробей с разными знаменателями.

Пример 1. Найти сумму дробей.

Пример 2. Найти разность дробей.

Мы рассмотрели простейшие случаи на сложение и вычитание рациональных дробей с разными знаменателями. Но чаще всего приходится сначала дроби приводить к общему знаменателю, а затем уже выполнять сложение и вычитание рациональных дробей с одинаковыми знаменателями.

Алгоритм приведения рациональных дробей к общему знаменателю:

1. Разложить знаменатели каждой из дробей на множители.

3. Для каждой из дробей найти дополнительный множитель.

4. Числитель дроби умножить на её дополнительный множитель.

5. Записать каждую дробь с числителем и общим знаменателем.

Пример 3. Найти сумму дробей.

Пример 4: Найдите разность дробей.

Алгоритм сложения (вычитания) рациональных дробей с разными знаменателями.

Для того чтобы сложить (вычесть) дроби с разными знаменателями, надо:

2. Привести дроби к общему знаменателю.

3. Сложить (вычесть) дроби по правилу сложения (вычитания) рациональных дробей с одинаковыми знаменателями.

4. По возможности упростить полученную дробь.

Задание: нужно преобразовать выражение и представьте его в виде дроби.

Для того чтобы привести рациональные дроби к общему знаменателю, надо:

1. Разложить знаменатели каждой из дробей на множители.

3. Для каждой из дробей найти дополнительный множитель.

4. Числитель дроби умножить на её дополнительный множитель.

5. Записать каждую дробь с числителем и общим знаменателем.

Для того чтобы сложить (вычесть) дроби с разными знаменателями, надо:

2. Привести дроби к общему знаменателю.

3. Сложить (вычесть) дроби по правилу сложения (вычитания) рациональных дробей с одинаковыми знаменателями.

4. По возможности упростить полученную дробь.

Источник

Сложение дробей

При сложении дробей могут встретиться разные случаи.

Сложение дробей с одинаковыми знаменателями

Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.

C помощью букв это правило сложения можно записать так:

Записывая ответ, проверьте нельзя ли полученную дробь сократить.

Сложение дробей с разными знаменателями

Чтобы сложить дроби с разными знаменателями нужно воспользоваться следующими правилами.

1. Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти наименьшее общее кратное знаменателей.

Пример. Сложить дроби.

Как найти общий знаменатель

Находим НОК (15, 18) .

НОК (15, 18) = 3 · 2 · 3 · 5 = 90

Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1) делим по очереди на знаменатель каждой дроби.

Полученные числа и будут дополнительными множителями для каждой из дробей. Множители записываем над числителем дроби справа сверху.

90 : 15 = 6 — дополнительный множитель для дроби

3

15

.

90 : 18 = 5 — дополнительный множитель для дроби

4

18

.

Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь основным свойством дроби.

После умножения в знаменателях обеих дробей должен получиться наименьший общий знаменатель. Затем складываем дроби как дроби с одинаковыми знаменателями.
Проверяем полученную дробь.

Eсли в результате получилась неправильная дробь, результат записываем в виде смешанного числа. Проверим нашу дробь.

Источник

Сложение и вычитание алгебраических дробей: правила, примеры

Данная статья начинает изучение действий с алгебраическими дробями: рассмотрим подробно такие действия как сложение и вычитание алгебраических дробей. Разберем схему сложения и вычитания алгебраических дробей как с одинаковыми знаменателями, так и с разными. Изучим, как сложить алгебраическую дробь с многочленом и как произвести их вычитание. На конкретных примерах поясним каждый шаг поиска решения задач.

Действия сложения и вычитания при одинаковых знаменателях

Схема сложения обыкновенных дробей применима и для алгебраических. Мы знаем, что при сложении или вычитании обыкновенных дробей с одинаковыми знаменателями необходимо сложить или вычесть их числители, а знаменатель остается исходным.

К примеру: 3 7 + 2 7 = 3 + 2 7 = 5 7 и 5 11 — 4 11 = 5 — 4 11 = 1 11 .

Соответственно аналогичным образом записывается правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями:

Чтобы осуществить сложение или вычитание алгебраических дробей с одинаковыми знаменателями, нужно соответственно сложить или вычесть числители исходных дробей, а знаменатель записать без изменений.

Данное правило дает возможность сделать вывод, что результат сложения или вычитания алгебраических дробей — новая алгебраическая дробь (в частном случае: многочлен, одночлен или число).

Укажем пример применения сформулированного правила.

Заданы алгебраические дроби: x 2 + 2 · x · y — 5 x 2 · y — 2 и 3 — x · y x 2 · y — 2 . Необходимо осуществить их сложение.

Решение

Исходные дроби содержат одинаковые знаменатели. Согласно правилу, выполним сложение числителей заданных дробей, а знаменатель оставим неизменным.

Сложив многочлены, являющиеся числителями исходных дробей, получим: x 2 + 2 · x · y − 5 + 3 − x · y = x 2 + ( 2 · x · y − x · y ) − 5 + 3 = x 2 + x · y − 2 .

Тогда искомая сумма будет записана как: x 2 + x · y — 2 x 2 · y — 2 .

В практике, как во многих случаях, решение приводится цепочкой равенств, наглядно показывающей все этапы решения:

x 2 + 2 · x · y — 5 x 2 · y — 2 + 3 — x · y x 2 · y — 2 = x 2 + 2 · x · y — 5 + 3 — x · y x 2 · y — 2 = x 2 + x · y — 2 x 2 · y — 2

Ответ: x 2 + 2 · x · y — 5 x 2 · y — 2 + 3 — x · y x 2 · y — 2 = x 2 + x · y — 2 x 2 · y — 2 .

Результатом сложения или вычитания может стать сократимая дробь, в этом случае оптимально ее сократить.

Необходимо вычесть из алгебраической дроби x x 2 — 4 · y 2 дробь 2 · y x 2 — 4 · y 2 .

Решение

Знаменатели исходных дробей равны. Произведем действия с числителями, а именно: вычтем из числителя первой дроби числитель второй, после чего запишем результат, оставляя знаменатель неизменным:

x x 2 — 4 · y 2 — 2 · y x 2 — 4 · y 2 = x — 2 · y x 2 — 4 · y 2

Мы видим, что полученная дробь – сократимая. Осуществим ее сокращение, преобразовав знаменатель при помощи формулы разности квадратов:

x — 2 · y x 2 — 4 · y 2 = x — 2 · y ( x — 2 · y ) · ( x + 2 · y ) = 1 x + 2 · y

Ответ: x x 2 — 4 · y 2 — 2 · y x 2 — 4 · y 2 = 1 x + 2 · y .

По такому же принципу складываются или вычитаются три и более алгебраических дробей при одинаковых знаменателях. К примеру:

1 x 5 + 2 · x 3 — 1 + 3 · x — x 4 x 5 + 2 · x 3 — 1 — x 2 x 5 + 2 · x 3 — 1 — 2 · x 3 x 5 + 2 · x 3 — 1 = 1 + 3 · x — x 4 — x 2 — 2 · x 3 x 5 + 2 · x 3 — 1

Действия сложения и вычитания при разных знаменателях

Вновь обратимся к схеме действий с обыкновенными дробями: чтобы выполнить сложение или вычитание обыкновенных дробей с разными знаменателями, необходимо привести их к общему знаменателю, а затем сложить полученные дроби с одинаковыми знаменателями.

К примеру, 2 5 + 1 3 = 6 15 + 5 15 = 11 15 или 1 2 — 3 7 = 7 14 — 6 14 = 1 14 .

Так же по аналогии сформулируем правило сложения и вычитания алгебраических дробей с разными знаменателями:

Чтобы осуществить сложение или вычитание алгебраических дробей с разными знаменателями, необходимо:

• исходные дроби привести к общему знаменателю;
• выполнить сложение или вычитание полученных дробей с одинаковыми знаменателями.

Очевидно, что ключевым здесь будет навык приведения алгебраических дробей к общему знаменателю. Разберем подробнее.

Приведение алгебраических дробей к общему знаменателю

Чтобы привести алгебраические дроби к общему знаменателю, необходимо осуществить тождественное преобразование заданных дробей, в результате которого знаменатели исходных дробей становятся одинаковыми. Здесь оптимально действовать по следующему алгоритму приведения алгебраических дробей к общему знаменателю:

• сначала определяем общий знаменатель алгебраических дробей;
• затем находим дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели исходных дробей;
• последним действием числители и знаменатели заданных алгебраических дробей умножаются на соответствующие дополнительные множители.

Пример 3

Заданы алгебраические дроби: a + 2 2 · a 3 — 4 · a 2 , a + 3 3 · a 2 — 6 · a и a + 1 4 · a 5 — 16 · a 3 . Необходимо привести их к общему знаменателю.

Решение

Действуем по указанному выше алгоритму. Определим общий знаменатель исходных дробей. С этой целью разложим знаменатели заданных дробей на множители: 2 · a 3 − 4 · a 2 = 2 · a 2 · ( a − 2 ) , 3 · a 2 − 6 · a = 3 · a · ( a − 2 ) и 4 · a 5 − 16 · a 3 = 4 · a 3 · ( a − 2 ) · ( a + 2 ) . Отсюда можем записать общий знаменатель: 12 · a 3 · ( a − 2 ) · ( a + 2 ) .

Теперь нам предстоит найти дополнительные множители. Разделим, согласно алгоритму, найденный общий знаменатель на знаменатели исходных дробей:

• для первой дроби: 12 · a 3 · ( a − 2 ) · ( a + 2 ) : ( 2 · a 2 · ( a − 2 ) ) = 6 · a · ( a + 2 ) ;
• для второй дроби: 12 · a 3 · ( a − 2 ) · ( a + 2 ) : ( 3 · a · ( a − 2 ) ) = 4 · a 2 · ( a + 2 );
• для третьей дроби: 12 · a 3 · ( a − 2 ) · ( a + 2 ) : ( 4 · a 3 · ( a − 2 ) · ( a + 2 ) ) = 3 .

Следующий шаг — умножение числителей и знаменателей заданных дробей на найденные дополнительные множители:

a + 2 2 · a 3 — 4 · a 2 = ( a + 2 ) · 6 · a · ( a + 2 ) ( 2 · a 3 — 4 · a 2 ) · 6 · a · ( a + 2 ) = 6 · a · ( a + 2 ) 2 12 · a 3 · ( a — 2 ) · ( a + 2 ) a + 3 3 · a 2 — 6 · a = ( a + 3 ) · 4 · a 2 · ( a + 2 ) 3 · a 2 — 6 · a · 4 · a 2 · ( a + 2 ) = 4 · a 2 · ( a + 3 ) · ( a + 2 ) 12 · a 3 · ( a — 2 ) · ( a + 2 ) a + 1 4 · a 5 — 16 · a 3 = ( a + 1 ) · 3 ( 4 · a 5 — 16 · a 3 ) · 3 = 3 · ( a + 1 ) 12 · a 3 · ( a — 2 ) · ( a + 2 )

Ответ: a + 2 2 · a 3 — 4 · a 2 = 6 · a · ( a + 2 ) 2 12 · a 3 · ( a — 2 ) · ( a + 2 ) ; a + 3 3 · a 2 — 6 · a = 4 · a 2 · ( a + 3 ) · ( a + 2 ) 12 · a 3 · ( a — 2 ) · ( a + 2 ) ; a + 1 4 · a 5 — 16 · a 3 = 3 · ( a + 1 ) 12 · a 3 · ( a — 2 ) · ( a + 2 ) .

Так, мы привели исходные дроби к общему знаменателю. В случае необходимости далее можно преобразовать полученный результат в вид алгебраических дробей, осуществив умножение многочленов и одночленов в числителях и знаменателях.

Уточним также такой момент: найденный общий знаменатель оптимально оставлять в виде произведения на случай необходимости сократить конечную дробь.

Мы рассмотрели подробно схему приведения исходных алгебраических дробей к общему знаменателю, теперь можем приступить к разбору примеров на сложение и вычитание дробей с разными знаменателями.

Заданы алгебраические дроби: 1 — 2 · x x 2 + x и 2 · x + 5 x 2 + 3 · x + 2 . Необходимо осуществить действие их сложения.

Решение

Исходные дроби имеют разные знаменатели, поэтому первым действием приведем их к общему знаменателю. Раскладываем знаменатели на множители: x 2 + x = x · ( x + 1 ) , а x 2 + 3 · x + 2 = ( x + 1 ) · ( x + 2 ) , т.к. корни квадратного трехчлена x 2 + 3 · x + 2 это числа: — 1 и — 2 . Определяем общий знаменатель: x · ( x + 1 ) · ( x + 2 ) , тогда дополнительные множители будут: x + 2 и – x для первой и второй дробей соответственно.

Таким образом: 1 — 2 · x x 2 + x = 1 — 2 · x x · ( x + 1 ) = ( 1 — 2 · x ) · ( x + 2 ) x · ( x + 1 ) · ( x + 2 ) = x + 2 — 2 · x 2 — 4 · x x · ( x + 1 ) · x + 2 = 2 — 2 · x 2 — 3 · x x · ( x + 1 ) · ( x + 2 ) и 2 · x + 5 x 2 + 3 · x + 2 = 2 · x + 5 ( x + 1 ) · ( x + 2 ) = 2 · x + 5 · x ( x + 1 ) · ( x + 2 ) · x = 2 · x 2 + 5 · x x · ( x + 1 ) · ( x + 2 )

Теперь сложим дроби, которые мы привели к общему знаменателю:

2 — 2 · x 2 — 3 · x x · ( x + 1 ) · ( x + 2 ) + 2 · x 2 + 5 · x x · ( x + 1 ) · ( x + 2 ) = = 2 — 2 · x 2 — 3 · x + 2 · x 2 + 5 · x x · ( x + 1 ) · ( x + 2 ) = 2 · 2 · x x · ( x + 1 ) · ( x + 2 )

Полученную дробь возможно сократить на общий множитель x + 1 :

2 + 2 · x x · ( x + 1 ) · ( x + 2 ) = 2 · ( x + 1 ) x · ( x + 1 ) · ( x + 2 ) = 2 x · ( x + 2 )

И, напоследок, полученный результат запишем в виде алгебраической дроби, заменив произведение в знаменателе многочленом:

2 x · ( x + 2 ) = 2 x 2 + 2 · x

Запишем ход решения кратко в виде цепочки равенств:

1 — 2 · x x 2 + x + 2 · x + 5 x 2 + 3 · x + 2 = 1 — 2 · x x · ( x + 1 ) + 2 · x + 5 ( x + 1 ) · ( x + 2 ) = = 1 — 2 · x · ( x + 2 ) x · x + 1 · x + 2 + 2 · x + 5 · x ( x + 1 ) · ( x + 2 ) · x = 2 — 2 · x 2 — 3 · x x · ( x + 1 ) · ( x + 2 ) + 2 · x 2 + 5 · x x · ( x + 1 ) · ( x + 2 ) = = 2 — 2 · x 2 — 3 · x + 2 · x 2 + 5 · x x · ( x + 1 ) · ( x + 2 ) = 2 · x + 1 x · ( x + 1 ) · ( x + 2 ) = 2 x · ( x + 2 ) = 2 x 2 + 2 · x

Ответ: 1 — 2 · x x 2 + x + 2 · x + 5 x 2 + 3 · x + 2 = 2 x 2 + 2 · x

Обратите внимание еще на такую деталь: перед тем, как алгебраические дроби сложить или вычесть, при наличии возможности их желательно преобразовать с целью упрощения.

Необходимо осуществить вычитание дробей: 2 1 1 3 · x — 2 21 и 3 · x — 1 1 7 — 2 · x .

Решение

Преобразуем исходные алгебраические дроби для упрощения дальнейшего решения. Вынесем за скобки числовые коэффициенты переменных в знаменателе:

2 1 1 3 · x — 2 21 = 2 4 3 · x — 2 21 = 2 4 3 · x — 1 14 и 3 · x — 1 1 7 — 2 · x = 3 · x — 1 — 2 · x — 1 14

Данное преобразование однозначно дало нам пользу: мы явно видим наличие общего множителя.

Избавимся вообще от числовых коэффициентов в знаменателях. Для этого используем основное свойство алгебраических дробей: числитель и знаменатель первой дроби умножим на 3 4 , а второй на — 1 2 , тогда получим:

2 4 3 · x — 1 14 = 3 4 · 2 3 4 · 4 3 · x — 1 14 = 3 2 x — 1 14 и 3 · x — 1 — 2 · x — 1 14 = — 1 2 · 3 · x — 1 — 1 2 · — 2 · x — 1 14 = — 3 2 · x + 1 2 x — 1 14 .

Совершим действие, которое нам позволит избавиться от дробных коэффициентов: умножим полученные дроби на 14 :

3 2 x — 1 14 = 14 · 3 2 14 · x — 1 14 = 21 14 · x — 1 и — 3 2 · x + 1 2 x — 1 14 = 14 · — 3 2 · x + 1 2 x — 1 14 = — 21 · x + 7 14 · x — 1 .

Наконец, выполним требуемое в условии задачи действие – вычитание:

2 1 1 3 · x — 2 21 — 3 · x — 1 1 7 — 2 · x = 21 14 · x — 1 — — 21 · x + 7 14 · x — 1 = 21 — — 21 · x + 7 14 · x — 1 = 21 · x + 14 14 · x — 1

Ответ: 2 1 1 3 · x — 2 21 — 3 · x — 1 1 7 — 2 · x = 21 · x + 14 14 · x — 1 .

Сложение и вычитание алгебраической дроби и многочлена

Данное действие сводится также к сложению или вычитанию алгебраических дробей: необходимо представить исходный многочлен как дробь со знаменателем 1 .

Необходимо произвести сложение многочлена x 2 − 3 с алгебраической дробью 3 · x x + 2 .

Решение

Запишем многочлен как алгебраическую дробь со знаменателем 1 : x 2 — 3 1

Теперь можем выполнить сложение по правилу сложения дробей с разными знаменателями:

x 2 — 3 + 3 · x x + 2 = x 2 — 3 1 + 3 · x x + 2 = x 2 — 3 · ( x + 2 ) 1 · x + 2 + 3 · x x + 2 = = x 3 + 2 · x 2 — 3 · x — 6 x + 2 + 3 · x x + 2 = x 3 + 2 · x 2 — 3 · x — 6 + 3 · x x + 2 = = x 3 + 2 · x 2 — 6 x + 2

Ответ: x 2 — 3 + 3 · x x + 2 = x 3 + 2 · x 2 — 6 x + 2 .

Источник