Растровый способ кодирования это

Урок 9
Кодирование рисунков
§ 12. Кодирование рисунков: растровый метод
§ 13. Кодирование рисунков: другие методы

Содержание урока

§ 12. Кодирование рисунков: растровый метод

Что такое растровое кодирование?

§ 13. Кодирование рисунков: другие методы

§ 12. Кодирование рисунков: растровый метод

Что такое растровое кодирование?

Ключевые слова:

• растр
• пиксель
• разрешение
• цветовая модель RGB
• цветовая модель CMYK
• цветовая модель HSB
• глубина цвета
• цветовая палитра

Рисунок состоит из линий и закрашенных областей. В идеале нам нужно закодировать все особенности этого изображения так, чтобы его можно было в точности восстановить из кода (например, распечатать на принтере).

И линия, и область состоят из бесконечного числа точек. Цвет каждой из этих точек нам нужно как-то закодировать. Так как точек бесконечно много, для этого нужно бесконечно много памяти, поэтому таким способом изображение закодировать не удастся. Однако «поточечную» идею всё-таки можно использовать.

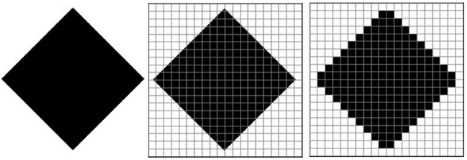
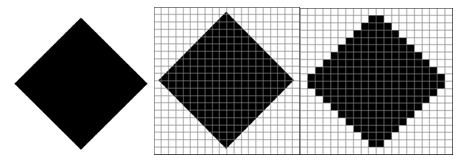
Начнём с чёрно-белого рисунка. Представим себе, что на изображение ромба наложена сетка, которая разбивает его на квадратики. Такая сетка называется растром. Теперь каждый квадратик внутри ромба зальём чёрным цветом, а каждый квадратик вне ромба — белым. Для тех квадратиков, в которых часть оказалась закрашена чёрным цветом, а часть — белым, выберем цвет в зависимости от того, какая часть (чёрная или белая) больше (рис. 2.19).

У нас получился растровый рисунок, состоящий из квадратиков-пикселей.

Пиксель (англ. pixel: picture element — элемент рисунка) — это наименьший элемент рисунка, для которого можно задать свой цвет.

Разбив рисунок на квадратики, мы выполнили его дискретизацию. Действительно, у нас был непрерывный рисунок — изображение ромба. В результате мы получили дискретный объект — набор пикселей.

Двоичный код для чёрно-белого рисунка, полученного в результате дискретизации, можно построить следующим образом:

1) кодируем белые пиксели нулями, а чёрные — единицами 1) ;
2) выписываем строки полученной таблицы одну за другой.

1) Можно сделать и наоборот, чёрные пиксели обозначить нулями, а белые — единицами.

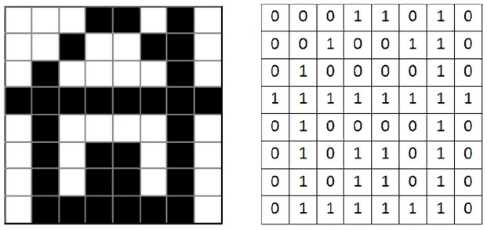
Покажем это на простом примере (рис. 2.20).

Ширина этого рисунка — 8 пикселей, поэтому каждая строка таблицы состоит из 8 двоичных разрядов — битов. Чтобы не писать очень длинную цепочку нулей и единиц, удобно использовать шестнадцатеричную систему счисления, закодировав 4 соседних бита (тетраду) одной шестнадцатеричной цифрой. Например, для первой строки получаем код 1А₁₆:

0	0	0	1	1	0	1	0
1				A

а для всего рисунка: 1A2642FF425A5A7E₁₆.

Используя полученный шестнадцатеричный код картинки, подсчитайте её информационный объём в битах и байтах.

Очень важно понять, что мы приобрели и что потеряли в результате дискретизации. Самое главное — мы смогли закодировать изображение в двоичном коде. Однако при этом рисунок исказился — вместо ромба мы получили набор квадратиков. Причина искажения в том, что в некоторых квадратиках части исходного рисунка были закрашены разными цветами, а в закодированном изображении каждый пиксель обязательно имеет один цвет. Таким образом, часть исходной информации при кодировании была потеряна. Это проявится, например, при увеличении рисунка — квадратики увеличиваются и рисунок ещё больше искажается. Чтобы уменьшить потери информации, нужно уменьшать размер пикселя, т. е. увеличивать разрешение.

Разрешение — это количество пикселей, приходящихся на единицу линейного размера изображения (чаще всего — на 1 дюйм).

Разрешение обычно измеряется в пикселях на дюйм (используется английское обозначение ppi: — pixels per inch). Например, разрешение 254 ppi означает, что на дюйм приходится 254 пикселя.

Чем больше разрешение, тем точнее кодируется рисунок (меньше информации теряется), однако одновременно растёт и объём файла.

Одна и та же картинка была отсканирована дважды: в первый раз с разрешением 300 ppi, а второй раз — с разрешением 600 ppi. Что можно сказать о размерах полученных файлов?

Существуют два основных способа получения растровых изображений:

1) ввод с помощью какого-либо устройства, например сканера, цифрового фотоаппарата или веб-камеры; напомним, что при сканировании происходит преобразование информации в компьютерные данные (оцифровка);

2) создание рисунка с помощью какой-либо программы.

Используя дополнительные источники, найдите ответы на вопросы.

— Чему равен один дюйм в миллиметрах?
— Если отсканировать рисунок с разрешением 254 ppi, какой размер будет иметь изображение одного пикселя?
— Какие размеры в пикселях будет иметь изображение рисунка размером 10 х 15 см, если отсканировать его с разрешением 254 ppi?

Следующая страница Как кодируется цвет?

Cкачать материалы урока

Источник

Информатика. 10 класс

Конспект урока

Информатика, 10 класс. Урок № 17.

Тема — Кодирование графической и звуковой информации

Большую часть информации человек получает с помощью зрения и слуха. Важность этих органов чувств обусловлена развитием человека как биологического вида, поэтому человеческий мозг с большой скоростью способен обрабатывать огромное количество графической и звуковой информации.

С появлением компьютеров возникла огромная потребность научить их обрабатывать такую информацию. Как же такую информацию может обработать компьютер?

Итак, кодирование графической информации осуществляется двумя различными способами: векторным и растровым

Программы, работающие с векторной графикой, хранят информацию об объектах, составляющих изображение в виде графических примитивов: прямых линий, дуг окружностей, прямоугольников, закрасок и т.д.

Достоинства векторной графики:

— Преобразования без искажений.

— Маленький графический файл.

— Рисовать быстро и просто.

— Независимое редактирование частей рисунка.

— Высокая точность прорисовки.

— Редактор быстро выполняет операции.

Недостатки векторной графики:

— Векторные изображения выглядят искусственно.

— Ограниченность в живописных средствах.

Программы растровой графики работают с точками экрана (пикселями). Это называется пространственной дискретизацией.

КОДИРОВАНИЕ РАСТРОВОЙ ГРАФИКИ

Давайте более подробно рассмотрим растровое кодирование информации.

Компьютер запоминает цвет каждой точки, а пользователь из таких точек собирает рисунок.

При этом зная количество пикселей по вертикале и горизонтали, мы сможем найти — разрешающую способность изображения.

Разрешающая способность находится по формуле:

где n, m — количество пикселей в изображении по вертикали и горизонтали.

В процессе дискретизации каждый пиксель может принимать различные цвета из палитры цветов. При этом зная количество цветов, которые можно использовать в палитре и воспользовавшись формулой Хартли, мы сможем найти количество информации, которое используется для кодирования цвета точки, что мы будем называть глубиной цвета.

где N — количество цветов в палитре;

i — глубина цвета.

Таким образом, чтобы найти вес изображения достаточно перемножить разрешающую способность изображения на глубину цвета: L=P*i.

Каким именно образом возможно закодировать пиксель? Для этого используются кодировочные палитры.

КОДИРОВОЧНАЯ ПАЛИТРА RGB

Когда художник рисует картину, цвета он выбирает по своему вкусу. Но цвет в компьютере надо стандартизировать, чтобы его можно было распознать. Поэтому надо определить, что такое каждый цвет.

В экспериментах по производству цветных стекол М. В. Ломоносов показал, что получить любой цвет возможно, используя три различных цвета.

Этот факт был обобщен Германом Грассманом в виде законов аддитивного синтеза цвета.

Давайте рассмотрим два из этих законов:

— Закон трехмерности. С помощью трех независимых цветов можно, смешивая их в однозначно определенной пропорции, выразить любой цвет.

— Закон непрерывности. При непрерывном изменении пропорции, в которой взяты компоненты цветовой смеси, получаемый цвет также меняется непрерывно.

Из биологии вы знаете, что рецепторы человеческого глаза делятся на две группы: палочки и колбочки. Палочки более чувствительны к интенсивности поступаемого света, а колбочки — к длине волны.

Если посмотреть, как распределяется количество колбочек по тому, на какую длину волны они «настроены», то количество колбочек «настроенных» на синий, красный и зеленый цвета окажется больше.

Поэтому такие цвета были взяты основными для построения цветовой модели, которая получила название RGB (Red, Green, Blue). То есть задавая количество любого из этих трех цветов, можно получить любой другой. Для кодирования каждого цвета было выделено 8 бит (режим True-Color). Таким образом, количество каждого цвета может изменяться от 0 до 255, часто это количество выражается в шестнадцатеричной системе счисления (от 0 до FF).

Так как описание цвета происходит определением трех величин, то это наводит на мысль считать их координатами точки в пространстве. Получается, что координаты цветов заполняют куб.

При этом яркость цвета определяется тем насколько близка к максимальному значению хотя бы одна координата из трех.

Поскольку именно модель RGB соответствовала основному механизму формирования цветного изображения на экране, большинство графических файлов хранят изображение именно в этой кодировке. Если же используется другая модель, например в JPEG , то приходится при выводе информации на экран преобразовывать данные.

КОДИРОВАНИЕ ЗВУКОВОЙ ИНФОРМАЦИИ

Давайте перейдем к кодированию звуковой информации.

Из курса физики вам всем известно, что звук — это непрерывная волна с изменяющейся амплитудой и частотой.

Для того, чтобы компьютер мог обрабатывать непрерывный звуковой сигнал, он должен быть дискретизирован, т. е. превращен в последовательность электрических импульсов (двоичных нулей и единиц).

Для этого звуковая волна разбивается на отдельные временные участки.

Гладкая кривая заменяется последовательностью «ступенек». Каждой «ступеньке» присваивается значение громкости звука. Чем больше количество уровней громкости, тем больше количество информации будет нести значение каждого уровня и более качественным будет звучание. Причем, чем больше будет количество измерений уровня звукового сигнала в единицу времени, тем качественнее будет звучание. Эта характеристика называется частотой дискретизации Данная характеристика измеряется в Гц.

При этом на каждое измерение выделяется одинаковое количество бит. Такая характеристика называется — глубина кодирования.

Таким образом, чтобы подсчитать вес звуковой волны достаточно перемножить частоту дискретизации, глубины кодирования и времени звучания такого звука. При этом, рассматривая современное звучание, количество звуковых волн может быть различное, например, для стереозвука — это 2, а для квадрозвука — 4.

Источник

Растровое кодирование

Вы будете перенаправлены на Автор24

Растры, пиксели, дискретизация, разрешение

Как и все виды информации, изображения в компьютере закодированы в виде двоичных последовательностей. Используют два принципиально разных метода кодирования, каждый из которых имеет свои достоинства и недостатки.

И линия, и область состоят из бесконечного числа точек. Цвет каждой из этих точек нам нужно закодировать. Если их бесконечно много, мы сразу приходим к выводу, что для этого нужно бесконечно много памяти. Поэтому «поточечным» способом изображение закодировать не удастся. Однако, эту все-таки идею можно использовать.

Начнем с черно-белого рисунка. Представим себе, что на изображение ромба наложена сетка, которая разбивает его на квадратики. Такая сетка называется растром. Теперь для каждого квадратика определим цвет (черный или белый). Для тех квадратиков, в которых часть оказалась закрашена черным цветом, а часть белым, выберем цвет в зависимости от того, какая часть (черная или белая) больше.

У нас получился так называемый растровый рисунок, состоящий из квадратиков-пикселей.

Пиксель (англ. pixel = picture element, элемент рисунка) – это наименьший элемент рисунка, для которого можно задать свой цвет. Разбив «обычный» рисунок на квадратики, мы выполнили его дискретизацию – разбили единый объект на отдельные элементы. Действительно, у нас был единый и неделимый рисунок – изображение ромба. В результаты мы получили дискретный объект – набор пикселей.

Двоичный код для черно-белого рисунка, полученного в результате дискретизации можно построить следующим образом:

Готовые работы на аналогичную тему

• заменяем белые пиксели нулями, а черные – единицами;
• выписываем строки полученной таблицы одну за другой.

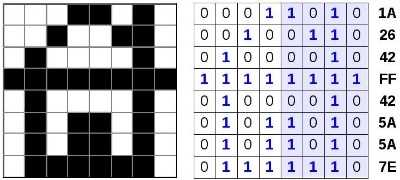
Покажем это на простом примере:

Ширина этого рисунка – $8$ пикселей, поэтому каждая строчка таблицы состоит из $8$ двоичных разрядов – битов. Чтобы не писать очень длинную цепочку нулей и единиц, удобно использовать шестнадцатеричную систему счисления, закодировав $4$ соседних бита (тетраду) одной шестнадцатеричной цифрой.

Например, для первой строки получаем код $1A_<16>$:

а для всего рисунка: $1A2642FF425A5A7E_<16>$.

Очень важно понять, что мы приобрели и что потеряли в результате дискретизации. Самое важное – мы смогли закодировать рисунок в двоичном коде. Однако при этом рисунок исказился — вместо ромба мы получили набор квадратиков. Причина искажения в том, что в некоторых квадратиках части исходного рисунка были закрашены разными цветами, а в закодированном изображении каждый пиксель обязательно имеет один цвет. Таким образом, часть исходной информации при кодировании была потеряна. Это проявится, например, при увеличении рисунка — квадратики увеличиваются, и рисунок еще больше искажается. Чтобы уменьшить потери информации, нужно уменьшать размер пикселя, то есть увеличивать разрешение.

Разрешение – это количество пикселей, приходящихся на дюйм размера изображения.

Разрешение обычно измеряется в пикселях на дюйм (используется английское обозначение $ppi$ = pixels per inch). Например, разрешение $254$ $ppi$ означает, что на дюйм ($25,4$ мм) приходится $254$ пикселя, так что каждый пиксель «содержит» квадрат исходного изображения размером $0,1×0,1$ мм. Чем больше разрешение, тем точнее кодируется рисунок (меньше информации теряется), однако одновременно растет и объем файла.

Кодирование цвета

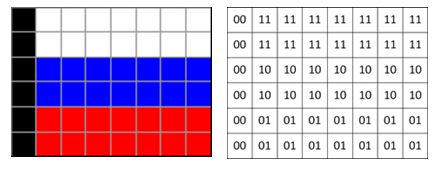
Что делать, если рисунок цветной? В этом случае для кодирования цвета пикселя уже не обойтись одним битом. Например, в показанном на рисунке изображении российского флага $4$ цвета: черный, синий, красный и белый. Для кодирования одного из четырех вариантов нужно $2$ бита, поэтому код каждого цвета (и код каждого пикселя) будет состоять из двух бит. Пусть $00$ обозначает черный цвет, $01$ – красный, $10$ – синий и $11$ – белый. Тогда получаем такую таблицу:

Проблема только в том, что при выводе на экран нужно как-то определить, какой цвет соответствует тому или другому коду. То есть информацию о цвете нужно выразить в виде числа (или набора чисел).

Человек воспринимает свет как множество электромагнитных волн. Определенная длина волны соответствуют некоторому цвету. Например, волны длиной $500-565$ нм – это зеленый цвет. Так называемый «белый» свет на самом деле представляет собой смесь волн, длины которых охватывают весь видимый диапазон.

Согласно современному представлению о цветном зрении (теории Юнга-Гельмгольца), глаз человека содержит чувствительные элементы трех типов. Каждый из них воспринимает весь поток света, но первые наиболее чувствительны в области красного цвета, вторые – области зеленого, а третьи – в области синего цвета. Цвет – это результат возбуждения всех трех типов рецепторов. Поэтому считается, что любой цвет (то есть ощущения человека, воспринимающего волны определенной длины) можно имитировать, используя только три световых луча (красный, зеленый и синий) разной яркости. Следовательно, любой цвет приближенно раскладывается на три составляющих – красную, зеленую и синюю. Меняя силу этих составляющих, можно составить любые цвета. Эта модель цвета получила название RGB по начальным буквам английских слов red (красный), green (зеленый) и blue (синий).

В модели RBG яркость каждой составляющей (или, как говорят, каждого канала) чаще всего кодируется целым числом от $0$ до $255$. При этом код цвета – это тройка чисел (R,G,B), яркости отдельных каналов. Цвет ($0,0,0$) – это черный цвет, а ($255,255,255$) – белый. Если все составляющие имеют равную яркость, получаются оттенки серого цвета, от черного до белого.

Чтобы сделать светло-красный (розовый) цвет, нужно в красном цвете ($255,0,0$) одинаково увеличить яркость зеленого и синего каналов, например, цвет ($255, 150, 150$) – это розовый. Равномерное уменьшение яркости всех каналов делает темный цвет, например, цвет с кодом ($100,0,0$) – тёмно-красный.

Всего есть по $256$ вариантов яркости каждого из трех цветов. Это позволяет закодировать $256^3= 16 777 216$ оттенков, что более чем достаточно для человека. Так как $256 = 2^8$, каждая из трех составляющих занимает в памяти $8$ бит или $1$ байт, а вся информация о каком-то цвете – $24$ бита (или $3$ байта). Эта величина называется глубиной цвета.

Глубина цвета – это количество бит, используемое для кодирования цвета пикселя.

$24$-битное кодирование цвета часто называют режимом истинного цвета (англ. True Color – истинный цвет). Для вычисления объема рисунка в байтах при таком кодировании нужно определить общее количество пикселей (перемножить ширину и высоту) и умножить результат на $3$, так как цвет каждого пикселя кодируется тремя байтами. Например, рисунок размером $20×30$ пикселей, закодированный в режиме истинного цвета, будет занимать $20×30×3 = 1800$ байт.

Кроме режима истинного цвета используется также $16$-битное кодирование (англ. High Color – «высокий» цвет), когда на красную и синюю составляющую отводится по $5$ бит, а на зеленую, к которой человеческий глаз более чувствителен – $6$ бит. В режиме High Color можно закодировать $2^ <16>= 65 536$ различных цветов. В мобильных телефонах $12$-битное кодирование цвета ($4$ бита на канал, $4096$ цветов).

Кодирование с палитрой

Как правило, чем меньше цветов используется, тем больше будет искажаться цветное изображение. Таким образом, при кодировании цвета тоже есть неизбежная потеря информации, которая «добавляется» к потерям, вызванным дискретизацией. Очень часто (например, в схемах, диаграммах и чертежах) количество цветов в изображении невелико (не более $256$). В этом случае применяют кодирование с палитрой.

Цветовая палитра – это таблица, в которой каждому цвету, заданному в виде составляющих в модели RGB, сопоставляется числовой код.

Кодирование с палитрой выполняется следующим образом:

• выбираем количество цветов $N$ (как правило, не более $256$);
• из палитры истинного цвета ($16 777 216$ цветов) выбираем любые $N$ цветов и для каждого из них находим составляющие в модели RGB;
• каждому из цветов присваиваем номер (код) от $0$ до $N–1$;
• составляем палитру, записывая сначала RGB-составляющие цвета, имеющего код $0$, затем составляющие цвета с кодом $1$ и т.д.

Цвет каждого пикселя кодируется не в виде значений RGB-составляющих, а как номер цвета в палитре. Например, при кодировании изображения российского флага (см. выше) были выбраны $4$ цвета:

• черный: RGB-код ($0,0,0$); двоичный код $002$;
• красный: RGB-код ($255,0,0$); двоичный код $012$;
• синий: RGB-код ($0,0,255$); двоичный код $102$;
• белый: RGB-код ($255,255,255$); двоичный код $112$.

Поэтому палитра, которая обычно записывается в специальную служебную область в начале файла (ее называют заголовком файла), представляет собой четыре трехбайтных блока:

Код каждого пикселя занимает всего два бита.

Палитры с количеством цветом более $256$ на практике не используются.

Достоинства и недостатки растрового кодирования

Растровое кодирование имеет достоинства:

• универсальный метод (можно закодировать любое изображение);
• единственный метод для кодирования и обработки размытых изображений, не имеющих четких границ, например, фотографий.

И недостатки:

• при дискретизации всегда есть потеря информации;
• при изменении размеров изображения искажается цвет и форма объектов на рисунке, поскольку при увеличении размеров надо как-то восстановить недостающие пиксели, а при уменьшении – заменить несколько пикселей одним;
• размер файла не зависит от сложности изображения, а определяется только разрешением и глубиной цвета.

Как правило, растровые рисунки имеют большой объем.

Источник