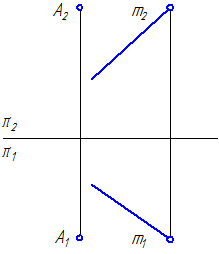Расстояние между ребрами способом замены плоскости проекции

Лекция 4. Способы преобразования ортогонального чертежа

4.1. Способ перемены плоскостей проекций

Чаще всего геометрические объекты расположены относительно плоскостей проекций в общем положении, и при решении задач для достижения поставленной цели необходимо выполнять много построений.

Количество построений можно значительно сократить, если геометрические элементы будут расположены в частном положении относительно плоскостей проекций.

Существуют два основных способа преобразования чертежа, при которых:

1. Объект остаётся неподвижным, при этом меняется аппарат проецирования;
2. Условия проецирования не меняются, но изменяется положение объекта в пространстве.

К первому способу относится способ перемены плоскостей проекций.

Ко второму – способ вращения (вращение вокруг линии уровня и вращение вокруг проецирующей прямой); способ плоскопараллельного перемещения.

Рассмотрим наиболее часто используемые способы при решении задач.

Способ перемены плоскостей проекций или способ введения дополнительных плоскостей проекций (ДПП) позволяет перейти от заданной системы плоскостей проекций к новой системе, более удобной для решения той или иной задачи.

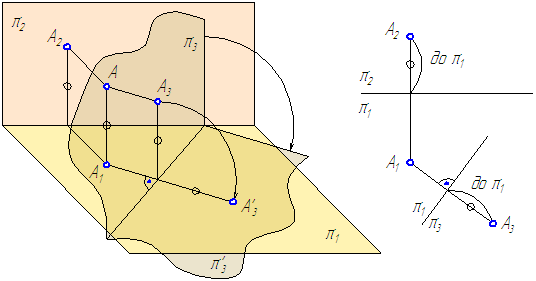
Рассмотрим положение точки А относительно известной системы плоскостей проекций π₂⊥π₁ (Рисунок 4.1, а и б).

Введём π₄⊥π₁, при этом получим новую систему двух взаимно перпендикулярных плоскостей. Положение точки А на эпюре будет в этом случае задано проекциями А₁ и А₄.

Правила перемены плоскостей проекций:

1. Новая плоскость проекций вводится перпендикулярно, по крайней мере, одной из заданных на чертеже плоскостей проекций;
2. ДПП располагается относительно проецируемого объекта в частном положении, удобном для решения поставленной задачи;
3. Новую плоскость совмещаем вращением вокруг новой оси проекций с плоскостью, которой она перпендикулярна на свободное место так, чтобы проекции не накладывались друг на друга.

а б

Рисунок 4.1 – Способ перемены плоскостей проекций

1. На чертеже новая проекция геометрического элемента находится на линии связи, перпендикулярной новой оси проекций:

1. Расстояние от А₄ до π₁/π₄ равно расстоянию от А₂ до π₂/π₁, так как величина этих отрезков (отмечены ○) определяет расстояние от точки А до плоскости проекций π₁.

При решении задачи необходимо заранее обдумать, как расположить новую плоскость проекций относительно заданных геометрических объектов (прямой, плоскости и др.), и как на чертеже провести новую ось проекций, чтобы в новой системе плоскостей заданные объекты заняли бы частные положения по отношению к новой плоскости проекций.

Упражнение

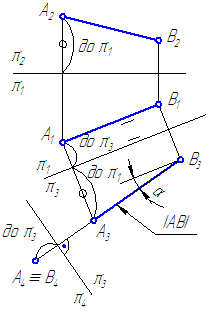
1. Спроецировать отрезок общего положения АВ в точку.

1. Введём ДПП π₄//А₁В₁ и π₄⊥π₁ (Рисунок 4.2). В новой системе двух взаимно перпендикулярных плоскостей проекций π₁/π₄ отрезок АВспроецируется на π₄ в натуральную величину и по этой проекции можем определить угол наклона отрезка к плоскости проекций π₁

Упражнение

2. Дана плоскость общего положения – σ, заданная треугольником АВС (Рисунок 4.3).

Определить истинную величину треугольника.

1. Введём ДПП π₄⊥σ и π₄⊥π₁, для чего построим горизонталь в плоскости треугольника и проведём новую ось проекций π₁/π₄⊥g₁согласно теореме о перпендикуляре к плоскости. На π₄ плоскость σ спроецируется в прямую, что означает σ⊥πp₄.
2. Введём ДПП π₅//σ (π₄/π₅//А₄В₄С₄) и π₄⊥π₅. На π₅ проекция А₅В₅С₅ – есть истинная величина треугольника.

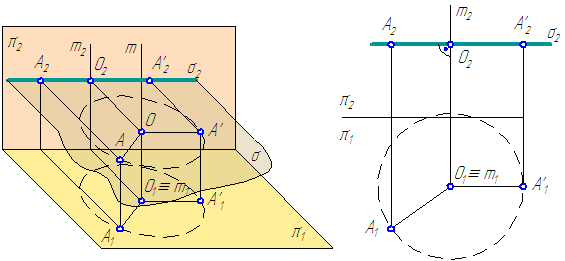
4.2. Способ вращения

Сущность способа вращения состоит в том, что положение системы плоскостей проекций считается неизменным в пространстве, а положение проецируемого объекта относительно неподвижных плоскостей изменяется.

Из сравнения сущности обоих способов видно, что решение задач, которые требуют применения преобразования ортогонального чертежа, может быть выполнено любым из этих способов, результат при этом должен получиться одинаковым. Основа выбора того или иного способа – рациональность решения.

Вращение заданных элементов будем осуществлять вокруг проецирующей прямой, то есть прямой, перпендикулярной какой-либо плоскости проекций, при этом все точки заданных элементов поворачиваются в одну и ту же сторону на один и тот же угол (Рисунок 4.4, а и б). Ось вращения и объект вращения составляют твёрдое тело.

А – точка в пространстве;

О – центр вращения точки А;

АО – радиус вращения

а б

Рисунок 4.4 – Способ вращения вокруг прямой, перпендикулярной π₂

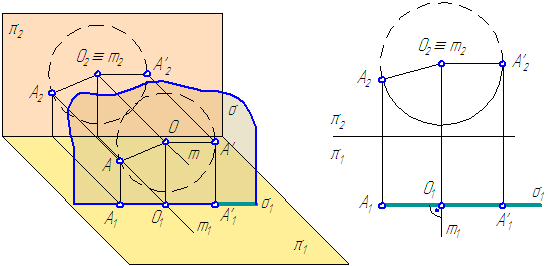
Точка описывает в пространстве окружность радиусом АО. Плоскость окружности перпендикулярна оси вращения (σ⊥m).

Так как m⊥π₂ , то σ//π₂, следовательно, σ⊥π₁, ⇒ σ₁⊥m₁, и поэтому σ проецируется на π₁ в виде прямой, перпендикулярной проекции оси вращения, а на π₂ траектория вращающейся точки проецируется в виде окружности с центром О₂≡m₂.

Пусть ось вращения m⊥π₁ (Рисунок 4.5, а и б). Плоскость окружности σ⊥m.

а б
Рисунок 4.5 – Вращение вокруг прямой, перпендикулярной π₁
\left.\begin\sigma\parallel\pi_1\\\sigma\perp \pi_2\\\end\right\> npu\;m\perp\pi_1\Longrightarrow\sigma_2\perp m_2
Свойства проекций

1. На плоскость проекций, перпендикулярную оси вращения, траектория вращающейся вокруг этой оси точки проецируется без искажения, то есть в окружность с центром, совпадающим с проекцией оси вращения на эту плоскость и радиусом, равным расстоянию от вращаемой точки до оси вращения.
2. На плоскость проекций, параллельную оси вращения, траектория вращающейся точки проецируется в отрезок, перпендикулярный проекции оси вращения на эту плоскость.
3. На плоскость проекций, перпендикулярную оси вращения, проекция вращаемого объекта своих размеров и формы не меняет.

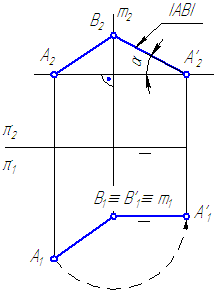
Упражнение

Дано : отрезок общего положения – АВ.

Определить : способом вращения истинную величину отрезка и углы наклона его к плоскостям проекций.

1. Выберем ось вращения m⊥π₁ и проходящую через точку В (Рисунок 4.6).

На плоскости проекций π₂ проекция траектории перемещения точки А – прямая,

A_2 \overline\perp m_2\;u\;A_2\overline\parallel\pi_2/\pi_1

На плоскости проекций π₁ проекция траектории перемещения точки А – окружность радиусом |А₁В₁|.

Повернем отрезок до положения, параллельного плоскости проекций π₂. Получим натуральную величину отрезка.

Угол наклона отрезка АВ к плоскости проекций π₁ будет угол
\alpha=\angle\widehat_2> .

Для того, чтобы определить угол наклона АВ к плоскости проекций π₂, надо ввести новую ось вращения перпендикулярно π₂ и повторить построения.

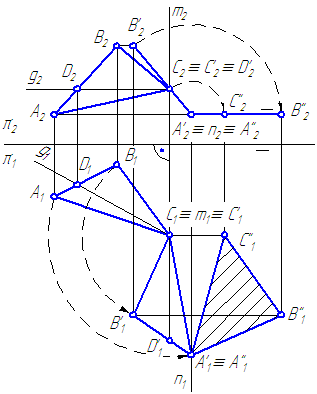
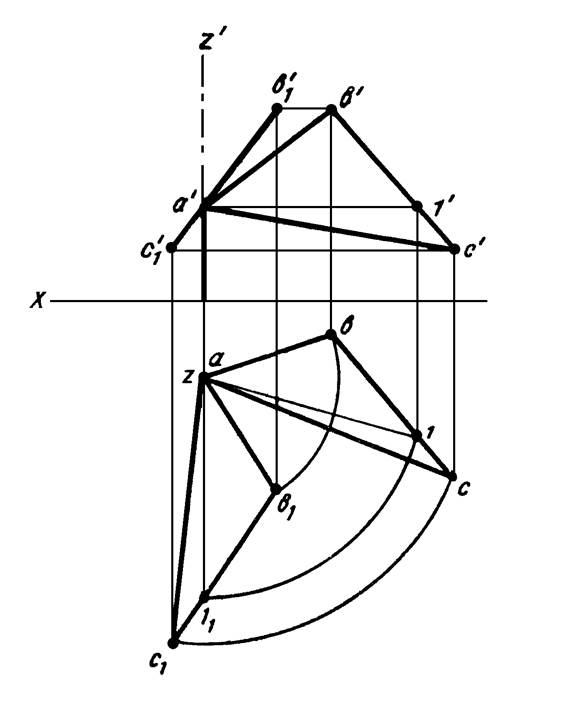
4.3. Определение истинной величины треугольника способом вращения

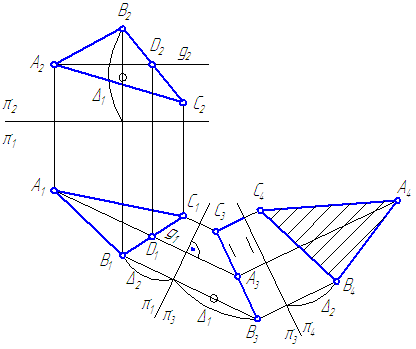
Пусть плоскость σ задана треугольником. Необходимо определить истинную величину треугольника (Рисунок 4.7).

Одним поворотом вокруг оси, перпендикулярной к плоскости проекций, истинную форму треугольника получить нельзя (так же как и введением одной ДПП).

Вращая вокруг оси m, перпендикулярной π₁ можно расположить плоскость ΔАВС⊥π₂ (а вращая вокруг оси n⊥π₂ можно расположить плоскость ΔАВС⊥π₁).

Рисунок 4.7

1. Положим σ’ должна быть перпендикулярна π₂. Для чего построим CD – горизонталь h плоскости σ. Введём первую ось вращения m⊥π₁, например, через точку С.
2. Повернём треугольник вокруг m до положения, когда
   \overline\perp\pi_2\Rightarrow\overline_1\overline_1\perp\pi_2/\pi_1
   На основании 3-го свойства, новая горизонтальная проекция треугольника \overline по величине должна равняться A₁B₁C₁, а фронтальная проекция треугольника будет представлять отрезок.
3. Введём вторую ось вращения n⊥π₂ через точку \overline_2 . Повернём фронтальную проекцию \overline в новое положение \overline<\overline\overline\overline>\parallel\pi_2/\pi_1 . На π₁ получим треугольник \overline<\overline\overline\overline> , равный истинной величине треугольника АВС.

4.4. Задачи для самостоятельной работы

Двумя способами преобразования ортогонального чертежа:

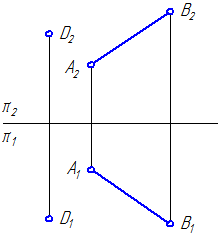
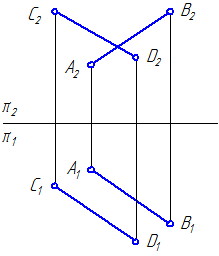
1. Определить расстояние от точки D до отрезка АВ – общего положения (Рисунок 4.8).

Рисунок 4.8

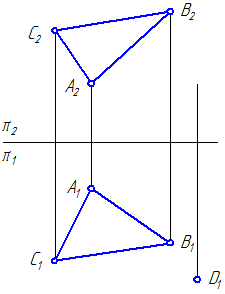
2. Определить расстояние между двумя параллельными прямыми общего положения (АВ//CD) (Рисунок 4.9).

Рисунок 4.9

3. Определить расстояние между двумя скрещивающимися прямыми, заданными отрезками АВ и CD (Рисунок 4.10).

Рисунок 4.10

4. Построить недостающую проекцию точки D при условии, что задана σ=ΔАВС – общего положения и первая проекция точки D₁, Dотстоит от плоскости σ на 30 мм (Рисунок 4.11).

Рисунок 4.11

5. Дан отрезок АВ – общего положения. Ось вращения не проходит через АВ (Рисунок 4.12). Определить способом вращения истинную величину АВ.

Рисунок 4.12

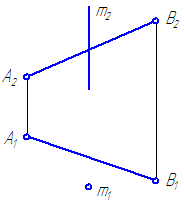
6. Задана прямая общего положения m и точка А вне прямой. Построить плоскость, проходящую через точку А и перпендикулярную прямой m (Рисунок 4.13).

Рисунок 4.13

Источник

Способы преобразования чертежа: Способ замены плоскостей проекций, Способы вращения: Методические рекомендации для самостоятельной работы студентов , страница 2

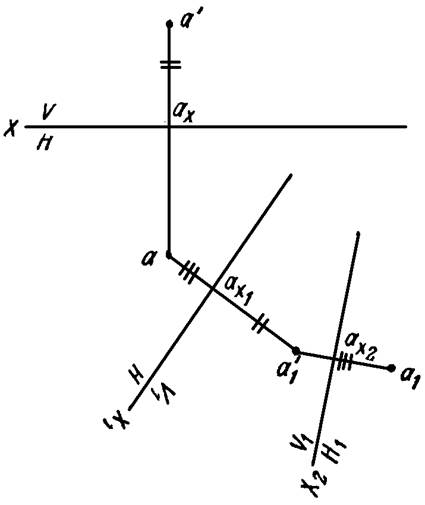
Часто для приведения прямой, плоской фигуры или пространственной формы в то частное положение, которое требуется для решения задачи, приходится заменять обе плоскости проекций. Переход от заданной системы плоскостей V/H к новой V₁/H₁ может быть осуществлен по одной из приведенных ниже схем:

На рисунке 12 задана точка A в системе V/H. Затем осуществлен переход от системы V/H к системе V₁/H₁: проведена новая ось проекций Х₁, найдена новая проекция а’₁ точки А. Далее система V₁/H заменена новой системой плоскостей проекции V₁/H₁ —вместо горизонтальной плоскости проекций введена новая плоскость Н₁.

Положение новых осей проекций выбирается в соответствии с конкретными условиями задачи.

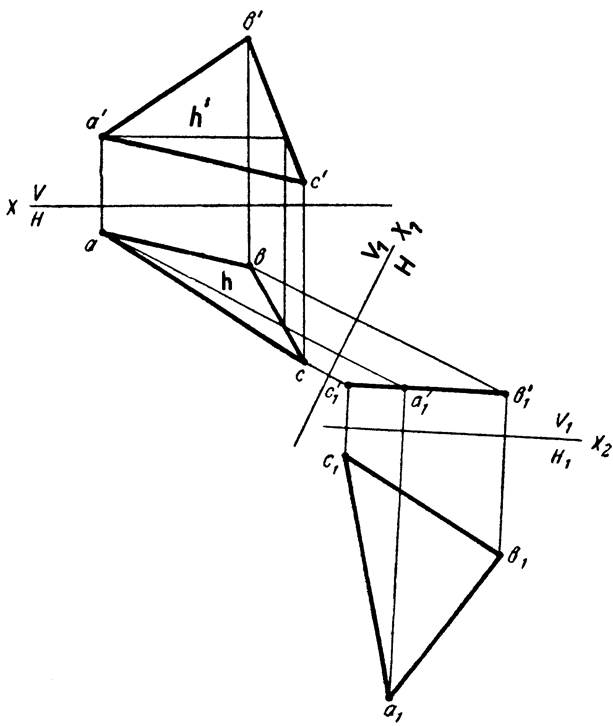
Пример 6. Определить истинную фигуру треугольника ABC (рисунок 13).

Треугольник спроектируется в натуральную величину на какую-либо плоскость проекций, если он окажется параллельным этой плоскости. Для того чтобы треугольник АВС оказался параллельным одной из плоскостей проекций, необходимо выполнить двойную замену плоскостей.

Сначала заменим плоскость V на плоскость V₁. Плоскость V₁ выберем перпендикулярно плоскости треугольника АВС — новая ось проекций x₁должна быть перпендикулярна горизонтальной проекции горизонтали h. На новую фронтальную плоскость проекций треугольник cпроектируетcя в виде прямой линии c’₁a’₁b’₁. Затем введем новую плоскость проекций H₁ параллельно плоскости треугольника.

Горизонтальная проекция a₁b₁c₁ треугольника ABC в новой системе — истинная величина его.

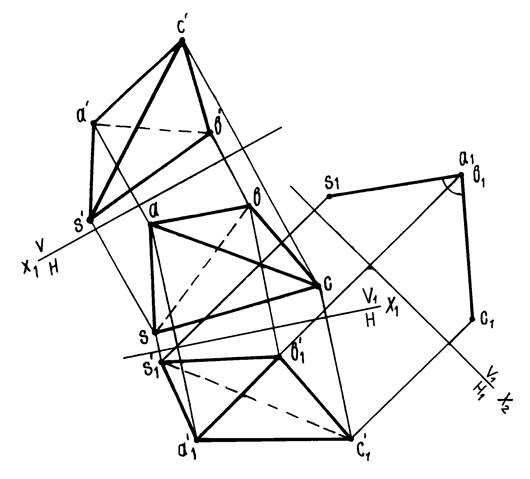
Пример 7. Дана пирамида SАВС (рисунок 14). Определить величину двугранного угла при ребре АВ.

Задача сводится к построению проекции данного угла на плоскость проекций, перпендикулярную к его ребру.

Так как ребро АВ — прямая общего положения, то необходимо произвести две последовательные замены плоскостей проекций. Плоскость V заменяем плоскостью V₁, параллельной отрезку АВ.

Находим новую фронтальную проекцию s’₁a’₁b’₁c’₁ пирамиды SАВС на новой фронтальной плоскости проекций. Затем от системы V₁/H перейдем к системе V₁/H₁. Плоскость H₁ расположим перпендикулярно отрезку АВ. На плоскость Н₁ ребро АВ спроектируется в точку, а грани SАВ и САВ — в прямые. Угол s₁a₁c₁ будет искомым.

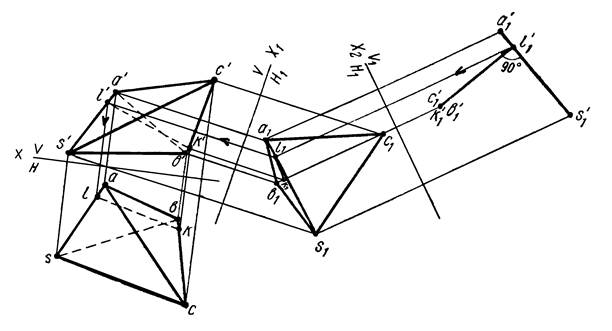
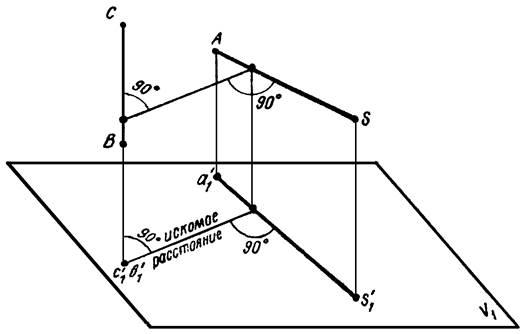
Пример 8. Дана пирамида SАВС (рисунок 15). Определить кратчайшее расстояние между ребрами SА и ВС.

Прямые SА и ВС являются скрещивающимися. Следовательно, задача сводится к определению кратчайшего расстояния между двумя скрещивающимися прямыми. Для решения задачи необходимо произвести такую замену плоскостей проекций, чтобы в новой системе одна из прямых, например ВС (рисунок 16), оказалась перпендикулярной к какой-либо плоскости проекций. Замену плоскостей проекций осуществляем по схеме V/H → V/H₁ → V₁/H₁.

Следовательно, решение задач методами преобразования сводится к выполнению четырех основных этапов:

1) преобразование прямой общего положения в прямую уровня (определение углов наклона прямой к плоскостям проекций и натуральной величины отрезков);

2. преобразование прямой уровня в проецирующую прямую (определение величины двугранного угла, расстояния между прямыми);

3. преобразование плоскости общего положения в проецирующую плоскость (определение углов наклона плоскости к плоскостям проекций, расстояния от точки до плоскости);

4. преобразование плоскости проецирующей в плоскость уровня (определяется натуральная величина плоскости).

В системе V₁H₁ прямая ВС (см. рисунок 15) проектируется в точку. Отрезок k’₁l’₁ — кратчайшее расстояние между ребрами АS и ВС. Для построения проекций кратчайшего расстояния в системе V/H находим по линии связи точку l₁ и проводим l₁k₁ параллельно оси проекций Х₂ , после чего при помощи линий связи находим основные проекции kl и k’l’.

Сущность способов вращения заключается в том, что заданная геометрическая форма путем вращения вокруг некоторой оси перемещается в пространстве до тех пор, пока она не займет частное положение по отношению к неизменной системе плоскостей проекций.

В зависимости от положения оси вращения по отношению к плоскостям проекций различают следующие способы вращения:

а) вращение вокруг осей, перпендикулярных к плоскостям проекций;

б) то же без указания положения осей вращения;

в) вращение вокруг горизонтали или фронтали;

г) вращение вокруг одного из следов плоскости (совмещение).

Рисунок 17 Рисунок 18

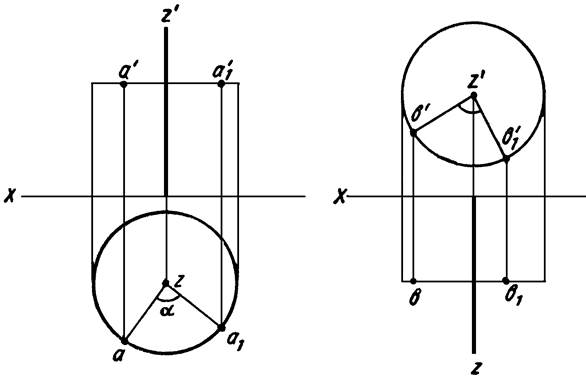
На эпюре (рисунок 17) изображена точка А и ось вращения Z, перпендикулярная к плоскости проекций H. При вращении вокруг оси Z точка А будет перемещаться по окружности, лежащей в плоскости, перпендикулярной оси вращения (параллельной плоскости проекций H). Если точку А переместить из положения А в положение A₁ т. е. повернуть ее вокруг оси Z, на некоторый угол α , то ее горизонтальная проекция (а) займет положение a₁, описав при этом дугу радиуса za (za — радиус вращения), а фронтальная проекция (а’) точки переместится по прямой a’a’₁, параллельной оси X.

Если ось вращения Z (рисунок 18) перпендикулярна к плоскости проекций V, то при вращении точки В вокруг этой оси фронтальная проекция траектории её перемещения будет окружностью, а горизонтальная — прямой, параллельной оси X.

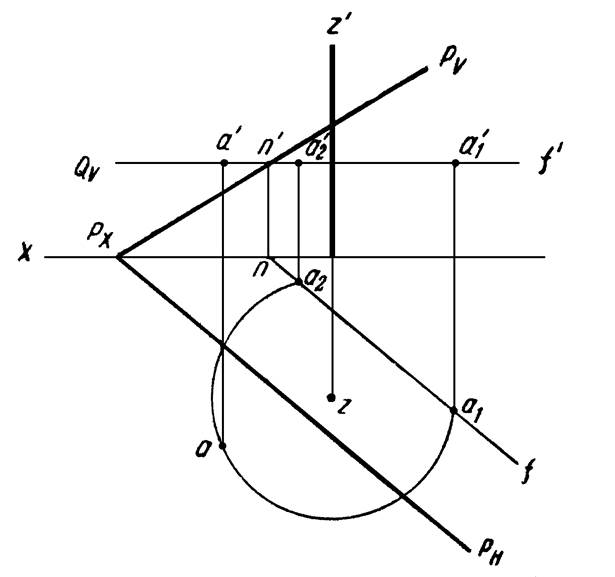
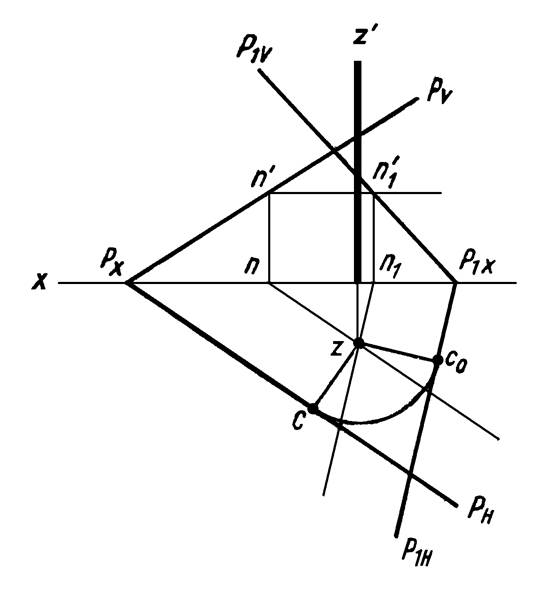
Пример 9. Совместить точку А с плоскостью Р путем вращения ее вокруг заданной оси Z (рисунок 19).

При вращении вокруг оси Z, точка А опишет окружность в плоскости Q, перпендикулярной этой оси. Плоскость Q пересечет заданную плоскость Р по горизонтали NF. Очевидно, точка А окажется в плоскости Р тогда, когда окружность, описываемая точкой А, пересечет горизонталь NF. Задача, как видно из чертежа, имеет два решения.

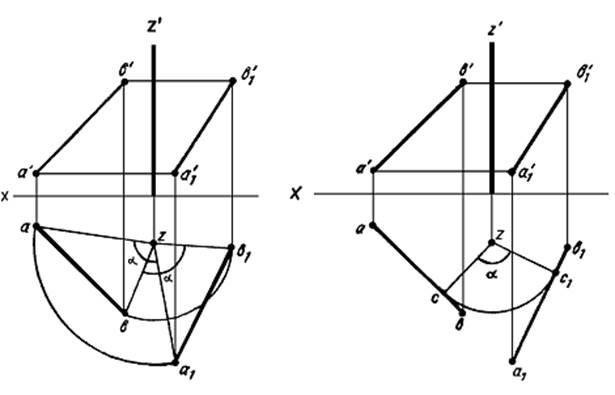
Чтобы повернуть прямую АВ (рисунок 20) на некоторый угол α, достаточно повернуть на заданный угол две принадлежащие, ей точки. Из чертежа видно, что треугольники abz и a₁b₁z₁ равны между собой (по двум сторонам и углу между ними), а из их равенства следует, что ab = a₁b₁, т. е. величина горизонтальной проекции отрезка при вращении его вокруг оси, перпендикулярной Н, не изменяется, изменяется только ее положение относительно оси проекций. Это обстоятельство позволяет упростить построения при решении приведенного примера

Рисунок 20 Рисунок 21

На рисунке 21 для поворота прямой АВ вокруг оси Z на угол α из z, опущен перпендикуляр на ab. Затем точка с повернута на заданный угол α, через точку c₁ проведена прямая, перпендикулярная радиусу c₁z, и отложены отрезки c₁a₁=са и c₁b₁=cb.

Вращение плоскости вокруг оси, перпендикулярной плоскости проекций, осуществляется путем вращения на один и тот же угол в одном и том же направлении точек и прямых, которыми задана плоскость.

На рисунке 22 плоскость, заданная треугольником АВС, повернута вокруг оси Z. в положение, перпендикулярное фронтальной плоскости проекций (горизонтальная проекция горизонтали А1 заняла положение, перпендикулярное оси X).

Если же плоскость задана следами, то для поворота плоскости на некоторый угол необходимо повернуть на заданный угол один из ее следов и горизонталь или фронталь этой плоскости (рисунок 23).

Таким образом, при вращении любой пространственной формы около оси, перпендикулярной одной из плоскостей проекций, проекция ее на эту плоскость по своей величине не изменится. Изменится лишь положение этой проекции относительно оси проекций. Пользуясь этим, для решения той или иной задачи можно применять способ вращения, не изображая на чертеже осей вращения.

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Источник