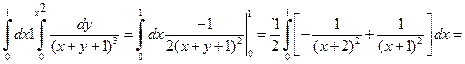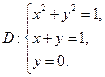Расставьте пределы интегрирования двумя способами для двойного интеграла

РАССТАНОВКА ПРЕДЕЛОВ ИНТЕГРИРОВАНИЯ

1.3.1. Прямоугольная область интегрирования

При сведении двойных интегралов к повторным, основная трудность возникает при расстановке пределов во внутренних интегралах. Наиболее просто это сделать для прямоугольных областей (см. рис. 1.5).

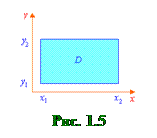
Пример 1.2. Вычислить двойной интеграл

.

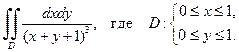
Решение. Запишем двойной интеграл в виде повторного:

.

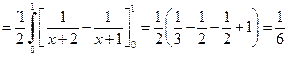
1.3.2. Произвольная область интегрирования

Для того, чтобы перейти от двойного интеграла к повторному следует:

1) построить область интегрирования;

2) расставить пределы в интегралах, при этом следует помнить, что пределы внешнего интеграла должны быть постоянными величинами (т.е. числами) независимо от того, по какой переменной вычисляется внешний интеграл.

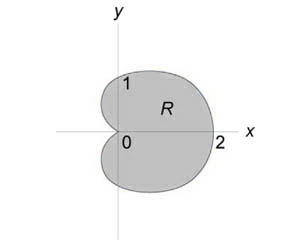
Пример 1.3. Расставить пределы интегрирования в соответствующих повторных интегралах для двойного интеграла

, если а) б)

Решение. а) Изобразим область интегрирования D (см. рис.1.6). Пусть интегрирование во внешнем интеграле производится по переменной x, а во внутреннем – по y. Расстановку пределов всегда нужно начинать с внешнего интеграла, в данном случае с переменной x. Из рисунка видно, что x изменяется от 0 до 1, при этом значения переменной y будут изменяться от значений на прямой y=x до значений на прямой y=2x. Таким образом, получаем

.

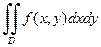
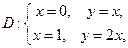
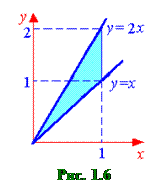
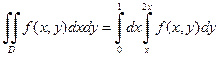
Пусть теперь интегрирование во внешнем интеграле производится по y, а во внутреннем – по x. В этом случае значения y будут изменяться от 0 до 2. Однако тогда верхняя граница изменений значений переменной x будет состоять из двух участков x=y/2 и x=1. Это означает, что область интегрирования нужно разбить на две части прямой y=1. Тогда в первой области y изменяется от 0 до 1, а x от прямой x=y/2 до прямой x=y. Во второй области y изменяется от 1 до 2, а x – от прямой x=y/2 до прямой x=1. В результате получим

.

б) Построим область интегрирования D (см. рис.1.7). Пусть во внешнем интеграле интегрирование производится по x, а во внутреннем – по y. В этом случае при изменении x от –1 до 1 изменения переменной y сверху будут ограничены двумя линиями: окружностью и прямой. На отрезке [–1;0] y изменяется от y=0 до ; на отрезке [0;1] переменная y изменяется от y=0 до y=1–x. Таким образом,

.

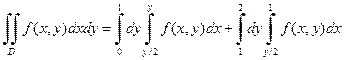
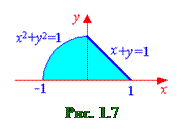
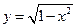
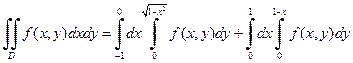
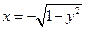
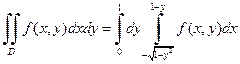
Пусть теперь во внешнем интеграле интегрирование производится по y, а во внутреннем – по x. В этом случае y будет изменяться от 0 до 1, а переменная x – от дуги окружности до прямой x=1–y. В результате получим

.

Данные примеры показывают, как важно правильно выбирать порядок интегрирования.

Пример 1.4. Изменить порядок интегрирования

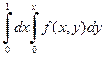
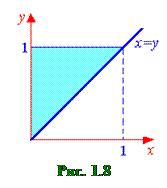
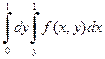
а) ; б) .

Решение. а) Построим область интегрирования. На отрезке [0;1] для x переменная y изменяется от прямой y=0 до прямой y=x. В результате получается следующая область интегрирования (см. рис.1.8). На основании построенного рисунка, расставляем пределы интегрирования

.

б) Построим область интегрирования. На отрезке [0;9/16] для y переменная x изменяется от прямой x=y до параболы 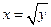; на отрезке [9/16;3/4] – от прямой x=y до прямой x=3/4. В результате получается следующая область интегрирования (см. рис.1.9). На основании построенного рисунка, расставляем пределы интегрирования,

.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

1. Услуги проектирования
2. Двойной интеграл
3. Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Переход от двойного интеграла к повторному. Изменение порядка интегрирования. Переход к полярным координатам

Смысл этих задач — научиться быстро определять параметры $a,\;b,\;\varphi _1 (x),\;\varphi _2 (x),\;c,\;d,\;\psi _1 (y),\;\psi _2 (y)$ < в декартовых координатах >и $\varphi _0 ,\;\varphi _2 ,\;r_1 (\varphi ),\;r_2 (\varphi )$ < в полярных координатах >, необходимые для перехода от двойного интеграла к повторному.

Примеры:

Пусть область $D=\left[< x\leqslant 0,\;y\leqslant 0,\;x^2+y^2\leqslant 4 >\right]\cup \left[< x\geqslant 0,\;x^2+y^2\leqslant -2y >\right]$. Представить двойной интеграл по области $\mathbf < \textit < D >> $ в виде повторных. Перейти к полярным координатам. 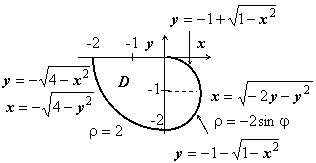Решение:

Область изображена на рисунке. Для левой части $D-2\leqslant x\leqslant 0;\quad -\sqrt < 4-x^2 >\leqslant y\leqslant 0$; для правой — $0\leqslant x\leqslant 1,\;-1-\sqrt < 1-x^2 >\leqslant y\leqslant -1+\sqrt < 1-x^2 >$ уравнение правой полуокружности после выделения полных квадратов принимает вид $x^2+(y+1)^2=1$, поэтому

Изменить порядок интегрирования, перейти к полярным координатам. 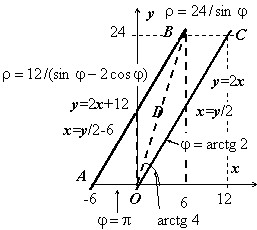$I=\int\limits_ < -6 >^0 < dx\int\limits_0^ < 2x+12 > < f(x,y)dy >> +\int\limits_0^6 < dx\int\limits_ < 2x >^ < 2x+12 > < f(x,y)dy >> +\int\limits_6^ < 12 > < dx\int\limits_ < 2x >^ < 24 > < f(x,y)dy >> $

Решение:

На рисунке изображена область и приведены уравнения прямых и обратных функций для линий, ограничивающих её. $\mathbf < \textit < D >> $ можно представить в виде $D=\left[< 0\leqslant y\leqslant 24,\;y/2-6\leqslant x\leqslant y/2 >\right]$, поэтому $I=\int\limits_0^ < 24 > < dy\int\limits_ < y/2-6 >^ < y/2 > < f(x,y)dx >> $. В полярных координатах $\mathbf < \textit < D >> $ представляется как объединение двух треугольников $\mathbf < \textit < OCB >> $и $\mathbf < \textit < OBA >> $. Уравнение прямой $\mathbf < \textit < ОС >> $: $\varphi =arctg2$ < можно получить и формально, перейдя к полярным координатам в её уравнении: $y=2x\Rightarrow \quad r\sin \varphi =2r\cos \varphi \Rightarrow tg\varphi =2$ >, прямой $\mathbf < \textit < ОВ >> $: $\varphi =arctg4$, прямой $\mathbf < \textit < СВ >> $: $y=24\Rightarrow r\sin \varphi =24\Rightarrow \quad r=24/\sin \varphi $, прямой $\mathbf < \textit < ОА >> $: $\varphi =\pi $, прямой $\mathbf < \textit < АВ >> $: $y=2x+12\Rightarrow r\sin \varphi =2r\cos \varphi +12\Rightarrow \quad r=\frac < 12 > < \sin \varphi -2\cos \varphi >$.

Вычислить двойной интеграл $\iint\limits_ < D > < \left( 6x < < y >^ < 2 >> -12 < < x >^ < 2 >> y \right)dxdy > $, где область $D$ – квадрат со сторонами $x=0$, $x=1$, $y=2$, $y=3$. В повторном интеграле внутренний интеграл вначале вычислить по переменной $y$, а внешний – по $x$. Вычислить этот же интеграл, изменив порядок интегрирования.

Решение:

Вначале изобразим область интегрирования. Запишем заданный двойной интеграл через повторные: $\iint\limits_ < D > < \left( 6x < < y >^ < 2 >> -12 < < x >^ < 2 >> y \right)dxdy > =\int\limits_ < 0 >^ < 1 > < dx >\int\limits_ < 2 >^ < 3 > < \left( 6x < < y >^ < 2 >> -12 < < x >^ < 2 >> y \right)dy > $.

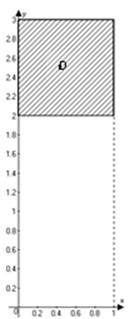
Внутреннее < первое >интегрирование будем выполнять по переменной $y$ < при этом считаем, что $x$ – константа >, а внешнее < второе >– по переменной $x$:

$$=\int\limits_ < 0 >^ < 1 > < 38xdx >-\int\limits_ < 0 >^ < 1 > < 30 < < x >^ < 2 >> dx > =38\int\limits_ < 0 >^ < 1 > < xdx >-30\int\limits_ < 0 >^ < 1 > < < < x >^ < 2 >> dx > =38\cdot \left. \frac < < < x >^ < 2 >> > < 2 >\right|_ < 0 >^ < 1 >-30\cdot \left. \frac < < < x >^ < 3 >> > < 3 >\right|_ < 0 >^ < 1 >=$$

Вычислим теперь заданный по условию двойной интеграл, сменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$ < считая, что $y$ есть постоянной >, а внешнее – по переменной $y$:

$$=\int\limits_ < 2 >^ < 3 > < \left[ 6 < < y >^ < 2 >> \int\limits_ < 0 >^ < 1 > < xdx >-12y\int\limits_ < 0 >^ < 1 > < < < x >^ < 2 >> dx >\right]dy > =\int\limits_ < 2 >^ < 3 > < \left[ 6 < < y >^ < 2 >> \cdot \left. \frac < < < x >^ < 2 >> > < 2 >\right|_ < 0 >^ < 1 >-12y\cdot \left. \frac < < < x >^ < 3 >> > < 3 >\right|_ < 0 >^ < 1 >\right]dy > =$$

$$=\int\limits_ < 2 >^ < 3 > < \left( 3 < < y >^ < 2 >> -4y \right)dy > =\left. \left( 3\cdot \frac < < < y >^ < 3 >> > < 3 >-4\cdot \frac < < < y >^ < 2 >> > < 2 >\right) \right|_ < 2 >^ < 3 >=27-8-2\left( 9-4 \right)=19-10=9$$

Вычислить двойной интеграл $\iint\limits_ < D > < \left( < < x >^ < 2 >> +2y \right)dxdy > $, если область $D$ ограничена линиями $y= < < x >^ < 2 >> $, $x=2$, $y=2x-1$. Вычислить этот же интеграл, изменив порядок интегрирования.

Решение:

Строим заданную область $D$. Вначале внутреннее интегрирование будем проводить по переменной $y$, а внешнее – по $x$: $$\iint\limits_ < D > < \left( < < x >^ < 2 >> +2y \right)dxdy > =\int\limits_ < a >^ < b > < dx >\int\limits_ < < < \phi >_ < 1 >> \left( x \right) > ^ < < < \phi >_ < 2 >> \left( x \right) > < \left( < < x >^ < 2 >> +2y \right)dy > $$

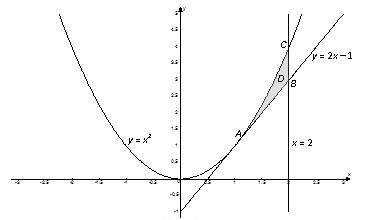
Контур области $D$ пересекается любой прямой, параллельной оси ординат, в двух точках.

Найдем пределы интегрирования. Переменная $x$ изменяется от абсциссы точки $A$ к абсциссе точек $B$ и $C$. Координаты точки $A$ найдем как координаты точки пересечения графиков функций $y= < < x >^ < 2 >> $ и $y=2x-1$:

$$\left[ \begin < matrix >y= < < x >^ < 2 >> , \\ y=2x-1 \\ \end < matrix >\right.\Rightarrow < < x >^ < 2 >> =2x-1\Rightarrow < < x >^ < 2 >> -2x+1=0\Rightarrow < < \left( x-1 \right) >^ < 2 >> =0\Rightarrow < < x >_ < A >> =1$$

Так как точки $B$ и $C$ лежать на прямой $x=2$, то $ < < x >_ < B >> = < < x >_ < C >> =2$. Итак, $1\le x\le 2$. Далее на отрезке $\left[ 1;\ 2 \right]$ выбираем произвольную точку $x$, через нее проводим прямую, параллельную оси $Oy$, и на этой прямой рассмотрим отрезок $KL$, принадлежащий области $D$.

Область $D$ ограничена снизу прямой $y=2x-1$, а сверху – веткой параболы $y= < < x >^ < 2 >> $. Переменная $y$ изменяется в заданной области $D$ от ее значения $2x-1$ на нижней части контура $ABC$ до ее значения $ < < x >^ < 2 >> $ на верхней части этого контура.

Замечание. Уравнения линий, ограничивающих контур, должны быть разрешены относительно той переменной, относительно которой находится внутренний интеграл.

Таким образом, $2x-1\le y\le < < x >^ < 2 >> $, а тогда область $D$ задается следующими неравенствами:

$$D:\left[ \begin < matrix >1\le x\le 2, \\ 2x-1\le y\le < < x >^ < 2 >> . \\ \end < matrix >\right.$$

Вычислим теперь рассматриваемый двойной интеграл, изменив порядок интегрирования: внутреннее интегрирование будем проводить по переменной $x$, а внешнее – по $y$. То есть, перейдя к повторным интегралам, получим:

$$\iint\limits_ < D > < \left( < < x >^ < 2 >> +2y \right)dxdy > =\int\limits_ < c >^ < d > < dy >\int\limits_ < < < \psi >_ < 1 >> \left( y \right) > ^ < < < \psi >_ < 2 >> \left( y \right) > < \left( < < x >^ < 2 >> +2y \right)dx > $$ 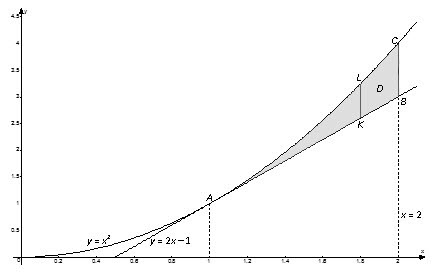Из рисунка в области $D$ видно, что левая граница контура области – одна линия < положительная ветка параболы $y= < < x >^ < 2 >> $), а его правая часть состоит из двух линий $AB$ < отрезок прямой $y=2x-1$) и $BC$ < отрезок прямой $x=2$), то есть задается разными уравнениями. В этом случае область $D$ нужно разбить на части так, чтобы каждая из них справа была ограничена только одной линией. В данном случае такими частями будут $ < < D >_ < 1 >> -ABF$ и $ < < D >_ < 2 >> -BCF$. Заданная область $D$ будет суммой областей $ < < D >_ < 1 >> $ и $ < < D >_ < 2 >> $. Тогда искомый интеграл будет равен сумме интегралов по каждой из областей:

$$\iint\limits_ < D > < \left( < < x >^ < 2 >> +2y \right)dxdy > =\iint\limits_ < < < D >_ < 1 >> > < \left( < < x >^ < 2 >> +2y \right)dxdy > +\iint\limits_ < < < D >_ < 2 >> > < \left( < < x >^ < 2 >> +2y \right)dxdy > $$

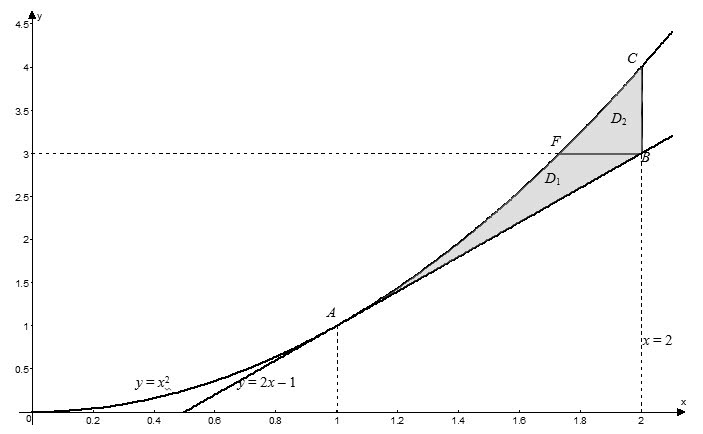
Поскольку в данном случае внутреннее интегрирование проводится по переменной $x$, то уравнения ограничивающих линий нужно разрешить относительно этой переменной:

$$AB:y=2x-1\Rightarrow x=\frac < y+1 > < 2 >; \qquad AC:y= < < x >^ < 2 >> \Rightarrow x=\sqrt < y >$$

Найдем пределы интегрирования для каждой из областей. В области $ < < D >_ < 1 >> $ переменная $y$ изменяется от ординаты точки $A$ до ординат точек $B$ и $F$. Точка $A$ принадлежит параболе $y= < < x >^ < 2 >> $ и выше было найдено, что абсцисса этой точки $ < < x >_ < A >> =1$, тогда $ < < y >_ < A >> = < < 1 >^ < 2 >> =1$. Точка $B$ – точка пересечения двух прямых $x=2$ и $y=2x-1$, а тогда $ < < y >_ < B >> =2\cdot 2-1=3$. Итак имеем, что $1\le y\le 3$. Переменная $x$ в области $ < < D >_ < 1 >> $ изменяется от ветки параболы $x=\sqrt < y >$ до прямой $x=\frac < y+1 > < 2 >$, то есть $ < < D >_ < 1 >> :\left[ \begin < matrix >1\le y\le 3, \\ \sqrt < y >\le x\le \frac < y+1 > < 2 >. \\ \end < matrix >\right.$ Аналогично для области $ < < D >_ < 2 >> $ находим, что $ < < D >_ < 2 >> :\left[ \begin < matrix >3\le y\le 4, \\ \sqrt < y >\le x\le 2. \\ \end < matrix >\right.$

Вычислить двойной интеграл (\iint\limits_R < \left( < < x^2 >+ < y^2 >>\right)dydx > ,) преобразовав его в полярные координаты. Область интегрирования (R) представляет собой сектор (0 \le \theta \le \large\frac < \pi > < 2 >\normalsize) круга радиусом (r = \sqrt 3.)

Вычислить интеграл (\iint\limits_R < xydydx >,) в котором область интегрирования (R) представляет собой кольцо, ограниченное окружностями ( < x^2 >+ < y^2 >= 1) и ( < x^2 >+ < y^2 >= 5.)

Решение:

В полярных координатах область интегрирования (R) является полярным прямоугольником: $R = \left( < \left( < r,\theta >\right)|\;1 \le r \le \sqrt 5 ,0 \le \theta \le 2\pi >\right).$

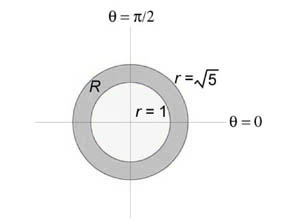
Найти интеграл (\iint\limits_R < \sin \theta drd\theta >,) где область интегрирования (R) ограничена кардиоидой (r = 1 + \cos \theta ).

Решение:

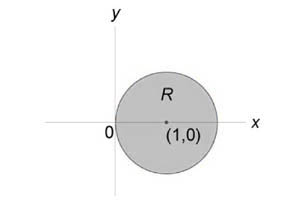
Вычислить интеграл (\iint\limits_R < \left( < < x^2 >+ < y^2 >>\right)dxdy > ) в круге ( < x^2 >+ < y^2 >= 2x.)

Решение: Область интегрирования (R) показана на рисунке:

Преобразуем уравнение окружности следующим образом: $ < < x^2 >+ < y^2 >= 2x, > \;\; < \Rightarrow < x^2 >— 2x + 1 + < y^2 >= 1, > \;\; < \Rightarrow < \left( < x - 1 >\right)^2 > + < y^2 >= 1. > $ Подставляя (x = r\cos \theta ,) (y = r\sin \theta ,) найдем уравнение окружности в полярных координатах. $ < < x^2 >+ < y^2 >= 2x, > \;\; < \Rightarrow < r^2 > < \cos ^2 >\theta + < r^2 > < \sin^2 >\theta = 2r\cos \theta , > \;\; < \Rightarrow < r^2 >\left( < < < \cos >^2 > \theta + < \sin^2 >\theta >\right) = 2r\cos \theta , > \;\; < \Rightarrow r = 2\cos \theta . >$ Образ (S) области интегрирования (R) показан на рисунке:

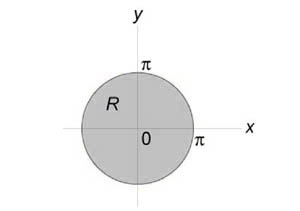
Вычислить двойной интеграл (\iint\limits_R < \sin \sqrt < < x^2 >+ < y^2 >> dxdy > ) посредством преобразования в полярные координаты. Область интегрирования (R) представляет собой круг ( < x^2 >+ < y^2 >\le < \pi ^2 >.)

Решение:

Область интегрирования (R) представлена на рисунке:

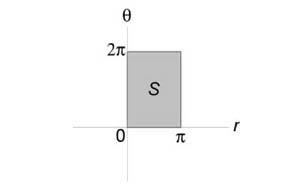
Образ (S) данной области описывается множеством (\left[< S = \left( < r,\theta >\right)|\;0 \le r \le \pi ,0 \le \theta \le 2\pi >\right]) и показан на рисунке:

Далее:

Свойства тройного интеграла

СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице

Теорема об аналоге СДНФ в Pk

Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному

Вычисление площади поверхности

Формула Гаусса — Остроградского

Булевы функции от $n$ переменных

Инвариантное определение дивергенции

СДНФ. Теорема о представлении в виде СДНФ. Построение СДНФ по таблице

Замена переменных в тройном интеграле

Дифференциальные характеристики векторного поля

Критерий полноты

Вычисление двойного интеграла

Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности

Теорема Остроградского

Огравление $\Rightarrow $

Источник