Рассчитайте энтропию состояния которое можно реализовать только одним способом ответ

Энтропия. Второй и третий законы термодинамики

Термодинамические системы характеризуются различной степенью неупорядоченности. Так, например, водяной пар менее упорядочен, чем лед; система, состоящая из воды и хлорида натрия в виде отдельных фаз, более упорядочена, чем раствор, приготовленный из этих веществ. Для количественной характеристики неупорядоченности системы в термодинамике используют специальную термодинамическую функцию — энтропию (S). Чем больше энтропия системы, тем больше её неупорядоченность.

При переходе системы из одного состояния в другое энтропия может как повышаться, так и понижаться. Примерами процессов, протекающих с повышением энтропии, могут служить плавление, кипение, диффузия, растворение кристаллических веществ в жидкостях. Процессы, обратные рассмотренным, сопровождаются понижением энтропии. Для химических реакций энтропия увеличивается, если процесс сопровождается увеличением числа молекул газообразных соединений. В случае реакций, в которых участвуют только кристаллические вещества, энтропия меняется незначительно. Рассмотрим, как можно количественно охарактеризовать энтропию системы.

Состояние термодинамической системы можно задать двояко:

1) Указать значения макропараметров системы — давления, объема, температуры, количества вещества. Состояние системы, заданное таким способом, называется макросостоянием.

2) Указать параметры всех частиц, образующих систему — координаты, импульсы и энергии; состояние системы, заданное микропараметрами частиц, называется микросостоянием. Очевидно, что каждому макросостоянию отвечает несколько (зачастую огромное число) микросостояний.

Число микросостояний, позволяющих реализовать то или иное макросостояние, называется его термодинамической вероятностью (W). Чем выше термодинамическая вероятность, тем чаще система будет находиться в этом состоянии.

Рассмотрим в качестве модельной системы распределение четырех молекул газа по двум половинам сосуда, разделенным условной перегородкой.

W = 1 W = 4 W = 6 W = 4 W = 1

Первое состояние можно реализовать только одним способом. Второе состояние можно реализовать четырьмя способами, меняя молекулу в левой части системы. При реализации третьего состояния возможны шесть перестановок молекул, поэтому вероятность данного состояния равна шести. Очевидно, что термодинамическая вероятность, а соответственно и энтропия состояния, отвечающего равномерному распределению молекул в системе максимальна.

Энтропия моля вещества связана с термодинамической вероятностью уравнением Больцмана

где R — универсальная газовая постоянная. Значение энтропии, равное 1 Дж/моль×К, называется энтропийной единицей (э.е.). Для одной частицы уравнение Больцмана имеет вид:

где k — постоянная Больцмана

=1,38 . 10 -23 Дж/К, где N_A — число Авогадро.

Как указывалось выше, состояние системы реализуется тем чаще, чем больше термодинамическая вероятность этого состояния. Отсюда можно заключить, что чем больше энтропия, тем больше вероятность перехода системы в состояние, отвечающее этой энтропии. Это заключение выражает суть второго закона термодинамики: изолированная система самопроизвольно изменяется в направлении состояния, обладающего максимальной энтропией.

Часто используют другую формулировку второго закона термодинамики: Теплота не может самопроизвольно переходить от холодного тела к горячему. Эти две формулировки взаимосвязаны и равноценны. Действительно, переход теплоты от холодного тела к горячему сопровождается сосредоточиванием в одной части системы быстрых («горячих») молекул, а в другой — медленных («холодных»). Упорядоченность системы при этом возрастает, а термодинамическая вероятность и энтропия понижаются. Согласно первой формулировке второго закона термодинамики такой процесс не может протекать самопроизвольно, если система не обменивается с другими системами энергией. Таким образом, процессы, идущие с понижением энтропии, в изолированной системе являются вынужденными.

Изменение энтропии системы при переходе из начального состояния в конечное:

,

где W₁ и W₂ — термодинамические вероятности начального и конечного состояния системы.

На энтропию оказывают влияние следующие факторы:

1. Агрегатное состояние вещества. Фазовые переходы из кристаллического в жидкое, а затем в газообразное состояние сопровождаются повышением энтропии.

2. Сложность структуры частиц. Усложнение структуры влечет за собой увеличение энтропии. Так, например, для атомарного кислорода О, молекулярного кислорода О₂ и озона О₃ значения энтропии при стандартных условиях составляют 161, 205 и 239 Дж/моль×К. Это явление можно объяснить тем, что по мере усложнения структуры молекул для последних становятся возможными новые формы движения частиц, что сопровождается увеличением термодинамической вероятности состояния. Действительно, для атомарного кислорода частицы могут отличаться лишь поступательным движением, тогда как для молекулярного кислорода и озона возможно также вращательное и колебательное движение. При этом для угловых молекул озона набор разрешенных колебательных и вращательных движений больше, чем для линейной молекулы кислорода.

3. Температура. Повышение температуры приводит к возрастанию энтропии в связи с увеличением средней скорости движения молекул вещества. Если в температурном интервале от Т₁ до Т₂ не наблюдается фазовых переходов, изменение энтропии системы подчиняется уравнению

,

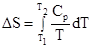
где С_р — молярная теплоемкость вещества. Для случая, когда С_р — величина постоянная,

Как следует из полученного уравнения, с повышением температуры энтропия увеличивается.

Если температура системы постоянна, а процесс является равновесным, изменение энтропии связано с тепловым эффектом процесса (ΔН) следующим уравнением:

Например, для фазовых переходов, являющихся равновесными изотермическими процессами:

,

где ΔН_ф.п. и Т_ф.п. тепловой эффект и температура фазового перехода. Если процесс не является равновесным, то

>

4. Давление. С увеличением давления энтропия понижается, но незначительно, особенно в конденсированных (твердых и жидких) системах. При повышении давления средние расстояния между частицами уменьшаются, взаимодействие между ними усиливается, и система становится более упорядоченной.

В отличие от всех остальных термодинамических функций для энтропии могут быть определены абсолютные ее значения, а не только изменение при переходе из одного состояния в другое. Пусть вещество находится при температуре абсолютного нуля. В такой системе движение частиц прекращается, и каждая из них имеет определенные, не изменяющиеся координаты. Подобному макросостоянию отвечает одно единственное микросостояние, а термодинамическая вероятность состояния равна единице, откуда

Рассмотренное явление позволяет сформулировать третий закон термодинамики: при температуре абсолютного нуля энтропия идеального кристалла равна нулю.

Для реальных кристаллов энтропия при температуре 0 К может несколько отличаться от нуля. Это явление можно объяснить наличием в таких кристаллах дефектов кристаллической решетки. Включения (атомы, оказавшиеся в междоузлиях кристаллической решетки) и вакансии (незанятые места в кристаллической решетке) повышают неупорядоченность структуры и, следовательно, энтропию системы.

В химической практике широко используют значения энтропии простых и сложных веществ, отнесенные к стандартным условиям. Эти величины называются стандартными энтропиями ( ); они приводятся в справочниках термодинамических свойств и используются при разнообразных термодинамических расчетах.

Поскольку энтропия является функцией состояния, изменение энтропии при протекании химической реакции

может быть вычислено по уравнению:

ΔS = [d (D) + e (E)] — [a (A) + b (B)];

или в общем виде

ΔS = Σi (пр) — Σj (реаг),

где i и j – коэффиенты в уравнении реакции.

Пример. Рассчитаем изменение энтропии, отвечающее синтезу карбоната кальция и силиката кальция из оксидов:

ΔS o = (СаСО₃) — [ (CаО) + (СО₂)] = 91,7 — (38,1 + 213,7) = -160,1 (Дж/моль×К)

ΔS o = (CaSiO₃) — [ (CaO) + (SiO₂)] = 81,0 — (38,1 + 4,2) = 1,7 (Дж/моль×К)

Как и следовало ожидать, реакция образования карбоната кальция, при которой происходит связывание газообразного вещества (СО₂), сопровождается существенным уменьшением энтропии системы, а при синтезе силиката кальция из кристаллических оксидов энтропия почти не изменяется.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.

Источник

Задачи к разделу Основы термодинамики с решениями

Здесь вы найдете примеры задач на вычисление таких термодинамических параметров как энтальпия, энтропия, энергия Гиббса. Определение возможности самопроизвольного протекания процесса, а также составление термохимических уравнений.

Задачи к разделу Основы термодинамики с решениями

Задача 1. Рассчитайте стандартную энтальпию и стандартную энтропию химической реакции. Определите в каком направлении при 298 °К (прямом или обратном) будет протекать реакция. Рассчитайте температуру, при которой равновероятны оба направления реакции.
Fe₂O_{3 (к)} + 3H₂ = 2Fe_(к) + 3H₂O_(г)

Используя справочные данные стандартных энтальпий веществ, находим:

Используя справочные данные стандартных энтропий веществ, находим:

При Т=298°К, ΔG > 0 – реакция не идет самопроизвольно, т.е. реакция будет протекать в обратном направлении.

Чтобы рассчитать температуру, при которой равновероятны оба направления реакции, надо ΔG приравнять к нулю:

При Т = 705,83 К реакция будет идти равновероятно как в прямом так и в обратном направлении.

Задача 2. Вычислите энергию Гиббса и определите возможность протекания реакции при температурах 1000 и 3000 К.

Cr2O3 (т) + 3C (т) = 2Cr (т) + 3CO (г)
ΔH298, кДж/моль	— 1141	0	0	— 110,6
ΔS298, Дж/(моль×К)	81,2	5,7	23,6	197,7

Вычисления энергии Гиббса проводим согласно выражению:

Необходимо рассчитать энтальпию и энтропию химической реакции.

Используя справочные данные стандартных энтальпий веществ, находим:

Аналогично, используя справочные данные стандартных энтропий веществ, находим:

Найдем энергию Гиббса при 1000 К

ΔG₁₀₀₀ > 0, следовательно, реакция самопроизвольно не идет.

Найдем энергию Гиббса при 3000 К

ΔG3₀₀₀ ˂ 0, следовательно, реакция протекает самопроизвольно.

Задача 3. Определите тепловой эффект сгорания жидкого CS₂(ж) до образования газообразных СО₂ и SO_2. Сколько молей CS₂ вступят в реакцию, если выделится 700 кДж тепла?

Уравнение реакции сгорания жидкого сероуглерода следующее:

Тепловой эффект реакции вычислим подставляя справочные данные стандартных энтальпий веществ в выражение:

Т.е. при сгорании 1 моля сероуглерода выделяется 1075,1 кДж тепла

а при сгорании x молей сероуглерода выделяется 700 кДж тепла

Найдем х:

x = 700·1/1075,1 = 0,65 моль

Итак, если в результате реакции выделится 700 кДж тепла, то в реакцию вступят 0,65 моль CS₂

Задача 4. Вычислите тепловой эффект реакции восстановления оксида железа (II) водородом, исходя из следующих термохимических уравнений:
1. FeO (к) + CO (г) = Fe (к) + CО₂ (г); ΔH₁ = -18,20 кДж;
2. СO (г) + 1/2O₂ (г) = СO₂ (г) ΔН₂ = -283,0 кДж;
3. H₂ (г) + ½ O₂ (г) = H₂O (г) ΔН₃ = -241,83 кДж.

Реакция восстановления оксида железа (II) водородом имеет следующий вид:

4. FeO (к) + H₂ (г) = Fe (к) + H₂O (г)

Чтобы вычислить тепловой эффект реакции необходимо применить закон Гесса, т.е. реакцию 4. можно получить, если сложить реакции 1. и 2. и вычесть реакцию 1.:

Таким образом, тепловой эффект реакции восстановления оксида железа (II) водородом равен

Задача 5. Реакция горения бензола выражается термохимическим уравнением:
С₆Н_6(ж) + 7½ О_2(г) = 6СО_2(г) + 3Н₂О_(г) – 3135,6 кДж.
Вычислите теплоту образования жидкого бензола. Определите теплотворную способность жидкого бензола при условии, что стандартные условия совпадают с нормальными.

Тепловой эффект реакции равен:

В нашем случае ΔH_р-ции = – 3135,6 кДж, найдем теплоту образования жидкого бензола:

Теплотворная способность жидкого бензола вычисляется по формуле:

М(бензола) = 78 г/моль

Q_Т = – 3135,6· 1000 / 78 = — 4,02·10 4 кДж/кг

Теплотворная способность жидкого бензола Q_Т = — 4,02·10 4 кДж/кг

Задача 6. Реакция окисления этилового спирта выражается уравнением:
С₂Н₅ОН_(ж) + 3,0 О_2(г) = 2СО_2(г) + 3Н₂О_(ж).
Определить теплоту образования С₂Н₅ОН_(ж), зная ΔН х.р. = — 1366,87 кДж. Напишите термохимическое уравнение. Определите мольную теплоту парообразования С₂Н₅ОН_(ж) → С₂Н₅ОН_(г), если известна теплота образования С₂Н₅ОН_(г), равная –235,31 кДж·моль -1 .

Исходя из приведенных данных, запишем термохимическое уравнение:

Тепловой эффект реакции равен:

Используя справочные данные теплот образования веществ, найдем теплоту образования С₂Н₅ОН_(ж):

ΔH 0 _C2H5OH(ж) = -277,36 кДж/моль

ΔH 0 _{парообразования} = — 235,31 + 277,36 = 42,36 кДж/моль

Мы определили, что теплота образования С₂Н₅ОН_(ж) равна

ΔH 0 _C2H5OH(ж) = -277,36 кДж/моль

ΔH 0 _{парообразования} = 42,36 кДж/моль

Задача 7. Чем можно объяснить, что при стандартных условиях, невозможна экзотермическая реакция:
СО_{2 (г)}+Н_{2 (г)} ↔ СО _(г)+Н₂О _(ж)?
Рассчитайте ΔG данной реакции. При каких температурах данная реакция становится самопроизвольной?

Рассчитаем ΔG данной реакции:

Для этого сначала определим ΔH и ΔS реакции:

Используя справочные данные стандартных энтальпий веществ, находим:

Аналогично, используя справочные данные стандартных энтропий веществ, находим:

Найдем энергию Гиббса при стандартных условиях

следовательно, реакция самопроизвольно не идет.

Найдем при каких температурах данная реакция становится самопроизвольной.

В состоянии равновесия ΔG_р-ции= 0, тогда

Задача 8. Рассчитав на основании табличных данных ΔG и ΔS, определите тепловой эффект реакции:
2 NO _(г) + Cl_{2 (г)} ↔ 2 NOCl_(г).

При постоянных температуре и давлении, изменение энергии Гиббса связано с энтальпией и энтропией выражением:

На основании табличных данных рассчитаем ΔG и ΔS

ΔH = — 40,64 + 298 · (-121,04/1000) = — 76,7 кДж/моль

Тепловой эффект реакции ΔH = — 76,7 кДж/моль

Задача 9. С чем будет более интенсивно взаимодействовать газообразный хлористый водород (в расчете на 1 моль): с алюминием или с оловом? Ответ дайте, рассчитав ΔG 0 обеих реакций. Продуктами реакций являются твердая соль и газообразный водород.

Рассчитаем ΔG 0 для реакции взаимодействия газообразного хлористого водорода (в расчете на 1 моль) с алюминием

В реакции принимает участие 2 моль Al(т), тогда ΔG_р-ции1 1 моля Al(т) равно

ΔG 0 _{р-ции 1} = -701,98 / 2 = -350,99 кДж/моль

Рассчитаем ΔG 0 для реакции взаимодействия газообразного хлористого водорода (в расчете на 1 моль) с оловом:

ΔG 0 _{р-ции 2} = -288,4 + 0- 0- 2·(-95,27) = -97,86 кДж/моль

Задача 10. Не прибегая к вычислениям, определите, какие знаки (>0, 0.

Источник