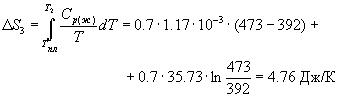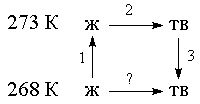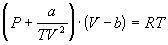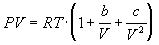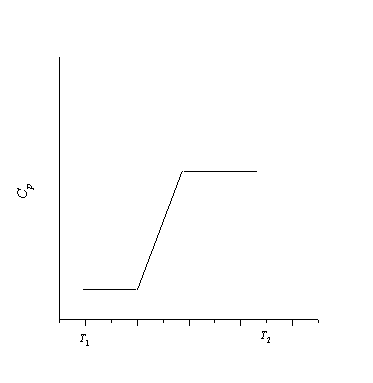Энтропия. Второй и третий законы термодинамики
Термодинамические системы характеризуются различной степенью неупорядоченности. Так, например, водяной пар менее упорядочен, чем лед; система, состоящая из воды и хлорида натрия в виде отдельных фаз, более упорядочена, чем раствор, приготовленный из этих веществ. Для количественной характеристики неупорядоченности системы в термодинамике используют специальную термодинамическую функцию — энтропию (S). Чем больше энтропия системы, тем больше её неупорядоченность.
При переходе системы из одного состояния в другое энтропия может как повышаться, так и понижаться. Примерами процессов, протекающих с повышением энтропии, могут служить плавление, кипение, диффузия, растворение кристаллических веществ в жидкостях. Процессы, обратные рассмотренным, сопровождаются понижением энтропии. Для химических реакций энтропия увеличивается, если процесс сопровождается увеличением числа молекул газообразных соединений. В случае реакций, в которых участвуют только кристаллические вещества, энтропия меняется незначительно. Рассмотрим, как можно количественно охарактеризовать энтропию системы.
Состояние термодинамической системы можно задать двояко:
1) Указать значения макропараметров системы — давления, объема, температуры, количества вещества. Состояние системы, заданное таким способом, называется макросостоянием.
2) Указать параметры всех частиц, образующих систему — координаты, импульсы и энергии; состояние системы, заданное микропараметрами частиц, называется микросостоянием. Очевидно, что каждому макросостоянию отвечает несколько (зачастую огромное число) микросостояний.
Число микросостояний, позволяющих реализовать то или иное макросостояние, называется его термодинамической вероятностью (W). Чем выше термодинамическая вероятность, тем чаще система будет находиться в этом состоянии.
Рассмотрим в качестве модельной системы распределение четырех молекул газа по двум половинам сосуда, разделенным условной перегородкой.
W = 1 W = 4 W = 6 W = 4 W = 1
Первое состояние можно реализовать только одним способом. Второе состояние можно реализовать четырьмя способами, меняя молекулу в левой части системы. При реализации третьего состояния возможны шесть перестановок молекул, поэтому вероятность данного состояния равна шести. Очевидно, что термодинамическая вероятность, а соответственно и энтропия состояния, отвечающего равномерному распределению молекул в системе максимальна.
Энтропия моля вещества связана с термодинамической вероятностью уравнением Больцмана
где R — универсальная газовая постоянная. Значение энтропии, равное 1 Дж/моль×К, называется энтропийной единицей (э.е.). Для одной частицы уравнение Больцмана имеет вид:
где k — постоянная Больцмана

Как указывалось выше, состояние системы реализуется тем чаще, чем больше термодинамическая вероятность этого состояния. Отсюда можно заключить, что чем больше энтропия, тем больше вероятность перехода системы в состояние, отвечающее этой энтропии. Это заключение выражает суть второго закона термодинамики: изолированная система самопроизвольно изменяется в направлении состояния, обладающего максимальной энтропией.
Часто используют другую формулировку второго закона термодинамики: Теплота не может самопроизвольно переходить от холодного тела к горячему. Эти две формулировки взаимосвязаны и равноценны. Действительно, переход теплоты от холодного тела к горячему сопровождается сосредоточиванием в одной части системы быстрых («горячих») молекул, а в другой — медленных («холодных»). Упорядоченность системы при этом возрастает, а термодинамическая вероятность и энтропия понижаются. Согласно первой формулировке второго закона термодинамики такой процесс не может протекать самопроизвольно, если система не обменивается с другими системами энергией. Таким образом, процессы, идущие с понижением энтропии, в изолированной системе являются вынужденными.
Изменение энтропии системы при переходе из начального состояния в конечное:

где W1 и W2 — термодинамические вероятности начального и конечного состояния системы.
На энтропию оказывают влияние следующие факторы:
1. Агрегатное состояние вещества. Фазовые переходы из кристаллического в жидкое, а затем в газообразное состояние сопровождаются повышением энтропии.
2. Сложность структуры частиц. Усложнение структуры влечет за собой увеличение энтропии. Так, например, для атомарного кислорода О, молекулярного кислорода О2 и озона О3 значения энтропии при стандартных условиях составляют 161, 205 и 239 Дж/моль×К. Это явление можно объяснить тем, что по мере усложнения структуры молекул для последних становятся возможными новые формы движения частиц, что сопровождается увеличением термодинамической вероятности состояния. Действительно, для атомарного кислорода частицы могут отличаться лишь поступательным движением, тогда как для молекулярного кислорода и озона возможно также вращательное и колебательное движение. При этом для угловых молекул озона набор разрешенных колебательных и вращательных движений больше, чем для линейной молекулы кислорода.
3. Температура. Повышение температуры приводит к возрастанию энтропии в связи с увеличением средней скорости движения молекул вещества. Если в температурном интервале от Т1 до Т2 не наблюдается фазовых переходов, изменение энтропии системы подчиняется уравнению
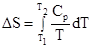
где Ср — молярная теплоемкость вещества. Для случая, когда Ср — величина постоянная,
Как следует из полученного уравнения, с повышением температуры энтропия увеличивается.
Если температура системы постоянна, а процесс является равновесным, изменение энтропии связано с тепловым эффектом процесса (ΔН) следующим уравнением:
Например, для фазовых переходов, являющихся равновесными изотермическими процессами:

где ΔНф.п. и Тф.п. тепловой эффект и температура фазового перехода. Если процесс не является равновесным, то

4. Давление. С увеличением давления энтропия понижается, но незначительно, особенно в конденсированных (твердых и жидких) системах. При повышении давления средние расстояния между частицами уменьшаются, взаимодействие между ними усиливается, и система становится более упорядоченной.
В отличие от всех остальных термодинамических функций для энтропии могут быть определены абсолютные ее значения, а не только изменение при переходе из одного состояния в другое. Пусть вещество находится при температуре абсолютного нуля. В такой системе движение частиц прекращается, и каждая из них имеет определенные, не изменяющиеся координаты. Подобному макросостоянию отвечает одно единственное микросостояние, а термодинамическая вероятность состояния равна единице, откуда
Рассмотренное явление позволяет сформулировать третий закон термодинамики: при температуре абсолютного нуля энтропия идеального кристалла равна нулю.
Для реальных кристаллов энтропия при температуре 0 К может несколько отличаться от нуля. Это явление можно объяснить наличием в таких кристаллах дефектов кристаллической решетки. Включения (атомы, оказавшиеся в междоузлиях кристаллической решетки) и вакансии (незанятые места в кристаллической решетке) повышают неупорядоченность структуры и, следовательно, энтропию системы.
В химической практике широко используют значения энтропии простых и сложных веществ, отнесенные к стандартным условиям. Эти величины называются стандартными энтропиями ( 
Поскольку энтропия является функцией состояния, изменение энтропии при протекании химической реакции
может быть вычислено по уравнению:
ΔS = [d 



или в общем виде
ΔS = Σi 

где i и j – коэффиенты в уравнении реакции.
Пример. Рассчитаем изменение энтропии, отвечающее синтезу карбоната кальция и силиката кальция из оксидов:
ΔS o = 


ΔS o = 


Как и следовало ожидать, реакция образования карбоната кальция, при которой происходит связывание газообразного вещества (СО2), сопровождается существенным уменьшением энтропии системы, а при синтезе силиката кальция из кристаллических оксидов энтропия почти не изменяется.
Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой.
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰).
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.
Источник
Рассчитайте энтропию состояния которое можно реализовать только одним способом формула
Второй закон термодинамики устанавливает критерии необратимости термодинамических процессов. Известно много формулировок второго закона, которые эквивалентны друг другу. Мы приведем здесь только одну формулировку, связанную с энтропией.
Существует функция состояния — энтропия S, которая обладает следующим свойством:
, (4.1) где знак равенства относится к обратимым процессам, а знак больше — к необратимым.
Для изолированных систем второй закон утверждает: dS і 0, (4.2) т.е. энтропия изолированных систем в необратимых процессах может только возрастать, а в состоянии термодинамического равновесия она достигает максимума (dS = 0,
d 2 S -23 Дж/К — постоянная Больцмана (k = R / NA), W — так называемая термодинамическая вероятность, т.е. число микросостояний, которые соответствуют данному макросостоянию системы (см. гл. 10). Формулу (4.4) называют формулой Больцмана.
С точки зрения строгой статистической термодинамики энтропию вводят следующим образом:
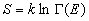
где G (E) — фазовый объем, занятый микроканоническим ансамблем с энергией E.
Термодинамическое определение энтропии основано на рассмотрении обратимых процессов:
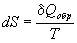
Это определение позволяет представить элементарную теплоту в такой же форме, как и различные виды работы:
Qобр = TdS, (4.7)
где температура играет роль обобщенной силы, а энтропия — обобщенной (тепловой) координаты.
Расчет изменения энтропии для различных процессов
Термодинамические расчеты изменения энтропии основаны на определении (4.6) и на свойствах частных производных энтропии по термодинамическим параметрам:
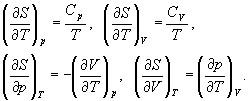
Последние два тождества представляют собой соотношения Максвелла (вывод см. в гл. 5).
1) Нагревание или охлаждение при постоянном давлении.
Количество теплоты, необходимое для изменения температуры системы, выражают с помощью теплоемкости: Qобр = Cp dT.
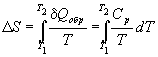
Если теплоемкость не зависит от температуры в интервале от T1 до T2, то уравнение (4.8) можно проинтегрировать:
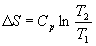
Если изменение температуры происходит при постоянном объеме, то в формулах (4.9) и (4.10) Cp надо заменить на CV.
2) Изотермическое расширение или сжатие.
Для расчета энтропии в этом случае надо знать уравнение состояния системы. Расчет основан на использовании соотношения Максвелла:
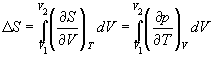
В частности, для изотермического расширения идеального газа (p = nRT / V)
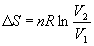
Этот же результат можно получить, если использовать выражение для теплоты изотермического обратимого расширения идеального газа: Qобр = nRT ln(V2/V1).
3) Фазовые переходы.
При обратимом фазовом переходе температура остается постоянной, а теплота фазового перехода при постоянном давлении равна Hфп, поэтому изменение энтропии равно:
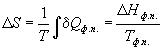
При плавлении и кипении теплота поглощается, поэтому энтропия в этих процессах возрастает: Sтв о С при давлении 1 атм. Мольная теплоемкость серы равна:
Температура плавления моноклинной серы 119 о С, удельная теплота плавления 45.2 Дж/г.
Решение. Общее изменение энтропии складывается из трех составляющих: 1) нагревание твердой серы от 25 до 119 о С, 2) плавление, 3) нагревание жидкой серы от 119 до 200 о С.
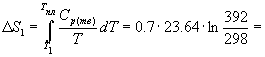
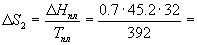
S = S1 + S2 + S3 = 11.88 Дж/К.
Пример 4-3. Найдите изменение энтропии газа и окружающей среды, если n молей идеального газа расширяются изотермически от объема V1 до объема V2: а) обратимо; б) против внешнего давления p.
Решение. а) Изменение энтропии газа при обратимом изотермическом расширении можно найти с помощью термодинамического определения энтропии с расчетом теплоты расширения по первому закону:
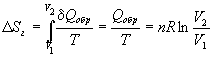
Так как расширение обратимое, то общее изменение энтропии Вселенной равно 0, поэтому изменение энтропии окружающей среды равно изменению энтропии газа с обратным знаком:
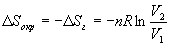
б) Энтропия — функция состояния, поэтому изменение энтропии системы не зависит от того, как совершался процесс — обратимо или необратимо. Изменение энтропии газа при необратимом расширении против внешнего давления будет таким же, как и при обратимом расширении. Другое дело — энтропия окружающей среды, которую можно найти, рассчитав с помощью первого закона теплоту, переданную системе:
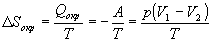
В этом выводе мы использовали тот факт, что U = 0 (температура постоянна). Работа, совершаемая системой против постоянного внешнего давления равна: A = p(V2—V1), а теплота, принятая окружающей средой, равна работе, совершенной системой, с обратным знаком.
Общее изменение энтропии газа и окружающей среды больше 0:
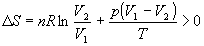
как и полагается для необратимого процесса.
Пример 4-4. Рассчитайте изменение энтропии 1000 г воды в результате ее замерзания при -5 О С. Теплота плавления льда при 0 о С равна 6008 Дж/моль. Теплоемкости льда и воды равны 34.7 и 75.3 Дж/(моль . К), соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс — самопроизвольный.
Решение. Необратимый процесс замерзания воды при температуре -5 О С можно представить в виде последовательности обратимых процессов: 1) нагревание воды от
-5 О С до температуры замерзания (0 О С); 2) замерзание воды при 0 О С; 3) охлаждение льда от 0 до -5 О С:
Изменение энтропии в первом и третьем процессах (при изменении температуры) рассчитывается по формуле (4.9):
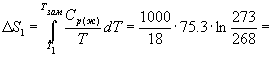
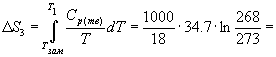
Изменение энтропии во втором процессе рассчитывается как для обычного фазового перехода (4.13). Необходимо только иметь в виду, что теплота при замерзании выделяется:
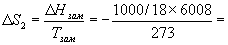
Т.к. энтропия — функция состояния, общее изменение энтропии равно сумме по этим трем процессам:
S = S1 + S2 + S3 = -1181 Дж/К.
Энтропия при замерзании убывает, хотя процесс самопроизвольный. Это связано с тем, что в окружающую среду выделяется теплота и энтропия окружающей среды увеличивается, причем это увеличение больше, чем 1181 Дж/К, поэтому энтропия Вселенной при замерзании воды возрастает, как и полагается в необратимом процессе.
ЗАДАЧИ
4-1. Приведите пример термодинамического процесса, который может быть проведен как обратимо, так и необратимо. Рассчитайте изменение энтропии системы и окружающей среды в обоих случаях.
4-2. Проверьте неравенство Клаузиуса для циклического процесса, представленного в задаче 2.14.
4-3. Рассчитайте мольную энтропию неона при 500 К, если при 298 К и том же объеме энтропия неона равна 146.2 Дж/(моль . К).
4-4. Рассчитайте изменение энтропии при нагревании 11.2 л азота от 0 до 50 о С и одновременном уменьшении давления от 1 атм до 0.01 атм.
4-5. Один моль гелия при 100 о С и 1 атм смешивают с 0.5 моль неона при 0 о С и 1 атм. Определите изменение энтропии, если конечное давление равно 1 атм.
4-6. Рассчитайте изменение энтропии при образовании 1 м 3 воздуха из азота и кислорода (20 об.%) при температуре 25 о С и давлении 1 атм.
4-7. Три моля идеального одноатомного газа (CV = 3.0 кал/(моль . К)), находящегося при T1 = 350 K и P1 = 5.0 атм, обратимо и адиабатически расширяются до давления P2 = 1.0 атм. Рассчитайте конечные температуру и объем, а также совершенную работу и изменение внутренней энергии, энтальпии и энтропии в этом процессе.
4-8. Рассчитайте изменение энтропии при нагревании 0.4 моль хлорида натрия от 20 до 850 о С. Мольная теплоемкость хлорида натрия равна:
Температура плавления хлорида натрия 800 о С, теплота плавления 31.0 кДж/моль.
4-9. Рассчитайте изменение энтропии при смешении 5 кг воды при 80 о С с 10 кг воды при 20 о С. Удельную теплоемкость воды принять равной: Cp(H2O) = 4.184 Дж/(г . К).
4-10. Рассчитайте изменение энтропии при добавлении 200 г льда, находящегося при температуре 0 о С, к 200 г воды (90 о С) в изолированном сосуде. Теплота плавления льда равна 6.0 кДж/моль.
4-11. Для некоторого твердого тела найдена зависимость коэффициента расширения от давления в интервале давлений от p1 до p2:
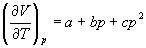
Насколько уменьшится энтропия этого тела при сжатии от p1 до p2?
4-12. Найдите изменение энтропии газа и окружающей среды, если n молей идеального газа расширяются изотермически от давления p1 до давления p2: а) обратимо; б) против внешнего давления p 0 С и давлении 2 атм.
4-14. Нарисуйте график зависимости стандартной энтропии воды от температуры в интервале от 0 до 400 К.
4-15. Запишите энтропию одного моля идеального газа как функцию температуры и давления (теплоемкость считать постоянной).
4-16. Определите зависимость энтропии от объема для термодинамической системы, которая описывается уравнением состояния (для одного моля):
4-17. Определите зависимость энтропии от объема для термодинамической системы, которая описывается уравнением состояния (для одного моля):
4-18. Один моль газа описывается уравнением состояния
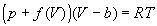
где f(V) — некоторая функция, которая не зависит от температуры. Рассчитайте изменение энтропии газа при его необратимом изотермическом расширении от объема V1 до объема V2.
4-19. Рассчитайте изменение энтропии 1000 г метанола в результате его замерзания при -105 О С. Теплота плавления твердого метанола при -98 о С (т.пл.) равна 3160 Дж/моль. Теплоемкости твердого и жидкого метанола равны 55.6 и 81.6 Дж/(моль . К), соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс — самопроизвольный.
4-20. Теплоемкость некоторого вещества в интервале температур от T1 до T2 изменяется следующим образом:
Постройте график зависимости энтропии вещества от температуры в этом интервале температур.
4-21. Пользуясь справочными данными, приведите пример самопроизвольной химической реакции, для которой стандартное изменение энтропии меньше 0.
4-22. Пользуясь справочными данными, рассчитайте стандартное изменение энтропии в реакции H2(г) + ЅO2(г) = H2O(г) а) при 25 о С; б) при 300 о С.


Сервер создается при поддержке Российского фонда фундаментальных исследований
Не разрешается копирование материалов и размещение на других Web-сайтах
Вебдизайн: Copyright (C) И. Миняйлова и В. Миняйлов
Copyright (C) Химический факультет МГУ
Написать письмо редактору
Источник




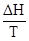




 , (4.1) где знак равенства относится к обратимым процессам, а знак больше — к необратимым.
, (4.1) где знак равенства относится к обратимым процессам, а знак больше — к необратимым.