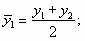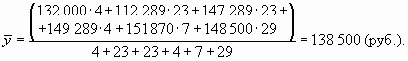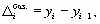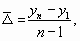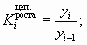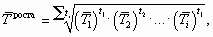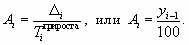Рассчитать базисным способом абсолютное изменение

Ряды динамики

Понятие рядов динамики (временных рядов)

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y₁ называют начальным или базисным уровнем, а последний y_n – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде таблицы или графика, причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

Пример ряда динамики

Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января

Год	2004	2005	2006	2007	2008	2009
Число жителей	144,2	143,5	142,8	142,2	142,0	141,9

График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января

Данные таблицы и графика наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.

Виды рядов динамики

Ряды динамики классифицируются по следующим основным признакам:

1. По времени — ряды моментные и интервальные (периодные), которые показывают уровень явления на конкретный момент времени или на определенный его период. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, общее количество проданных акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания, как правило, не имеет. Так, если сложить величины запасов на начало каждого месяца квартала, то полученная сумма не означает квартальную величину запасов.
2. По форме представления — ряды абсолютных, относительных и средних величин.
3. По интервалам времени — ряды равномерные и неравномерные (полные и неполные), первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается.
4. По числу смысловых статистических величин — ряды изолированные и комплексные (одномерные и многомерные). Первые представляют собой ряд динамики одной статистической величины (например, индекс инфляции), а вторые — нескольких (например, потребление основных продуктов питания).

В нашем примере про число жителей России ряд динамики: 1) моментный (приведены уровни на 1 января); 2) абсолютных величин (в млн.чел.); 3) равномерный (равные интервалы в 1 год); 4) изолированный.

Показатели изменения уровней ряда динамики

Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:

• абсолютное изменение (абсолютный прирост);
• относительное изменение (темп роста или индекс динамики);
• темп изменения (темп прироста).

Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.

Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше первого (базисного) уровня, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).

Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и может иметь знак «+» или «–».

В следующей расчетной таблице в столбце 3 рассчитаны базисные абсолютные изменения, а в столбце 4 – цепные абсолютные изменения.

Год	y					, %	,%
2004	144,2
2005	143,5	-0,7	-0,7	0,995	0,995	-0,49	-0,49
2006	142,8	-1,4	-0,7	0,990	0,995	-0,97	-0,49
2007	142,2	-2,0	-0,6	0,986	0,996	-1,39	-0,42
2008	142,0	-2,2	-0,2	0,985	0,999	-1,53	-0,14
2009	141,9	-2,3	-0,1	0,984	0,999	-1,60	-0,07
Итого	-2,3	0,984	-1,60

Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

.

В нашем примере про число жителей России подтверждается правильность расчета абсолютных изменений: = — 2,3 рассчитана в итоговой строке 4-го столбца, а = — 2,3 – в предпоследней строке 3-го столбца расчетной таблицы.

Базисное относительное изменение (базисный темп роста или базисный индекс динамики) представляет собой соотношение конкретного и первого уровней ряда, определяясь по формуле

Цепное относительное изменение (цепной темп роста или цепной индекс динамики) представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле

.

Относительное изменение показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i Следующая лекция.

• 
• 
• 

• Разработка интернет-магазина
• Редизайн сайта эвакуации
• Редизайн сайта доставки суши

Источник

Аналитические показатели динамики

Расчет аналитических производных показателей динамических рядов.

У нашего движка для создания калькуляторов онлайн появилась новая функциональность — возможность вводить для расчета произвольное число значений, иными словами, появилась входная таблица. Пользователь добавляет/редактирует/удаляет значения, калькулятор их подсчитывает.

Воспользовавшись этим, я немедленно создал калькулятор для расчета аналитических показателей статистических рядов динамики.
Тем более, что пользователь с ником Светлана очень давно просил калькулятор вычисляющий средний темп роста. Наконец-то это стало возможным. Но обо всем по порядку.

Начнем с теории.

Рядами динамики называются ряды расположенных в хронологическом порядке показателей, характеризующих изменение какой-либо величины во времени. Ряды динамики включают два основных элемента: показатели времени — t и соответствующие им показатели величины — Y.

Ряды динамики делятся на моментные и интервальные.
Моментные ряды динамики отображают состояние изучаемой величины на определенные момент времени. Интервальные ряды отображают состояние изучаемой величины за отдельные интервалы времени.

Приведу пример. Допустим, 1 января хлеб стоит 13 рублей, 1 февраля — 14 рублей, 1 марта — 15 рублей, это моментный ряд. Если за январь мы купили 10 буханок хлеба, за февраль — 12 буханок, за март — 14 буханок, это интервальный ряд. Заметим, что интервальный ряд обладает свойством суммарности, т. е. показатели можно складывать, и получится что-то осмысленное, например, потребление хлеба за три месяца.

Имея ряд показателей, можно просчитать всевозможные аналитические производные показатели. Производные показатели могут рассчитываться двумя основными способами — цепным и базисным.

При цепном методе каждый последующий показатель сопоставляется с предыдущим, при базисном — с одним и тем же показателем, принятым за базу сравнения. Обычно это первый показатель ряда.

Рассмотрим некоторые аналитические производные показатели:

Аналитические производные показатели

1. Абсолютный прирост
Разность значений двух показателей ряда динамики.

Базисный абсолютный прирост — разность текущего значения и значения принятого за постоянную базу сравнения

Цепной абсолютный прирост — разность текущего и предыдущего значений

2. Темп роста
Отношение двух уровней ряда (может выражаться в процентах).

Базисный темп роста — отношение текущего значения и значения принятого за постоянную базу сравнения

Цепной темп роста — отношение текущего и предыдущего значений

3. Темп прироста
Отношение абсолютного прироста к сравниваемому показателю.

Базисный темп прироста — отношение абсолютного базисного прироста и значения принятого за постоянную базу сравнения

Цепной темп прироста — отношение абсолютного цепного прироста и предыдущего значения показателя

4. Ускорение

Абсолютное ускорение — разница между абсолютным приростом за данный период и абсолютным приростом за предыдущий период равной длительности. Измеряется только цепным способом

Относительное ускорение — отношение цепного темпа прироста за данный период и цепного темпа прироста за предыдущий период

5. Темп наращивания
Отношение цепных абсолютных приростов к уровню, принятому за постоянную базу сравнения

6. Абсолютное значение одного процента прироста
Отношение абсолютного прироста к темпу прироста, выраженное в процентах.
После раскрытия формула упрощается до

Для получения обобщающих характеристик динамики изучаемого ряда рассчитываются средние показатели динамики.

Средние показатели динамики

1. Средний уровень
Характеризует типичную величину показателей

В интервальном динамическом ряду рассчитывается как простое арифметическое среднее

В моментном динамическом ряду с равными промежутками времени между отсчетами как хронологическое среднее

2. Средний абсолютный прирост
Обобщающий показатель скорости абсолютного изменения значений динамического ряда

3. Средний темп роста
Обобщающий характеристика темпов роста ряда динамики

(корень степени i — 1)

4. Средний темп прироста
Отношение тоже что и между темпом роста и темпом прироста

Все производные и средние показатели, приведенные здесь, рассчитываются в калькуляторе (см. ниже) по мере того, как пользователь вводит значения ряда в таблицу.

На своей личной странице зарегистрированные пользователи могут сохранить калькулятор и запомнить введенные в него значения для повторного использования.

Источник

Ряды динамики в статистике

9.2. Показатели ряда динамики

При анализе динамического ряда рассчитываются следующие показатели:

• средний уровень динамического ряда;
• абсолютные приросты: цепные и базисные, средний абсолютный прирост;
• темпы роста: цепные и базисные, средний темп роста;
• темпы прироста: цепные и базисные, средний темп прироста;
• абсолютное значение одного процента прироста.

Цепные и базисные показатели вычисляются для характеристики изменения уровней динамического ряда и различаются между собой базами сравнения: цепные рассчитываются по отношению к предыдущему уровню ( переменная база сравнения), базисные — к уровню, принятому за базу сравнения (постоянная база сравнения).

Средние показатели представляют собой обобщенные характеристики ряда динамики. С их помощью сравнивают интенсивность развития явления по отношению к различным объектам, например по странам, отраслям, предприятиям и т.д., или периодам времени.

9.2.1. Средний уровень ряда динамики

Конкретное числовое значение статистического показателя, относящееся к моменту или периоду времени, называется уровнем ряда динамики и обозначается через y_i (где i — показатель времени).

Методика расчета среднего уровня зависит от вида динамического ряда, а именно: является ли он моментным или интервальным, с равными или неравными временными промежутками между соседними датами.

Если дан интервальный ряд динамики абсолютных или средних величин с равными периодами времени, то для расчета среднего уровня применяется формула средней арифметической простой:

п — число уровней ряда.

Пример 9.2. По данным таблицы определим среднемесячный размер страхового возмещения, выплаченного страховой компанией, в расчете на один пострадавший объект за полугодие:

Таблица 9.6.

Месяц	Январь	Февраль	Март	Апрель	Май	Июнь
Средний размер выплаченного страхового возмещения, тыс. руб	106	108	108	111	110	112

Если временные промежутки интервального динамического ряда неравны, то значение среднего уровня находят по формуле средней арифметической взвешенной, в которой в качестве весов используют длину временных периодов, соответствующих уровням ряда динамики (t_i)

Пример 9.3. По данным, представленным в таблице, определим среднемесячный размер страхового возмещения, выплаченного страховой компанией, в расчете на один пострадавший объект:

Таблица 9.7.

Месяц	Январь	Февраль	Март	II квартал	III квартал	IV квартал
Средний размер выплаченного страхового возмещения, тыс. руб.	106	110	138	150	160	140

В моментных рядах динамики с одинаковыми временными промежутками между датами средний уровень ряда рассчитывается по формуле средней хронологической простой

где y_n — значения показателя на конец рассматриваемого периода.

Пример 9.4. По приведенным ниже данным о размере денежных средств на счете вкладчика на начало каждого месяца определим средний размер вклада в I квартале 2006 г.:

Таблица 9.8.

Дата	01.01.06	01.02.06	01.03.06	01.04.06
Остаток денежных средств, руб.	132 000	147 289	151 870	148 500

Средний уровень моментного ряда динамики равен:

Хотя I квартал включает три месяца (январь, февраль, март), в расчете должны быть использованы четыре уровня ряда (включая данные на 1 апреля). Это легко доказать. Действительно, если исчислять средние уровни по месяцам, то получим:

в январе

в феврале

в марте

Рассчитанные средние образуют интервальный ряд динамики с равными временными промежутками, в котором средний уровень исчисляется, как мы видели выше, по формуле средней арифметической простой:

Аналогично, если требуется рассчитать средний уровень моментного ряда динамики с равными интервалами между датами за первое полугодие, то в качестве последнего уровня в формуле средней хронологической простой следует взять данные на 1 июля, а если за год — данные на 1 января следующего года.

В моментных рядах динамики с неравными промежутками между датами для определения среднего уровня применяется формула средней хронологической взвешенной:

где t_i — длина временного периода между двумя соседними датами.

Пример 9.5. По данным о запасах товаров на начало месяца определим средний размер товарных запасов в 2006 г.

Таблица 9.9.

Дата	01.01.06	01.02.06	01.03.06	01.07.06	01.09.06	01.12.06	01.01.07
Запасы товаров, тыс. руб.	1 320	1 472	1 518	1 300	1 100	1 005	920

Средний уровень ряда равен:

Расстояние между датами

Если имеется полная информация о значениях моментного статистического показателя на каждую дату, то среднее значение этого показателя за весь период исчисляется по формуле средней арифметической взвешенной:

где y_i — значения показателя

t_i — длина периода, в течение которого это значение статистического показателя оставалось неизменным.

Если мы дополним пример 9.4 информацией о датах изменения денежных средств на счете вкладчика в I квартале 2006 г., то получим:

• остаток денежных средств на 1 января — 132 000 руб.;
• января выдано — 19 711 руб.;
• 28 января внесено — 35 000 руб.;
• 20 февраля внесено — 2000 руб.;
• 24 февраля внесено — 2581 руб.;
• 3 марта выдано — 3370 руб. (в марте других изменений не происходило).

Итак, с 1 по 4 января (четыре дня) значение показателя оставалось равным 132 000 руб., с 5 по 27 января (23 дня) его значение составило 112 289 руб., с 28 января по 19 февраля (23 дня) — 147 289 руб., с 20 по 23 февраля (четыре дня) — 149 289 руб., с 24 февраля по 2 марта (семь дней) — 151 870 руб., с 3 по 31 марта (29 дней) — 148 500 руб. Для удобства проведения расчетов представим эти данные в таблице:

Таблица 9.10.

Длина периода, дней	4	23	23	4	7	29
Остаток денежных средств, руб.	132 00	112 289	147 289	149 289	151 879	148 500

По формуле средней арифметической взвешенной находим значение среднего уровня ряда

Как видим, среднее значение отличается от полученного в примере 9.4, оно является более точным, так как в вычислениях использовалась более точная информация. В примере 9.4 были известны лишь данные на начало каждого месяца, при этом не оговаривалось, когда же именно происходили изменения показателя, была применена формула хронологической средней.

В заключение отметим, что расчет среднего уровня ряда теряет свой аналитический смысл в случаях большой изменяемости показателя внутри ряда, а также при резкой смене направления развития явления.

9.2.2. Показатели абсолютного изменения уровней динамического ряда

Абсолютные приросты рассчитываются как разность между двумя значениями соседних уровней динамического ряда (цепные приросты) или как разность между значениями текущего уровня и уровня, принятого за базу сравнения (базисные приросты). Показатели абсолютного прироста имеют те же единицы измерения, что и уровни динамического ряда. Они показывают, на сколько единиц изменился показатель при переходе от одного момента или периода времени к другому.

Базисные абсолютные приросты рассчитывают по формуле

где у_i — i-й текущий уровень ряда,

y₁ — первый уровень ряда динамики, принятый за базу сравнения.

Формула для определения цепных абсолютных приростов имеет вид

где у_i — 1 — уровень, предшествующий i-му уровню динамического ряда.

Средний абсолютный прирост показывает, на сколько единиц в среднем ежемесячно, или ежеквартально, или ежегодно и т.д. изменялось значение показателя в течение рассматриваемого периода времени. В зависимости от того, какими данными мы располагаем, его можно рассчитать следующими способами:

1. 

— цепные абсолютные приросты показателя;

где y_n — последний уровень ряда

Пример 9.6. По данным таблицы определим показатели абсолютных приростов размера страхового возмещения, выплаченного страховой компанией.

Таблица 9.11.

* Сумма всех рассчитанных цепных абсолютных приростов дает базисный абсолютный прирост последнего периода.

Среднемесячный абсолютный прирост за полугодие равен

Таким образом, в среднем ежемесячно размер выплат страхового возмещения увеличивался на 1,2 тыс. руб.

9.2.3. Показатели относительного изменения уровней динамического ряда

Характеристиками относительного изменения уровней ряда динамики являются коэффициенты и темпы роста значений показателя и темпы их прироста.

Коэффициент роста представляет собой соотношение двух уровней динамического ряда, выраженное в виде простого кратного отношения. Он показывает, во сколько раз изменилось значение показателя в одном периоде (моменте) времени по сравнению с другим. Темп роста — это коэффициент роста, выраженный в процентах. Он показывает, сколько процентов составляет значение показателя в данном периоде, если уровень, с которым проводится сравнение, принять за 100%.

Так же, как и абсолютные приросты, коэффициенты и темпы роста могут быть цепными и базисными.

Цепные коэффициент и темп роста измеряют относительное изменение текущего уровня показателя по сравнению с предшествующим ему уровнем:

Базисные коэффициент и темп роста характеризуют относительное изменение текущего уровня показателя по сравнению с базисным (чаще всего с первым) уровнем:

Цепные и базисные коэффициенты роста имеют между собой следующую связь:

• произведение всех рассчитанных до текущего периода цепных коэффициентов роста дает базисный коэффициент роста текущего периода:

Средние темп роста и коэффициент роста в динамических рядах с равноотстоящими уровнями рассчитываются по формуле средней геометрической простой

— цепные коэффициенты роста;

— цепные темпы роста.

Эти формулы могут быть приведены к следующему виду:

Для того чтобы определить, на сколько процентов текущий уровень показателя больше или меньше значения предшествующего или базисного уровня, рассчитываются темпы прироста. Они исчисляют путем вычитания 100% из соответствующих темпов роста:

• цепные темпы прироста:
• базисные темпы прироста:

Средний темп прироста рассчитывается аналогичным образом: из среднего темпа роста вычитаются 100%:

Пример 9.7. В таблице приведены рассчитанные коэффициенты роста, темпы роста и прироста показателя, характеризующего среднемесячный размер выплаченного компанией страхового возмещения за период с января по июнь.

Таблица 9.12.

Месяц	Средний размер выплаченного страхового возмещения, тыс. руб., yi	Коэффициент роста		Темпы роста, %		Темпы прироста, %		Абсолютное значение 1% прироста, тыс. руб.
		цепные	базисные	цепные	базисные	цепные	базисные
Январь	106	—	1	—	100	—	—	—
Февраль	108	1,019	1,019	101,9	101,9	1,9	1,9	1,06
Март	108	1,000	1,000	100,0	101,9	0	1,9	1,08
Апрель	111	1,028	1,047	102,8	104,7	2,8	4,7	1,08
Май	110	0,991	1,038	99,1	103,8	-0,9	3,8	1,11
Июнь	112	1,018	1,057	101,8	105,7	1,8	5,7	1,10

По формуле средней геометрической простой определим среднемесячный коэффициент роста показателя за период с февраля по июнь:

Средний темп роста, соответственно, равен 101,1%. Следовательно, в среднем ежемесячно размер выплат страхового возмещения увеличивался в 1,011 раза, или на 1,1%.

Если известны средние темпы (или коэффициенты) роста за некоторые неравные отрезки времени, то средний темп роста за весь период исчисляется по формуле средней геометрической взвешенной:

где Т_i — средний темп роста за i-й период времени;

t_i — длина i-го периода.

Пример 9.8. Среднегодовые коэффициенты роста числа страховых компаний в одной из областей России составили за период 1991-1995 гг. — 1,18; 1995-2000 гг. — 1,24; 2000-2004 — 1,56. Определим среднегодовой коэффициент роста числа страховых компаний за весь период с 1991 по 2004 гг.

Таким образом, за период с 1991 по 2004 гг. среднегодовой темп роста числа страховых компаний в одной из областей России составил 131,1%, соответственно, среднегодовой темп прироста — 31,1%.

Для более полного анализа динамики расчет цепных показателей роста и прироста уровней динамического ряда часто сопровождаются указаниями абсолютных значений 1% прироста.

Абсолютное значение 1% прироста (А_i) определяется как отношение значения абсолютного прироста показателя к его темпу прироста в i-й момент времени:

В последней графе таблицы примера 9.7 рассчитаны цепные абсолютные значения 1% прироста.

Источник