Распределительный способ умножения примеры

Свойства умножения

Переместительное свойство умножения

От перестановки сомножителей местами произведение не меняется.

Следовательно, для любых чисел a и b верно равенство:

выражающее переместительное свойство умножения.

4 · 2 · 3 = 3 · 2 · 4 = 24.

Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.

Сочетательное свойство умножения

Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.

Следовательно, для любых чисел a, b и c верно равенство:

выражающее сочетательное свойство умножения.

3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30

3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.

Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:

25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.

В данном случае можно было вычислить всё последовательно:

25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,

но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.

Распределительное свойство умножения

Сначала рассмотрим распределительное свойство умножения относительно сложения:

Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Следовательно, для любых чисел a, b и m верно равенство:

выражающее распределительное свойство умножения.

Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.

Следовательно, для любых чисел a, b и m верно равенство:

Теперь рассмотрим распределительное свойство умножения относительно вычитания:

Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

Переход от умножения:

соответственно к сложению и вычитанию:

называется раскрытием скобок.

Переход от сложения и вычитания:

называется вынесением общего множителя за скобки.

Источник

Урок 16 Бесплатно Применение распределительного свойства умножения

В этом уроке мы узнаем, как умножать смешанное число на натуральное, и разберем, как использовать распределительное свойство умножения для рационализации вычислений с обыкновенными дробями и смешанными числами.

Распределительное свойство умножения

Это свойство говорит нам о том, что если необходимо умножить одно число, назовем его a, на сумму двух других чисел, обозначим их b и c, то ответом будет сумма двух произведений: произведения a и b и произведения a и c

Напомним, коммутативное свойство — это научный термин для обычного правила, которое гласит, что перемена мест слагаемых (или множителей) не влияет на результат.

Вторая строка говорит о том же самом, что и первая; просто показывает, что коммутативное свойство умножения работает и в этом случае.

Умножение смешанного числа на натуральное используя распределительной свойство

В уроке «Умножение дробей» мы уже касались этих моментов. Теперь рассмотрим их более подробно.

Самый простой способ умножения смешанного числа на натуральное заключается в том, чтобы перевести смешанное число в натуральную дробь, домножив целую часть на знаменатель и прибавив его к числителю, а далее домножить полученную неправильную дробь на натуральное число, перемножив числитель дроби и натуральное число.

Это и будет результатом.

Пример:

Этот пример нам показывает, что даже такая простая операция, как умножение на 2, приводит нас к множеству умножений, сложений и даже делению. Для больших чисел такой путь неудобен. Стоит только представить, что целая часть смешанного числа будет больше 100, и знаменатель также также весьма сложный, то мы получим операции, которые с трудом делаются в уме.

Здесь нас выручит распределительное свойство.

Если представить \(\mathbf<43\frac<1><3>>\) как сумму его целой и дробной частей, то есть

\(\mathbf<43\frac<1><3>=43+\frac<1><3>>\), то нам нужно будет в дальнейшем умножать только 43 и \(\mathbf<\frac<1><3>>\), что значительно проще.

Посмотрим, как это все будет выглядеть целиком:

Можно заметить, что несмотря на то, что мы удлинили запись выражения, сами вычисления стали проще.

Может возникнуть необходимость выделения целой части, про это забывать нельзя. Но даже в таком случае делимое будет значительно меньше, чем если бы мы выносили целую часть из произведения, полученного классическим способом.

Пример:

Пройти тест и получить оценку можно после входа или регистрации

Источник

Свойства умножения и деления

О чем эта статья:

Свойства умножения

Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.

Узнаем, какие бывают свойства умножения и как их применять.

Переместительное свойство умножения

От перестановки мест множителей произведение не меняется.

То есть, для любых чисел a и b верно равенство: a * b = b * a.

Это свойство можно применять к произведениям, в которых больше двух множителей.

• 6 * 5 = 5 * 6 = 30;
• 4 * 2 * 3 = 3 * 2 * 4 = 24.

Сочетательное свойство умножения

Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.

То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).

3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30

3 * 2 * 5 = (3 * 2) * 5 = 6 * 5 = 30.

Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.

Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.

Распределительное свойство умножения относительно сложения

Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.

То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.

Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.

В обратную сторону распределительное свойство умножения относительно сложения звучит так:

Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Распределительное свойство умножения относительно вычитания

Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.

То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.

В обратную сторону распределительное свойство умножения относительно вычитания звучит так:

Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Свойство нуля при умножении

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.

Свойство единицы при умножении

Если умножить любое целое число на единицу, то в результате получится это же число.

То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.

Свойства деления

Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.

Основные свойства деления целых чисел

1. Деление на нуль невозможно.
2. Деление нуля на число: 0 : a = 0.
3. Деление равных чисел: a : a = 1.
4. Деление на единицу: a : 1 = a.
5. Для деления переместительное свойства не выполняется: a : b ≠ b : a.
6. Деление суммы и разности на число: (a ± b) : c = (a : c) ± (b : c).
7. Деление произведения на число:
   (a * b) : c = (a : c) * b, если a делится на c;
   (a * b) : c = a * (b : с), если b делится на c;
   (a * b) : c = a * (b : с) = (a : c) * b, если a и b делятся на c.
8. Деление числа на произведение:
   a : (b * c) = (a : b) * (1 : c) = (a : c) * (1 : b).

И еще одно важное свойство деления, которое проходят в 5 классе:

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.

Применим свойства деления на практике.

Пример 1

Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?

Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.

Пример 2

Вычислить: 500 * (100 : 5).

Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.

Ответ: 500 * (100 : 5) = 10000.

Пример 3

Упростить выражение: 27a – 16a.

Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 — 16) = a * 11 = 11a.

Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.

Источник

Умножение натуральных чисел: свойства, примеры

Для операции умножения натуральных чисел ℕ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.

Переместительное свойство умножения натуральных чисел

Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:

Переместительный закон умножения

От перемены мест множителей произведение не меняется.

В буквенном виде переместительное свойство записывается так: a · b = b · a

a и b — любые натуральные числа.

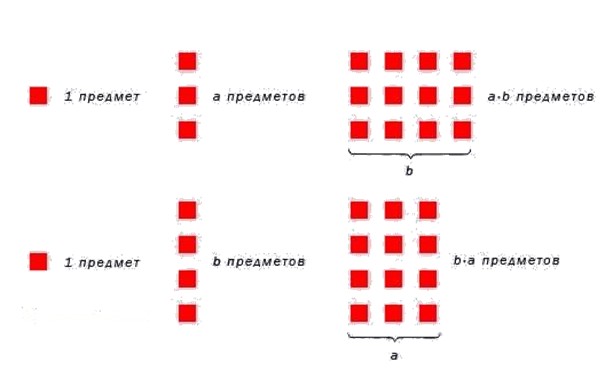
Возьмем любые два натурльных числа и наглядно покажем, что данное свойство справедливо. Вычислим произведение 2 · 6 . По определению произведения, нужно число 2 повторить 6 раз. Получаем: 2 · 6 = 2 + 2 + 2 + 2 + 2 + 2 = 12 . Теперь поменяем множители местами. 6 · 2 = 6 + 6 = 12 . Очевидно, переместительный закон выполняется.

На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.

Сочетательное свойство умножения натуральных чисел

Второе название для сочетательного свойства умножения — ассоциативный закон, или ассоциативное свойство. Вот его формулировка.

Сочетательный закон умножения

Умножение числа a на произведение чисел b и c равносильно умножению произведения чисел a и b на число c .

Приведем формулировку в буквенном виде:

a · b · c = a · b · c

a , b , c — любые натуральные числа. Сочетательный закон работает для трех и более натуральных чисел.

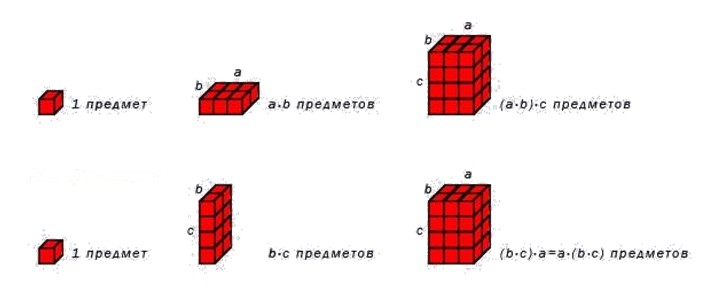
Для наглядности приведем пример. Сначала вычислим значение 4 · 3 · 2 .

4 · 3 · 2 = 4 · 6 = 4 + 4 + 4 + 4 + 4 + 4 = 24

Теперь переставим скобки и вычислим значение 4 · 3 · 2 .

4 · 3 · 2 = 12 · 2 = 12 + 12 = 24

4 · 3 · 2 = 4 · 3 · 2

Как видим, теория совпадает с практикой, и свойство справедливо.

Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.

Распределительное свойство относительно умножения

Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.

Распределительное свойство умножения относительно сложения

Умножения суммы чисел b и c на число a равносильно сумме произведений чисел a и b и a и c .

Запишем в форме буквенного выражения:

a · b + c = a · b + a · c

a , b , c — любые натуральные числа.

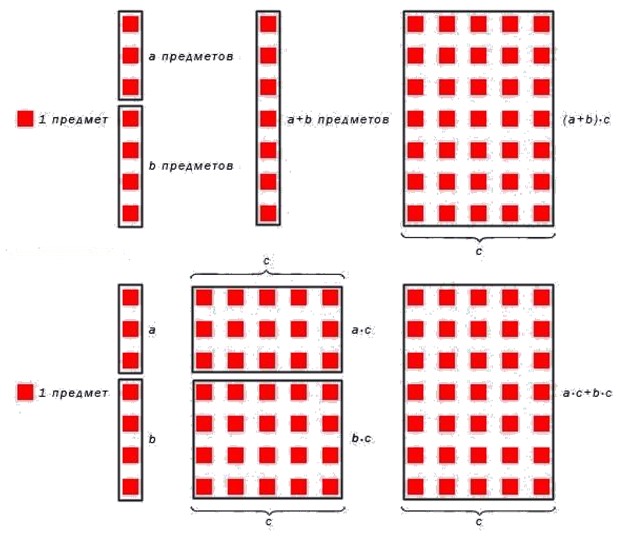
Теперь на наглядном примере покажем, как работает это свойство. Вычислим значение выражения 4 · 3 + 2 .

4 · 3 + 2 = 4 · 3 + 4 · 2 = 12 + 8 = 20

С другой стороны 4 · 3 + 2 = 4 · 5 = 20 . Справедливость распределительного свойства умножения относительно сложения показана наглядно.

Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.

Распределительное свойство умножения относительно вычитания

Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.

Распределительное свойство умножения относительно вычитания

Умножения разности чисел b и c на число a равносильно разности произведений чисел a и b и a и c .

Запишем в форме буквенного выражения:

a · b — c = a · b — a · c

a , b , c — любые натуральные числа.

В предыдущем примере заменим «плюс» на «минус» и запишем:

4 · 3 — 2 = 4 · 3 — 4 · 2 = 12 — 8 = 4

С другой стороны 4 · 3 — 2 = 4 · 1 = 4 . Таким образом, справедливость свойства умножения натуральных чисел относительно вычитания показана наглядно.

Умножение единицы на натуральное число

Умножение единицы на любое натуральное число в результате дает данное число.

По определению операции умножения, произведение чисел 1 и a равно сумме, в котором слагаемое 1 повторяется a раз.

1 · a = ∑ i = 1 a 1

Умножение натурального числа a на единицу представляет собой сумму, состоящую из одого слагаемого a . Таким образом, переместительное свойство умножения остается справедливым:

Умножение нуля на натуральное число

Число 0 не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.

Умножение нуля на натуральное число

Произведение числа 0 и любого натурального числа a равно числу 0 .

По определению, произведение 0 · a равно сумме, в которой слагаемое 0 повторяется a раз. По свойствам сложения, такая сумма равна нулю.

В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.

Напимер: 0 · 498 = 0 ; 0 · 9638854785885 = 0

Справедливо и обратное. Произведение числа на нуль также дает в результате нуль: a · 0 = 0 .

Источник