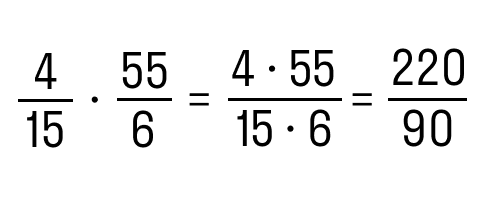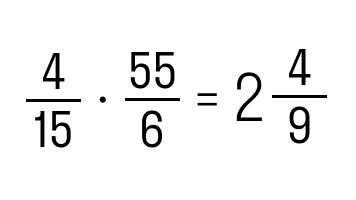Распределительный способ умножения дробей

Законы умножения

Переместительный закон умножения

Если множимое и множитель поменять местами, то произведение не изменится. Это можно легко проверить при подсчёте двумя способами числа звёздочек представленных на рисунке:

3 + 3 + 3 + 3 = 4 + 4 + 4

Так как множимое и множитель можно менять местами их ещё называют сомножителями или просто множителями.

Таким образом, для любых натуральных чисел a и b верно равенство:

выражающее переместительный закон умножения:

От перестановки сомножителей произведение не меняется.

Сочетательный закон умножения

Произведение чисел 3, 2 и 4 не изменится, если из них какие-нибудь два числа заменить их произведением:

3 · 2 · 4 = 3 · (2 · 4) = 3 · 8 = 24,

3 · 2 · 4 = (3 · 2) · 4 = 6 · 4 = 24.

Таким образом, для любых натуральных чисел a, b и c верно равенство:

выражающее сочетательный закон умножения:

Произведение не изменится, если какую-либо группу сомножителей заменить их произведением.

Распределительный закон умножения

Для любых натуральных чисел верны равенства:

выражающие распределительный закон умножения:

Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на число и полученные произведения сложить.

Распределительный закон умножения можно легко проверить при подсчёте двумя способами числа звёздочек, представленных на рисунке:

Первый: в каждом ряду расположено 3 жёлтых и 5 зелёных звёздочек, то есть всего в каждом ряду (3 + 5) звёздочек. В четырёх рядах всего (3 + 5) · 4 звёздочек.

Второй: жёлтые звёздочки расположены в четыре ряда по 3 звёздочки в каждом, то есть всего жёлтых звёздочек 3 · 4, а зелёных — 5 · 4. Всего звёздочек 3 · 4 + 5 · 4.

Кроме того, для любых натуральных чисел (если уменьшаемое больше или равно вычитаемому) верны равенства:

Например, 6 · (4 — 2) = 6 · 4 — 6 · 2.

Переход от умножения:

соответственно к сложению и вычитанию:

называется раскрытием скобок.

Переход от сложения и вычитания:

называется вынесением общего множителя за скобки.

Источник

Урок 16 Бесплатно Применение распределительного свойства умножения

В этом уроке мы узнаем, как умножать смешанное число на натуральное, и разберем, как использовать распределительное свойство умножения для рационализации вычислений с обыкновенными дробями и смешанными числами.

Распределительное свойство умножения

Это свойство говорит нам о том, что если необходимо умножить одно число, назовем его a, на сумму двух других чисел, обозначим их b и c, то ответом будет сумма двух произведений: произведения a и b и произведения a и c

Напомним, коммутативное свойство — это научный термин для обычного правила, которое гласит, что перемена мест слагаемых (или множителей) не влияет на результат.

Вторая строка говорит о том же самом, что и первая; просто показывает, что коммутативное свойство умножения работает и в этом случае.

Умножение смешанного числа на натуральное используя распределительной свойство

В уроке «Умножение дробей» мы уже касались этих моментов. Теперь рассмотрим их более подробно.

Самый простой способ умножения смешанного числа на натуральное заключается в том, чтобы перевести смешанное число в натуральную дробь, домножив целую часть на знаменатель и прибавив его к числителю, а далее домножить полученную неправильную дробь на натуральное число, перемножив числитель дроби и натуральное число.

Это и будет результатом.

Пример:

Этот пример нам показывает, что даже такая простая операция, как умножение на 2, приводит нас к множеству умножений, сложений и даже делению. Для больших чисел такой путь неудобен. Стоит только представить, что целая часть смешанного числа будет больше 100, и знаменатель также также весьма сложный, то мы получим операции, которые с трудом делаются в уме.

Здесь нас выручит распределительное свойство.

Если представить \(\mathbf<43\frac<1><3>>\) как сумму его целой и дробной частей, то есть

\(\mathbf<43\frac<1><3>=43+\frac<1><3>>\), то нам нужно будет в дальнейшем умножать только 43 и \(\mathbf<\frac<1><3>>\), что значительно проще.

Посмотрим, как это все будет выглядеть целиком:

Можно заметить, что несмотря на то, что мы удлинили запись выражения, сами вычисления стали проще.

Может возникнуть необходимость выделения целой части, про это забывать нельзя. Но даже в таком случае делимое будет значительно меньше, чем если бы мы выносили целую часть из произведения, полученного классическим способом.

Пример:

Пройти тест и получить оценку можно после входа или регистрации

Источник

Свойства умножения и деления

О чем эта статья:

Свойства умножения

Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.

Узнаем, какие бывают свойства умножения и как их применять.

Переместительное свойство умножения

От перестановки мест множителей произведение не меняется.

То есть, для любых чисел a и b верно равенство: a * b = b * a.

Это свойство можно применять к произведениям, в которых больше двух множителей.

• 6 * 5 = 5 * 6 = 30;
• 4 * 2 * 3 = 3 * 2 * 4 = 24.

Сочетательное свойство умножения

Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.

То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).

3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30

3 * 2 * 5 = (3 * 2) * 5 = 6 * 5 = 30.

Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.

Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.

Распределительное свойство умножения относительно сложения

Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.

То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.

Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.

В обратную сторону распределительное свойство умножения относительно сложения звучит так:

Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Распределительное свойство умножения относительно вычитания

Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.

То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.

В обратную сторону распределительное свойство умножения относительно вычитания звучит так:

Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Свойство нуля при умножении

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.

Свойство единицы при умножении

Если умножить любое целое число на единицу, то в результате получится это же число.

То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.

Свойства деления

Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.

Основные свойства деления целых чисел

1. Деление на нуль невозможно.
2. Деление нуля на число: 0 : a = 0.
3. Деление равных чисел: a : a = 1.
4. Деление на единицу: a : 1 = a.
5. Для деления переместительное свойства не выполняется: a : b ≠ b : a.
6. Деление суммы и разности на число: (a ± b) : c = (a : c) ± (b : c).
7. Деление произведения на число:
   (a * b) : c = (a : c) * b, если a делится на c;
   (a * b) : c = a * (b : с), если b делится на c;
   (a * b) : c = a * (b : с) = (a : c) * b, если a и b делятся на c.
8. Деление числа на произведение:
   a : (b * c) = (a : b) * (1 : c) = (a : c) * (1 : b).

И еще одно важное свойство деления, которое проходят в 5 классе:

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.

Применим свойства деления на практике.

Пример 1

Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?

Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.

Пример 2

Вычислить: 500 * (100 : 5).

Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.

Ответ: 500 * (100 : 5) = 10000.

Пример 3

Упростить выражение: 27a – 16a.

Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 — 16) = a * 11 = 11a.

Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.

Источник

Умножение дробей: теория и практика

О чем эта статья:

5 класс, 6 класс

Понятие дроби

Дробь — одна из форм представления числа в математике. Это запись, в которой a и b являются числами или выражениями. Существует два формата записи:

• обыкновенный вид — 1/2 или a/b,
• десятичный вид — 0,5.

Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление — в 5 классе уже это знают.

Дроби могут быть двух видов:

1. Числовые — состоят из чисел, например, 5/9 или (1,5 — 0,2)/15.
2. Алгебраические — состоят из переменных, например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя:

Неправильной — ту, у которой числитель больше знаменателя или равен ему:

Такое число называют смешанным, читают как «пять целых одна четвертая», а записывают так: 5 1\4.

Основные правила дробей

• Если делитель равен нулю — у дроби нет значения
• Дробь равна нулю, если числитель равен нулю, а знаменатель — нет
• Две дроби a/b и c/d называют равными, если a * d = b * c.
• Если числитель и знаменатель умножить или разделить на одно и то же натуральное число — получится равная ей дробь.

Умножение дробных чисел

Рассмотрим несколько вариантов умножения обыкновенных дробей.

Как умножить дробь на дробь

Числитель равен произведению числителей обеих дробей, а знаменатель равен произведению знаменателей:

Важно проверить возможность сокращения — так решать будет легче:

Как умножить смешанные дроби

Преобразовать смешанные числа в неправильные, перемножить числители и знаменатели, при необходимости сократить и перевести в смешанную дробь.

Как умножить дробь на натуральное число

Метод 1. Числитель умножить на натуральное число, а знаменатель оставить без изменения. Если в результате произведения получилась неправильная дробь, нужно выделить целую часть, то есть превратить неправильную в смешанную.

Метод 2. Знаменатель разделить на натуральное число, а числитель оставить прежним.

Этот способ будет удобнее предыдущего, если знаменатель делится на натуральное число без остатка.

Решение задач

Ребятам в 5 и 6 классе нужно практиковаться как можно чаще, чтобы решать такие примеры быстро и легко.

Задание 1. Выполнить умножение 2/17 на 5.

Как решаем: перемножим делимое и натуральное число.

Ответ:

Задание 2. Выполнить умножение 4/15 и 55/6.

Как решаем:

• перемножим числители между собой и знаменатели соответственно
  

• сократим полученное

• выделим целую часть

Ответ:

Задание 3. Выполнить умножение одной целой трех седьмых на шесть.

Как решаем:

• переводим смешанное число в неправильную дробь,
• умножаем делимое на натуральное число,
• сократим полученное,
• преобразуем в смешанное число.

Ответ:

Если вопрос не ждет и ответ нужно получить как можно быстрее, можно использовать онлайн калькулятор. Умножение будет быстрым и точным:

Источник