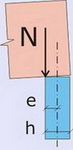
Расчетная длина колонны (стены)

При расчете колонн или стоек ферм постоянного по длине сечения требуется помимо всего прочего знать расчетную длину колонны или стойки. Знание расчетной длины также необходимо при расчете участка стены на прочность. При этом не имеет решающего значения, из какого материала изготовлена или проектируется колонна, стойка или стена. Ни дерево ни металл ни бетон ни пластик на значение расчетной длины почти не влияют. А вот способ закрепления рассчитываемой конструкции на опорах или на опоре влияет на значение расчетной длины весьма значительно.

Так, например, для колонны с высотой Н с жестким защемлением только на нижней опоре, другими словами, глубоко заделанной в фундамент или крепящейся к фундаменту анкерными болтами, расчетная длина будет в 4 раза больше, чем колонны с такой же высотой Н и жестким защемлением на нижней опоре, но дополнительно имеющей жесткое защемление сверху. Почему? Сейчас попробуем разобраться.

Теоретически все выглядит до смешного просто: чтобы определить расчетную длину, нужно умножить высоту (реальную длину) колонны, стойки или рассчитываемого участка стены на коэффициент μ, учитывающий способ закрепления на опорах:

l_ef = μl (233.1.1)

l_o = μH (233.1.2)

При расчете металлических конструкций принято обозначение расчетной длины l_ef, при расчете каменных и армокаменных конструкций расчетная длина обозначается как l_o, да и высота колонны может обозначаться как угодно, сути дела это не меняет. В любом случае для дальнейших расчетов нужно определить значение коэффициента μ. Если ситуация с закреплением на опорах пока не известна или нет большого желания разбираться в тонкостях различий, то лучше принять значение μ = 2 и смело считать дальше. Это практически максимальное возможное значение коэффициента и самое страшное, что может случиться с Вашей конструкцией в этом случае — это относительно небольшой запас по прочности.

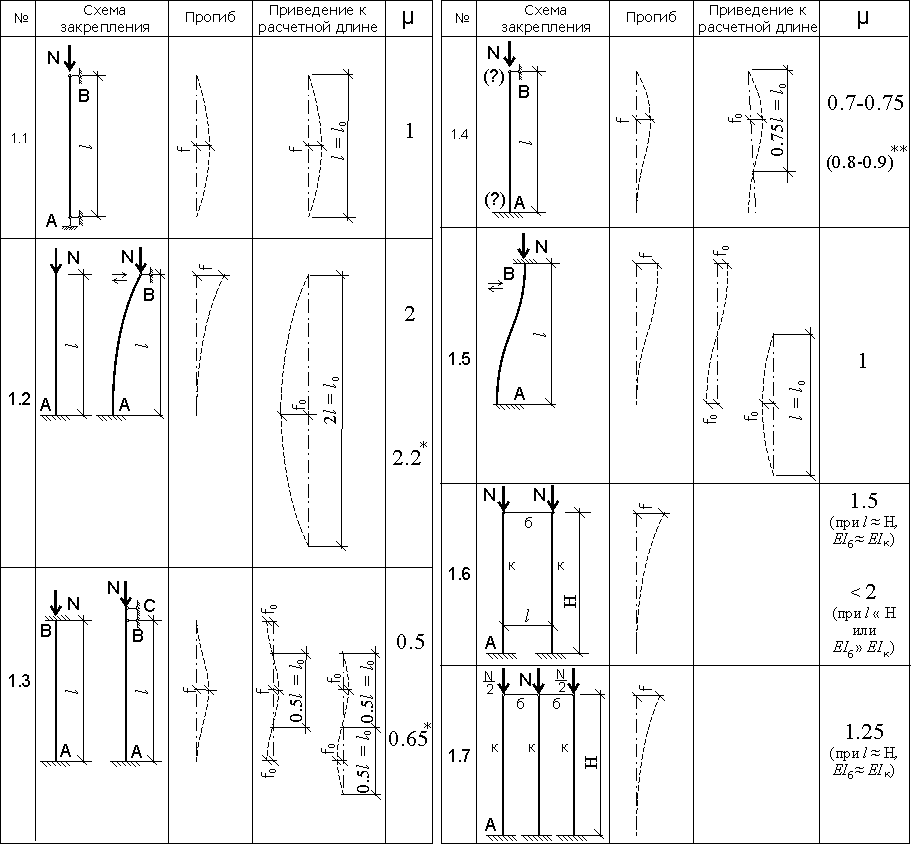
Если же Вы чувствуете в себе силы разобраться в нюансах закрепления, то милости просим. Проще всего это сделать по следующей таблице:

Таблица 233.1. Значение коэффициента μ при нагрузке, приложенной к верху (оголовку) колонны, стойки, стены.

1* — Рекомендованные значения для расчетов деревянных конструкций

2** — Если защемление на опоре недостаточно жесткое или опоры не являются чисто шарнирными.

3. При действии только равномерно распределенной нагрузки по всей длине колонны — от собственного веса колонны или от листов зашивки каркаса стены — значение коэффициента μ уменьшается в связи со смещением точки приложения сосредоточенной нагрузки.

При шарнирных опорах:

• Для деревянных конструкций рекомендуется использовать понижающий коэффициент 0.73
• для каменных и армокаменных конструкций — 0.75
• для стальных и железобетонных конструкций — 0.725.

При жестком защемлении только на верхней опоре:

• для деревянных и железобетонных конструкций используется коэффициент μ = 1.2,
• для каменных и армокаменных конструкций — μ = 1.5
• для стальных конструкций — μ = 1.12.

Как видим, теоретическая простота на деле распыляется на несколько вариантов. Даже при наличии всего двух вариантов вероятность выбора наугад правильного варианта составляет около 50%. При 7 представленных вариантах вероятность отгадывания правильного варианта падает значительно, поэтому мы не будем полагаться на волю случая, а более подробно рассмотрим указанные варианты.

Любая сжимаемая колонна или стойка или стена будет деформироваться, причем чем более неоднородным будет материал конструкции, чем сильнее его центральная ось будет отклонена от прямой линии и чем больше при этом соотношение длины конструкции к ширине или высоте поперечного сечения, тем больше вероятность того, что конструкция не сожмется как пружина, а выгнется как палка, на которую давишь, впрочем и очень длинную пружину тоже равномерно сжать не удастся и она тоже выгнется.

В таблице изменение положения центральной оси стержня показано пунктиром. Это изменение, описываемое прогибом f, приведет к появлению эксцентриситета приложения нагрузки, а значит и внутренние напряжения в рассматриваемом сечении изогнутой конструкции будут больше, чем в прямолинейной, так как появится момент от эксцентриситета приложения нагрузки. В свою очередь этот момент будет вызывать дополнительный прогиб и увеличение нормальных напряжений, дополнительный прогиб — еще дополнительный момент и так до бесконечности или до тех пор, пока колонна не разрушится или не потеряет устойчивость (более подробно и наглядно данный процесс рассматривается отдельно). Причем потеря устойчивости скорее всего произойдет относительно той оси, относительно которой соотношение длины к конструкции к одному из размеров поперечного сечения наибольшее. И хотя в данной статье рассматриваются некие стержни без привязки к каким-либо осям, но помнить об этом все-таки нужно.

Наиболее опасным с точки зрения потери устойчивости для стержней на двух шарнирных опорах постоянного по всей длине сечения является поперечное сечение посредине длины стержня. В этом рассчитываемые на сжатие стержни похожи на симметрично или равномерно загруженные балки. В принципе если исхитриться и наклонить голову на 90 градусов и посмотреть на таблицу, то колонну от балки не отличишь. Как и для балки, для сжатой стойки или колонны очень важной характеристикой является величина прогиба, ведь чем больше прогиб, тем меньше несущая способность конструкции. Вот только как быстро определить этот прогиб? Ведь эпюры прогиба, характеризующие изменение положения центров тяжести поперечных сечений относительно центральной оси, при различных способах закрепления на опорах разные. И тогда какой-то умный человек, фамилии которого я не знаю (возможно это был математик Эйлер, впервые рассчитавший значение критической сжимающей силы, но утверждать не буду), придумал способ приведения различных расчетных схем к единому знаменателю, реализованный в таблице 233.1. Суть этого способа сводится к тому, чтобы одно из возможных закреплений балки взять за основу, а все остальные варианты закрепления стержней на опорах привести к основному использованием соответствующего коэффициента.

В таблице 233.1 такой основой является колонна с шарнирными опорами (№1.1) , однако использовать такую расчетную длину можно только для стоек ферм или для колонн имеющих диагональные связи в плоскости расчета или для колонн каркаса имеющего соответствующую диафрагму жесткости. Во всех остальных случаях значение расчетной длины будет больше и виной тому странное желание человека строить здания прямоугольной формы. Как известно, каркас, представляющий собой прямоугольник — штука очень ненадежная — геометрической неизменяемостью не обладает, а потому может запросто сложиться, как детская игрушка и потому в каркасных зданиях диагональные связи между колоннами или диафрагмы жесткости обязательны. В домах с несущими стенами эти самые несущие стены и выполняют дополнительно функцию диафрагм жесткости, поэтому любой дом, имеющий 4 стены некоторой определенной толщины намного прочнее, чем отдельно стоящая стена такой же толщины. Поэтому при определении коэффициента μ (или расчетной длины) эту особенность нужно учитывать. В связи с этим

Наиболее заслуживающей доверия расчетной схемой является расчетная схема для колонны с жестким защемлением на нижней опоре (№1.2) . Такая расчетная схема подходит для всех отдельно стоящих колонн, а также может применяться при колонн однопролетного и даже двухпролетного каркаса при соблюдении условий указанных для схемы №1.6.

Расчетная схема №1.3 — самый лакомый кусок для начинающего проектировщика, так как позволяет уменьшить расчетную длину в четыре раза по сравнению с расчетной схемой №1.2. Однако применять эту схему можно лишь для сварных металлоконструкций и железобетонных конструкций, в которых опорные узлы отдельно просчитываются на нагрузки, или для отдельных участков колонн или стен, изготовленных из других материалов, поэтому на эту расчетную схему лучше вообще не смотреть. К тому же даже незначительная подвижность жесткой опоры В (расчетная схема 1.5) в плоскости, перпендикулярной оси стержня сразу вдвое увеличивает расчетную длину.

Расчетная схема №1.4 — это более реальный вариант. Такая схема применима для кирпичных и каменных стен, а также для колонн, имеющих диафрагмы жесткости в двух плоскостях. Если Вы на 100% не уверены в том, что верхняя опора будет абсолютно неподвижной, то можно принимать расчетную длину по расчетной схеме №1.5 . Впрочем при расчете каменных стен следует среди прочего учитывать этажность и вид перекрытий.

Для колонн из древесины, металла и других материалов, на которые будут опираться балки перекрытия, на которые в свою очередь будет монтироваться перекрытие лучше использовать расчетные схемы №1.6 и №1.7 .

Для стальных колонн — вертикальных элементов рам, при отсутствии диафрагм жесткости значение коэффициента μ следует определять согласно таблицы 17.а СНиП II-23-81*(1990) «Стальные конструкции».

Вот в принципе и все.

На этом пока все.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630

Категории:

• Расчет конструкций . Расчетные предпосылки
• Расчет конструкций . Основы строймеха и сопромата . Колонны

Оценка пользователей: 8.3 (голосов: 3) Переходов на сайт: 32756 Комментарии:

Доброго дня, Доктор!
Помогите решить вопросик. Имеется деревянный двухэтажный дом,брус 15х15, размер дома 8х9м внутри несущие стены делят его практически на четыре равные части.Есть идея выпилить одну стену на первом этаже и одну на втором. Как рассчитать максимально возможную величину проема, для того что бы эта великолепная конструкция не рухнула, крышу не повело и вообще не навредить строению. Есть какие либо формулы для расчета «от обратного».
Буду весьма признательна за пояснения

Формул всяких много есть. Вот только в вашем случае лучше пригласить инженера, чтобы он по месту определил конструктивную схему вашего здания и предложил оптимальный вариант.

Добрый день, док!
Почему у Вас в расчетах для деревянных конструкций часто расчетная длина равна фактической, т.е. коэффициент равен 1? Ведь там больше подойдет схема 1.6/1.7? Или это поправка на диафрагму жесткости такая? Какую схему целесообразно применить для расчёта стойки в каркасной стене прямоугольного/квадратного дома?

Насколько я помню, у меня только один пример расчета деревянной стойки — части стропильной системы. И для этой стойки в плоскости стропильных ног неподвижность верхней и нижней опоры достигается геометрией (так как треугольник — геометрически неизменяемая система), а из плоскости стропильных ног — обрешеткой и настилом по обрешетке, а также парой подкосов.
Для стойки — части каркасной стены выбор коэффициента будет зависеть от множества факторов, в частности от устройства перекрытия и узлов сопряжения перекрытия со стенами, а также от методов закрепления обшивки стен. При наиболее неблагоприятных вариантах коэффициент действительно можно принимать по схеме 1.7, но для этого стойки на нижней опоре должны быть соответствующим образом защемлены. Расчетная схема 1.6 для стоек каркасного дома маловероятна, но возможна. В принципе, как я уже неоднократно говорил, если не знаете как правильно считать, считайте по максимуму, в данном случае принимайте максимально возможное значение коэффициента ?.

Как определить расчетную длину торцевой самонесущей стены 4-х этажного дома, если плиты перекрытий на нее совсем не заходят. Расчетная схема 1.1 или 1.2?

Такая стена будет иметь перевязку с наружными, возможно и с внутренними стенами, поэтому рассматривать ее по всей высоте, как отдельно стоящую колонну будет не совсем корректно. Тем не менее для упрощенных расчетов можете воспользоваться расчетной схемой 1.1.

А для расчета опор(ног) козлового крана какая схема ближе? Опоры при виде сбоку имеют угол Крепление опор вверху и внизу стяжками на болтах.

Если крепления опор (болты) рассчитаны на возникающие усилия и обеспечивают неподвижность, то можно воспользоваться схемой 1.3. Но для надежности лучше воспользоваться схемой 1.1. А угол наклона опор козлового крана влияет только на определение вертикальной составляющей нагрузки. Примерно так.

Добрый день! Подскажите, может ли расчетная длина среднего участка двухступенчатой колонны быть в три раза больше чем общая геометрическая высота колонны? (считаю по СП «Стальные конструкции», приложение И)

Вы представили слишком мало данных. Но теоретически, при жестком защемлении внизу и свободном верхнем конце это возможно. Тут главное не забывать, что любой рассматриваемый участок колонны по-прежнему остается частью общей колонны, просто рассматривается отдельно, в зависимости от имеющихся геометрических характеристик.
В то же время, если в районе ступеней имеются дополнительные горизонтальные связи, то это позволяет рассматривать каждый участок колонны отдельно и тогда расчетная длина каждого участка будет меньше или равна реальной высоте участка. Впрочем тут нужно смотреть на ситуацию в целом. Как я уже говорил данных для анализа вы представили не достаточно.

Подскажите расчетную длину колонны.Заранее спасибо, Dr.LOM.

Какой именно колонны?

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник

Расчет металлических колонн

Часто люди, делающие во дворе крытый навес для автомобиля или для защиты от солнца и атмосферных осадков, сечение стоек, на которые будет опираться навес, не рассчитывают, а подбирают сечение на глаз или проконсультировавшись у соседа.

Понять их можно, нагрузки на стойки, в данном случае являющиеся колоннами, не ахти какие большие, объем выполняемых работ тоже не громадный, да и внешний вид колонн иногда намного важнее их несущей способности, поэтому даже если колонны будут сделаны с многократным запасом по прочности — большой беды в этом нет. Тем более, что на поиски простой и внятной информации о расчете сплошных колонн можно потратить бесконечное количество времени без какого-либо результата — разобраться в примерах расчета колонн для производственных зданий с приложением нагрузки в нескольких уровнях без хороших знаний сопромата практически невозможно, а заказ расчета колонны в инженерной организации может свести всю ожидаемую экономию к нулю.

Данная статья написана с целью хоть немного изменить существующее положение дел и является попыткой максимально просто изложить основные этапы расчета металлической колонны, не более того. Все основные требования по расчету металлических колонн можно найти в СНиП II-23-81 (1990).

Общие положения

С теоретической точки зрения расчет центрально-сжатого элемента, каковым является колонна, или стойка в ферме, настолько прост, что даже неудобно об этом говорить. Достаточно разделить нагрузку на расчетное сопротивление стали, из которой будет изготавливаться колонна — все. В математическом выражении это выглядит так:

F — требуемая площадь сечения колонны, см²

N — сосредоточенная нагрузка, прилагаемая к центру тяжести поперечного сечения колонны, кг;

R_y — расчетное сопротивление металла растяжению, сжатию и изгибу по пределу текучести, кг/см&sup2. Значение расчетного сопротивления можно определить по соответствующей таблице.

Как видим, уровень сложности задачи относится ко второму, максимум к третьему классу начальной школы. Однако на практике все далеко не так просто, как в теории, по ряду причин:

1. Приложить сосредоточенную нагрузку точно к центру тяжести поперечного сечения колонны можно только теоретически. В реальности нагрузка всегда будет распределенной и еще будет некоторый эксцентриситет приложения приведенной сосредоточенной нагрузки. А раз есть эксцентриситет, значит есть продольный изгибающий момент действующий в поперечном сечении колонны.

2. Центры тяжести поперечных сечений колонны расположены на одной прямой — центральной оси, тоже только теоретически. На практике из-за неоднородности металла и различных дефектов центры тяжести поперечных сечений могут быть смещены относительно центральной оси. А это значит, что расчет нужно производить по сечению, центр тяжести которого максимально удален от центральной оси, из-за чего эксцентриситет действия силы для этого сечения максимальный.

3. Колонна может иметь не прямолинейную форму, а быть немного изогнутой в результате заводской или монтажной деформации а это значит, что поперечные сечения в средней части колонны будут иметь наибольший эксцентриситет приложения нагрузки.

4. Колонна может быть установлена с отклонениями от вертикали, а это значит, что вертикально действующая нагрузка может создавать дополнительный изгибающий момент, максимальный в нижней части колонны, а если точнее, в месте крепления к фундаменту, впрочем это актуально, только для отдельно стоящих колонн.

5. Под действием приложенных к ней нагрузок колонна может деформироваться, а это значит, что опять появится эксцентриситет приложения нагрузки и как следствие дополнительный изгибающий момент.

6. В зависимости от того, как именно закреплена колонна, зависит значение дополнительного изгибающего момента внизу и в средней части колонны.

Все это приводит к появлению продольного изгиба и влияние это изгиба при расчетах нужно как-то учитывать.

Естественно, что рассчитать вышеуказанные отклонения для конструкции, которая еще только проектируется, практически невозможно — расчет будет очень долгим, сложным, а результат все равно сомнительным. А вот ввести в формулу (1.1) некий коэффициент, который бы учел вышеизложенные факторы, очень даже можно. Таким коэффициентом является φ — коэффициент продольного изгиба. Формула, в которой используется данный коэффициент, выглядит так:

Значение φ всегда меньше единицы, это означает, что сечение колонны всегда будет больше, чем если просто посчитать по формуле (1.1), это я к тому, что сейчас начнется самое интересное и помнить, что φ всегда меньше единицы — не помешает. Для предварительных расчетов можно использовать значение φ в пределах 0,5-0,8. Значение φ зависит от марки стали и гибкости колонны λ:

l_ef — расчетная длина колонны. Расчетная и реальная длина колонны — разные понятия. Расчетная длина колонны зависит от способа закрепления концов колонны и определяется с помощью коэффициента μ:

l — реальная длина колонны, см;

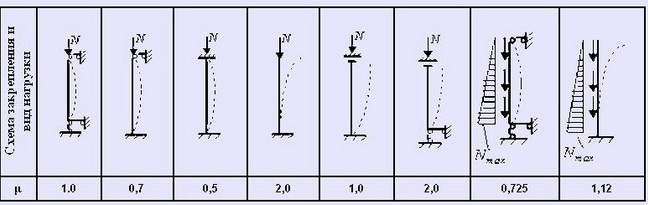
μ — коэффициент, учитывающий способ закрепления концов колонны. Значение коэффициента можно определить по следующей таблице:

Таблица 1. Коэффициенты μ для определения расчетных длин колонн и стоек постоянного сечения (согласно СНиП II-23-81 (1990))

Как видим, значение коэффициента μ изменяется в несколько раз в зависимости от способа закрепления колонны и тут главная сложность в том, какую расчетную схему выбрать. Если не знаете, какая схема закрепления соответствует Вашим условиям, то принимайте значение коэффициента μ=2. Значение коэффициента μ=2 принимается в основном для отдельно стоящих колон, наглядный пример отдельно стоящей колонны — фонарный столб. Значение коэффициента μ=1-2 можно принимать для колонн навесов, на которые опираются балки без жесткого крепления к колонне. Данную расчетную схему можно принимать, когда балки навеса будут не жестко крепиться к колоннам и когда балки будут иметь относительно большой прогиб. Если на колонну будут опираться фермы, жестко прикрепленные к колонне сваркой, то можно принимать значение коэффициента μ=0,5-1. Если между колоннами будут диагональные связи, то можно принимать значение коэффициента μ=0,7 при нежестком креплении диагональных связей или 0,5 при жестком креплении. Однако такие диафрагмы жесткости не всегда бывают в 2 плоскостях и потому использовать такие значения коэффициента нужно осторожно. При расчете стоек ферм используется коэффициент μ=0,5-1 в зависимости от метода закрепления стоек.

Значение коэффициента гибкости приблизительно показывает отношение расчетной длины колонны к высоте или ширине поперечного сечения. Т.е. чем больше значение λ, тем меньше ширина или высота поперечного сечения колонны и соответственно тем больший запас по сечению потребуется при одной и той же длине колонны, но об этом чуть позже.

Теперь когда мы определили коэффициент μ, можно вычислить расчетную длину колонны по формуле (1.4), а для того, чтобы узнать значение гибкости колонны, нужно знать радиус инерции сечения колонны i:

(1.5)

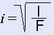
где I — момент инерции поперечного сечения относительно одной из осей, и тут начинается самое интересное, потому как в ходе решения задачи мы как раз и должны определить необходимую площадь сечения колонны F, но этого мало, оказывается, мы еще должны знать значение момента инерции. Так как мы не знаем ни того, ни другого, то решение задачи выполняется в несколько этапов.

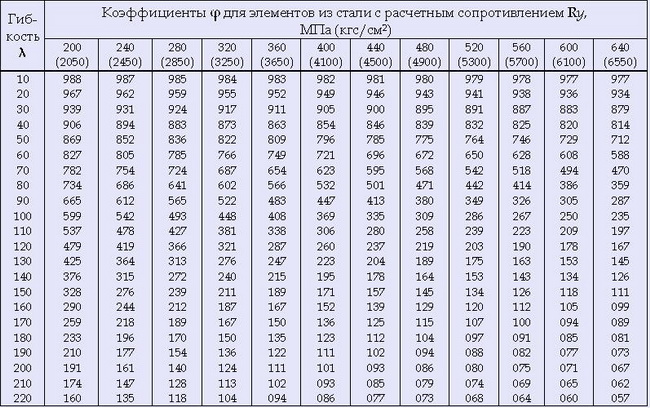
На предварительном этапе обычно принимается значение λ в пределах 90-60, для колонн с относительно небольшой нагрузкой можно принимать λ = 150-120 (максимальное значение для колонн — 180, значения предельной гибкости для других элементов можно узнать по таблице 19* СНиП II-23-81 (1990). Затем по Таблице 2 определяется значение коэффициента гибкости φ:

Таблица 2. Коэффициенты продольного изгиба φ центрально-сжатых элементов.

Примечание: значения коэффициента φ в таблице увеличены в 1000 раз.

После этого определяется требуемый радиус инерции поперечного сечения, путем преобразования формулы (1.3):

По сортаменту подбирается прокатный профиль с соответствующим значением радиуса инерции. В отличие от изгибаемых элементов, где сечение подбирается только по одной оси, так как нагрузка действует только в одной плоскости, в центрально сжатых колоннах продольный изгиб может произойти относительно любой из осей и потому чем ближе значение I_z к I_y, тем лучше, другими словами наиболее предпочтительны профили круглого или квадратного сечения. Ну а теперь попробуем определить сечение колонны на основе полученных знаний.

Пример расчета металлической центрально-сжатой колонны

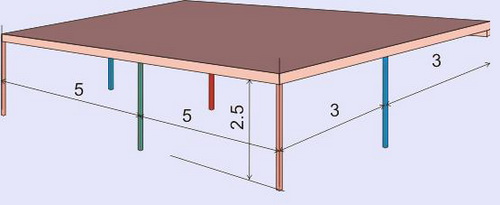
Имеется: желание сделать навес возле дома приблизительно следующего вида:

В данном случае единственной центрально-сжатой колонной при любых условиях закрепления и при равномерно распределенной нагрузке будет колонна, показанная на рисунке красным цветом. Кроме того и нагрузка на эту колонну будет максимальной. Колонны, обозначенные на рисунке синим и зеленым цветом, можно рассматривать как центрально-сжатые, только при соответствующем конструктивном решении и равномерно-распределенной нагрузке, колонны, обозначенные оранжевым цветом, будут или центрально сжатыми или внецентренно-сжатыми или стойками рамы, рассчитываемой отдельно. В данном примере мы рассчитаем сечение колонны, обозначенной красным цветом. Для расчетов примем постоянную нагрузку от собственного веса навеса 100 кг/м&sup2 и временную нагрузку 100 кг/м&sup2 от снегового покрова.

2.1. Таким образом сосредоточенная нагрузка на колонну, обозначенную красным цветом, составит:

N = (100+100)·5·3 = 3000 кг

2.2. Принимаем предварительно значение λ = 100, тогда по таблице 2 коэффициент изгиба φ = 0,599 (для стали с расчетной прочностью 200 МПа, данное значение принято для обеспечения дополнительного запаса по прочности), тогда требуемая площадь сечения колонны:

F = 3000/(0,599·2050) = 2,44 см&sup2

2.3. По таблице 1 принимаем значение μ = 1 (так как кровельное покрытие из профилированного настила, должным образом закрепленное, будет обеспечивать жесткость конструкции в плоскости, параллельной плоскости стены, а в перпендикулярной плоскости относительную неподвижность верхней точки колонны будет обеспечивать крепление стропил к стене), тогда радиус инерции

2.4. По сортаменту для квадратных профильных труб данным требованиям удовлетворяет профиль с размерами поперечного сечения 70х70 мм с толщиной стенки 2 мм, имеющий радиус инерции 2,76 см. Площадь сечения такого профиля 5,34 см&sup2. Это намного больше, чем требуется по расчету.

2.5.1. Мы можем увеличить гибкость колонны, при этом требуемый радиус инерции уменьшится. Например, при λ = 130 коэффициент изгиба φ = 0,425, тогда требуемая площадь сечения колонны:

F = 3000/(0,425·2050) = 3,44 см&sup2

2.5.3. По сортаменту для квадратных профильных труб данным требованиям удовлетворяет профиль с размерами поперечного сечения 50х50 мм с толщиной стенки 2 мм, имеющий радиус инерции 1,95 см. Площадь сечения такого профиля 3,74 см&sup2, момент сопротивления для этого профиля составляет 5,66 см&sup3.

Вместо квадратных профильных труб можно использовать равнополочный уголок, швеллер, двутавр, обычную трубу. Если расчетное сопротивление стали выбранного профиля больше 220 МПа, то можно пересчитать сечение колонны. Вот в принципе и все, что касается расчета металлических центрально-сжатых колонн.

Расчет внецентренно-сжатой колонны

Тут конечно же возникает вопрос: а как рассчитать остальные колонны? Ответ на этот вопрос сильно зависит от способа крепления навеса к колоннам. Если балки навеса будут жестко крепиться к колоннам, то при этом будет образована достаточно сложная статически неопределимая рама и тогда колонны следует рассматривать как часть этой рамы и рассчитывать сечение колонн дополнительно на действие поперечного изгибающего момента, мы же далее рассмотрим ситуацию когда колонны, показанные на рисунке, соединены с навесом шарнирно (колонну, обозначенную красным цветом, мы больше не рассматриваем). Например оголовок колонн имеет опорную площадку — металлическую пластину с отверстиями для болтового крепления балок навеса. По разным причинам нагрузка на такие колонны может передаваться с достаточно большим эксцентриситетом:

Балка, показанная на рисунке, бежевым цветом, под воздействием нагрузки немного прогнется и это приведет к тому, что нагрузка на колонну будет передаваться не по центру тяжести сечения колонны, а с эксцентриситетом е и при расчете крайних колонн этот эксцентриситет нужно учитывать. Случаев внецентренного нагружения колонн и возможных поперечных сечений колонн существует великое множество, описываемое соответствующими формулами для расчета. В нашем случае для проверки сечения внецентренно-сжатой колонны мы воспользуемся одной из самых простых:

В данном случае, когда сечение самой нагруженной колонны мы уже определили, нам достаточно проверить, подходит ли такое сечение для остальных колонн по той причине, что задачи строить сталелитейный завод у нас нет, а мы просто рассчитываем колонны для навеса, которые будут все одинакового сечения из соображений унификации.

Формула (3.1) после простейших преобразований, примет следующий вид:

так как М_z=N·e_z, почему значение момента именно такое и что такое момент сопротивления W, достаточно подробно объясняется в отдельной статье.

Сосредоточенная нагрузка N на колонны, обозначенные на рисунке синим и зеленым цветом, составит 1500 кг. Проверяем требуемое сечение при такой нагрузке и ранее определенном φ = 0,425

F = (1500/2050)(1/0,425 + 2,5·3,74/5,66) = 0,7317·(2,353 + 1,652) = 2,93 см&sup2

Кроме того, формула (3.2) позволяет определить максимальный эксцентриситет, который выдержит уже рассчитанная колонна, в данном случае максимальный эксцентриситет составит 4,17 см.

Требуемое сечение 2,93 см&sup2 меньше принятого 3,74 см&sup2, а потому квадратную профильную трубу с размерами поперечного сечения 50х50 мм с толщиной стенки 2 мм можно использовать и для крайних колонн.

Расчет внецентренно-сжатой колонны по условной гибкости

Как ни странно, но для подбора сечения внецентренно-сжатой колонны — сплошного стержня есть еще более простая формула:

φ_е — коэффициент продольного изгиба, зависящий от эксцентриситета, его можно было бы назвать эксцентриситетным коэффициентом продольного прогиба, чтобы не путать с коэффициентом продольного прогиба φ. Однако расчет по этой формуле может оказаться более длительным чем по формуле (3.2). Чтобы определить коэффициент φ_е необходимо все равно знать значение выражения e_z·F/W_z — которое мы встречали в формуле (3.2). Это выражение называется относительным эксцентриситетом и обозначается m:

После этого определяется приведенный относительный эксцентриситет:

h — это не высота сечения, а коэффициент, определяемый по таблице 73 СНиПа II-23-81. Просто скажу, что значение коэффициента h изменяется в пределах от 1 до 1,4, для большинства простых расчетов можно использовать h = 1,1-1,2.

После этого нужно определить условную гибкость колонны λ¯:

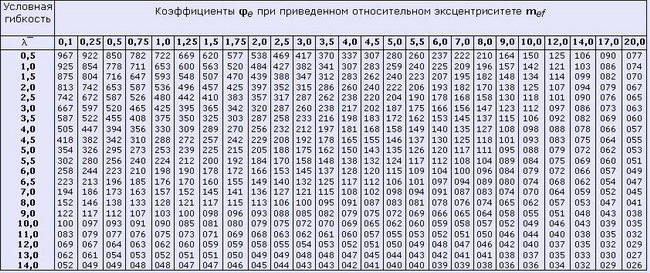
и только после этого по таблице 3 определить значение φ_е:

Таблица 3. Коэффициенты φ_e для проверки устойчивости внецентренно-сжатых (сжато-изгибаемых) сплошностенчатых стержней в плоскости действия момента, совпадающей с плоскостью симметрии.

1. Значения коэффициента φ_е увеличены в 1000 раз.
2. Значение φ_е следует принимать не более φ.

Теперь для наглядности проверим сечение колонн, нагруженных с эксцентриситетом, по формуле (4.1):

4.1. Сосредоточенная нагрузка на колонны, обозначенные синим и зеленым цветом, составит:

N = (100+100)·5·3/2 = 1500 кг

Эксцентриситет приложения нагрузки е = 2,5 см, коэффициент продольного изгиба φ = 0,425.

4.2. Значение относительного эксцентриситета мы уже определяли:

4.3. Теперь определим значение приведенного коэффициента m_ef:

4.4. Условная гибкость при принятом нами коэффициенте гибкости λ = 130, прочности стали R_y = 200 МПа и модуле упругости Е = 200000 МПа составит:

λ¯ = 130√‾(200/200000) = 4,11

4.5. По таблице 3 определяем значение коэффициента φ_е ≈ 0,249

4.6. Определяем требуемое сечение колонны:

F = 1500/(0,249·2050) = 2,94 см&sup2

Напомню, что при определении площади сечения колонны по формуле (3.1) мы получили почти такой же результат.

Совет: Чтобы нагрузка от навеса передавалась с минимальным эксцентриситетом, в опорной части балки делается специальная площадка. Если балка металлическая, из прокатного профиля, то обычно достаточно приварить к нижней полке балки кусок арматуры.

Источник