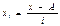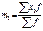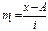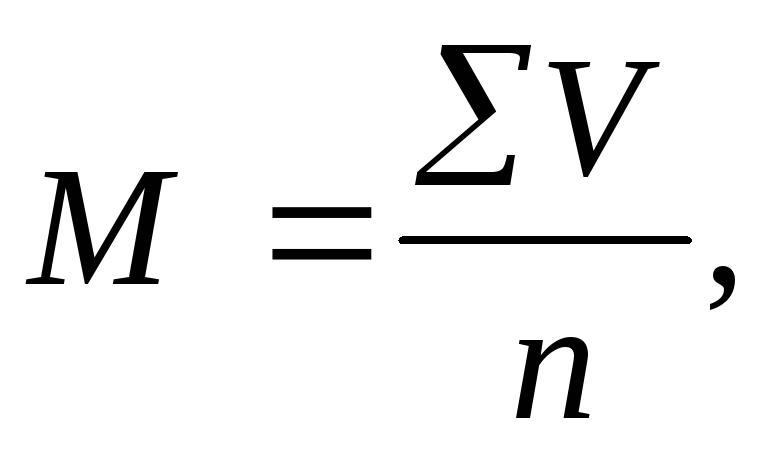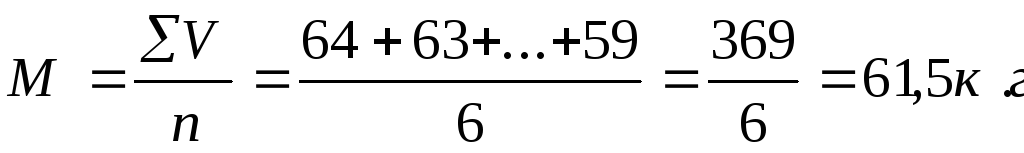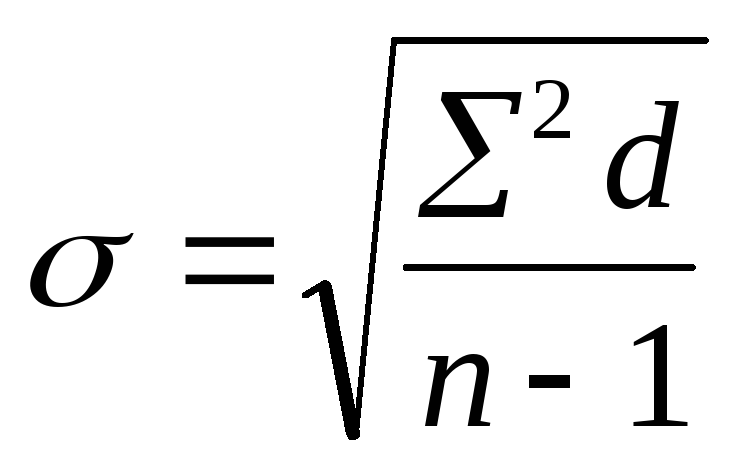- Расчет средних показателей способом моментов.
- Вычисление средней арифметической по способу моментов
- 5.2. Вычисление средней из вариационного ряда «способом моментов»
- Расчет средней арифметической величины способом моментов
- Основные свойства средней величины:
- Виды средних величин
- Вычисление средней арифметической , простой и взвешенной
- Вычисление средней арифметической по способу моментов
Расчет средних показателей способом моментов.



Вычисление средней арифметической часто сопряжено с большими затратами времени и труда. Однако в ряде случаев процедуру расчетов средней можно упростить и облегчить, если воспользоваться ее свойствами:
1. если все индивидуальные значения признака (все вварианты) уменьшить в i раз, то среднее значение нового признака соответственно уменьшится или увеличитсяв i раз.
2. Если вес варианты осредняемого признака уменьшить на число А, то средняя арифметическая соответственно увеличится на это же число А.
3. Если веса всех осредняемых вариантов уменьшить или увеличить в К раз, то средняя арифметическая не изменится.
В качестве весов средней вместо абсолютных показателей можно использовать удельные веса в общем итоге (доли или проценты). Тем самым достигается упрощение расчетов средней.
Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот. Наибольшее упрощение достигается, когда в качестве А выбирается значение одного из центральных вариантов, обладающего наибольшей частотой, в качестве i – величина интервала (для рядов с одинаковыми интервалами). Величина А называется началом отчета, поэтому такой метод вычисления средней называется “способом отчета от условного нуля” или “способом моментов”.
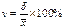 |
Допустим, что все варианты X сначала уменьшены на одно и то же чило А, а затем уменьшены в i раз. Получим новый вариационный ряд распределения новых вариантов x.
Тогда новые варианты будут выражаться ,
а их новая средняя арифметическая
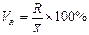 |
m 1 – момент первого порядка- формулой и будет равна средней из первоначальных вариантов, уменьшенной сначала на А, а затем в i раз, т.е.
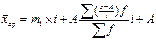 |
Для получения действительной средней надо момент первого порядка m 1 умножить на i и прибавить А.
Данный способ вычисления средней арифметической из вариционного ряда называют «способом моментов». Применяется этот способ в рядах с равными интервалами.
Источник
Вычисление средней арифметической по способу моментов
При большом числе наблюдений или при большом числовом значении вариант применяют
упрощенный способ вычисления средней арифметической- способ моментов.
где М — средняя арифметическая; А — условная средняя; i — интервал между группами вариант;
S — знак суммирования.; а- условное отклонение каждой варианты от условной средней;
р — частота встречаемости вариант; n — число наблюдений.
Пример вычисления средней арифметической по способу моментов (средней массы тела
юношей в возрасте 18 лет)
| V(n в кг) | Р | а (V-А) | а . Р |
| +2 | +4 | ||
| +1 | +3 | ||
| Мо=62 | |||
| -1 | -6 | ||
| -2 | -8 | ||
| -3 | -3 | ||
| п = 25 | Sар = — 10кг |
Этапы расчета средней по способу моментов:
1) за условную среднюю А рекомендуется принять Моду или Медиану, например А = 62кг, так как 62 кг было у 9 юношей из 25;
2) определяем «а» — условное отклонение варианты от условной средней, для этого из каждой варианты вычитаем условную среднюю: а = V — А, ( например, а = 64 — 62 = +2 и т.д.).
3) умножаем условное отклонение «а» на частоту «р» каждой варианты и получаем произведение а р;
4) находим сумму Sа . р = — 10кг
5) рассчитываем среднюю арифметическую по способу моментов:
М = А + i SаР = 62 — 1×0,4 = 61,6кг
Таким образом, можно сделать вывод, что в изучаемой нами группе юношей средняя масса тела
Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого
она была вычислена. На ее типичность (достоверность) влияет однородность рассматриваемого
материала и колеблемость ряда.
Пример: даны два одинаковых по числу наблюдений вариационных ряда, в которых
представлены данные измерений окружности головы детей в возрасте от 1 года до 2-х лет
| Ряд 1 | Ряд 2 | |
| Окружность головы(в см) Частота | 41, 45, 46, 47, 48 7, 8, 25, 6, 2 | 42, 43, 44, 45, 46, 47, 48, 49, 50 1, 2, 4, 6, 14, 10, 3, 0, 2 |
Имея одинаковое число наблюдений и одинаковые средние арифметические (М= 46 см), ряды
имеют различия в распределении внутри. Так варианты первого ряда отклоняются в целом от
средней арифметической с меньшим значением, чем варианты второго ряда, что дает
возможность предположить, что средняя арифметическая (46 см) более типична для первого
ряда, чем для второго.
В статистике для характеристики разнообразия вариационного ряда употребляют среднее
квадратическое отклонение (s)
Существует два способа расчета среднего квадратического отклонения: среднеарифметический
способ и способ моментов. При среднеарифметическом способе расчета применяют формулу:
где d истинное отклонение каждой варианты от истиной средней М. Формула используется при
Источник
5.2. Вычисление средней из вариационного ряда «способом моментов»
«Способ моментов» применяется в рядах с равными интервалами на основе свойств средней арифметической. Средняя арифметическая исчисляется по формуле
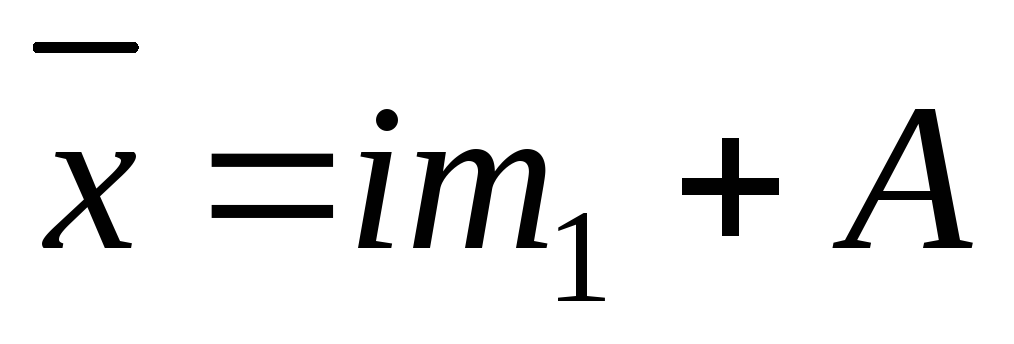
где i – размер интервала;
m1 – момент первого порядка (средняя арифметическая из новых упрощенных вариант 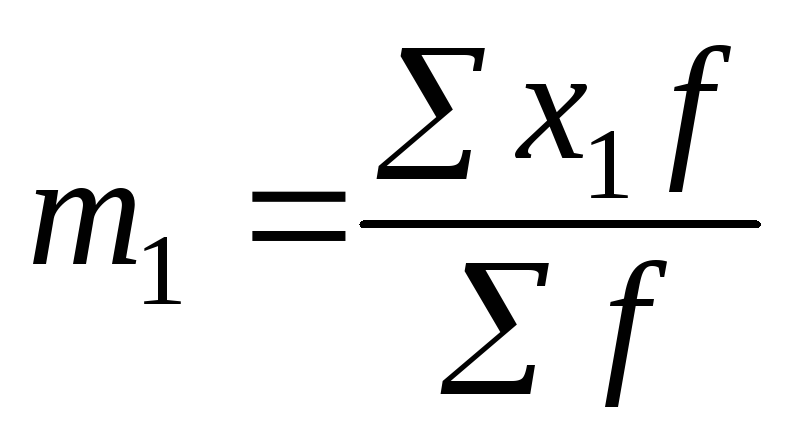
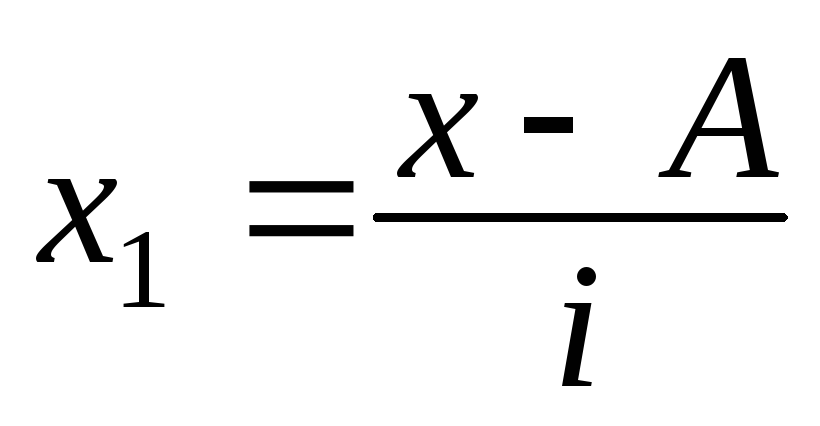
А– постоянное число (лучше всего взять его равным варианте, у которой наибольшая частота).
Определим среднее значение признака «способом моментов» на следующем примере.
Пример 5. Имеются следующие данные о распределении магазинов облпотребсоюза по торговой площади (табл. 14).
Группировка магазинов по торговой площади, м 2 (х)
Удельный вес магазинов, % ( f )
Следует определить среднюю площадь магазинов, применив «способ моментов».
Данные распределения магазинов по торговой площади представлены в виде интервального ряда распределения с равными интервалами (i = 20 м 2 ), следовательно, расчет средней площади магазина можно провести по формуле 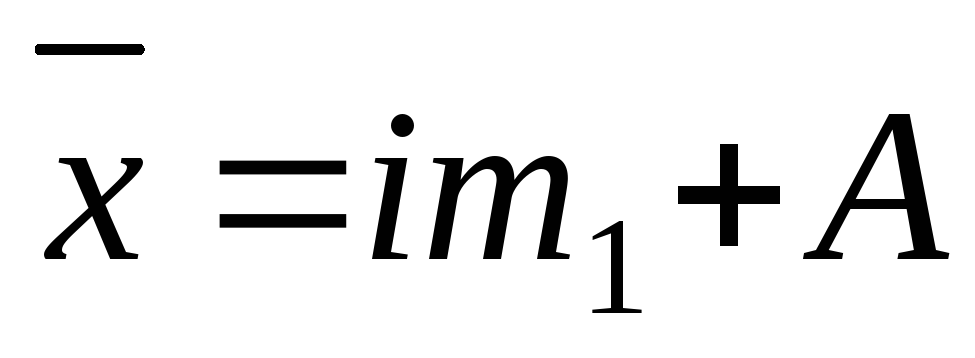
Первый и последний интервалы даны открытыми, т. е. не имеют границ нижней и верхней соответственно. Для определения среднего значения в них границы интервалов следует закрыть. Для первой группы с размером площади до 40 м 2 условно считаем, что интервал также равен 20 м 2 , затем вычитаем 20 м 2 из 40 м 2 и находим условную нижнюю границу первого интервала (20 – 40). Условную верхнюю границу последнего интервала определяем аналогично (100 – 120).
Расчеты следует проводить в табл. 15.
Группировка мага- зинов по торговой площади, м 2 (х)
Источник
Расчет средней арифметической величины способом моментов



Этот способ расчета средней арифметической величины основан на использовании ее математических свойств. Среднюю арифметическую величину вычисляют по формуле
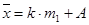
где 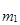
k – величина равного интервала или любое постоянное число, отличное от нуля;
А – любое постоянное число.
Момент 1-го порядка вычисляют по формуле
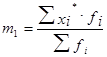
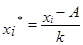
Пример 3. По исходным данным примера 2 вычислить средний размер премии одного работника способом моментов.
Решение. Пусть А = 6 000 и k = 500. Расчеты представлены в таблице:
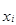 | 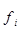 | 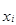 | 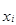 – 6000 – 6000 | 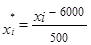 | 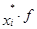 |
| 3 000–5 000 | 4 000 | – 2 000 | – 4 | – 16 | |
| 5 000– 7000 | 6 000 | ||||
| 7 000–10 000 | 8 500 | 2 500 | |||
| 10 000–15 000 | 12 500 | 6 500 | |||
| Итого |
Вычислим момент первого порядка
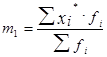
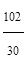
Средний размер заработной платы одного работника составил
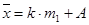
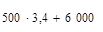
Источник
Основные свойства средней величины:
1.имеется абстрактный характер так как является обобщающей величиной, в ней стираются
2.занимает срединное положение в ряду (в строго симметричном ряду)
3.сумма отклонений всех вариант от средней величины равна нулю. Данное свойство средней
величины используется для проверки правильности расчета средней величины.
Виды средних величин
1. Мода (Мо) — варианта, наиболее часто встречающая и в вариационном ряду.
2. Медиана (Ме) — варианта занимающая в вариационном ряду срединное
положение, т.е., центральная варианта, делящая вариационный ряд на две
3. Средняя арифметическая:
а).Средняя арифметическая простая
б).Средняя арифметическая взвешенная
в). Средняя арифметическая, вычисленная по способу моментов.
Вычисление средней арифметической , простой и взвешенной
В случаях, когда мы имеем простой вариационный ряд, в котором каждой варианте
соответствует частота (Р) равная 1, вычисляется средняя арифметическая простая по
формуле:
где М средняя арифметическая - знак суммирования V — варианта, n — число наблюдений
Таким образом, средняя арифметическая простая равна сумме всех вариант, деленной на число
Пример: Определение средней массы тела юношей в возрасте 18 лет (в кг)
Однако чаще всего приходится вычислять среднюю арифметическую взвешенную, которая
получается из взвешенных рядов, где каждая варианта
или, как говорят, имеет различный вес.
Средняя арифметическая взвешенная вычисляется по формуле:
n где М средняя арифметическая - знак суммирования , V — варианта,
Р -частота встречаемости, n — число наблюдений
Таким образом, средняя арифметическая взвешенная равна сумме произведений вариант на их
частоты, деленной на число всех наблюдений.
Пример: определение средней массы тела юношей в возрасте 18 лет (в кг.)

Вычисление средней арифметической по способу моментов
При большом числе наблюдений или при большом числовом значении вариант применяют
упрощенный способ вычисления средней арифметической- способ моментов.
где М — средняя арифметическая; А — условная средняя; i — интервал между группами вариант;
— знак суммирования.; а- условное отклонение каждой варианты от условной средней;
р — частота встречаемости вариант; n — число наблюдений.
Пример вычисления средней арифметической по способу моментов (средней массы тела
юношей в возрасте 18 лет)
Этапы расчета средней по способу моментов:
1) за условную среднюю А рекомендуется принять Моду или Медиану, например А = 62кг, так как 62 кг было у 9 юношей из 25;
2) определяем «а» — условное отклонение варианты от условной средней, для этого из каждой варианты вычитаем условную среднюю: а = V — А, ( например, а = 64 — 62 = +2 и т.д.).
3) умножаем условное отклонение «а» на частоту «р» каждой варианты и получаем произведение а р;
4) находим сумму а . р = — 10кг
5) рассчитываем среднюю арифметическую по способу моментов:
М = А + i аР = 62 — 10,4 = 61,6кг
Таким образом, можно сделать вывод, что в изучаемой нами группе юношей средняя масса тела
Средняя арифметическая сама по себе ничего не говорит о том вариационном ряде, из которого
она была вычислена. На ее типичность (достоверность) влияет однородность рассматриваемого
материала и колеблемость ряда.
Пример: даны два одинаковых по числу наблюдений вариационных ряда, в которых
представлены данные измерений окружности головы детей в возрасте от 1 года до 2-х лет
Окружность головы(в см)
42, 43, 44, 45, 46, 47, 48, 49, 50
1, 2, 4, 6, 14, 10, 3, 0, 2
Имея одинаковое число наблюдений и одинаковые средние арифметические (М= 46 см), ряды
имеют различия в распределении внутри. Так варианты первого ряда отклоняются в целом от
средней арифметической с меньшим значением, чем варианты второго ряда, что дает
возможность предположить, что средняя арифметическая (46 см) более типична для первого
ряда, чем для второго.
В статистике для характеристики разнообразия вариационного ряда употребляют среднее
Существует два способа расчета среднего квадратического отклонения: среднеарифметический
способ и способ моментов. При среднеарифметическом способе расчета применяют формулу:
где d истинное отклонение каждой варианты от истиной средней М. Формула используется при
небольшом числе наблюдений (п 30)
Формула для определения по способу моментов:
где а — условное отклонение варианты от условной средней 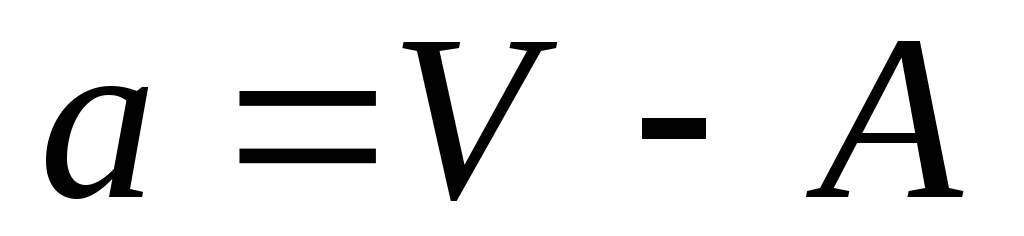
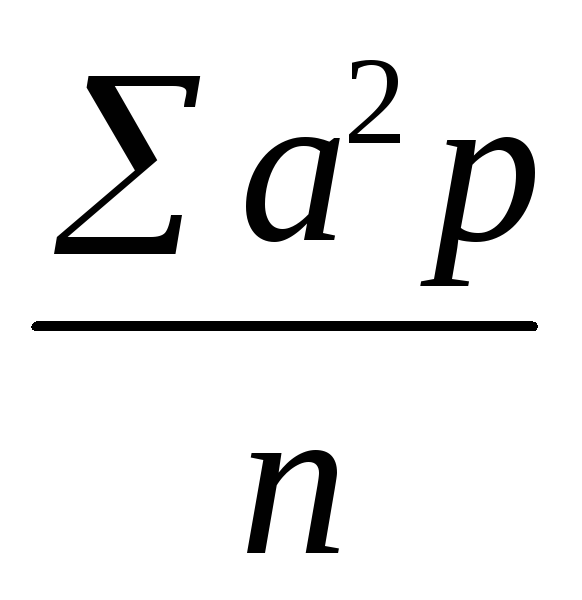
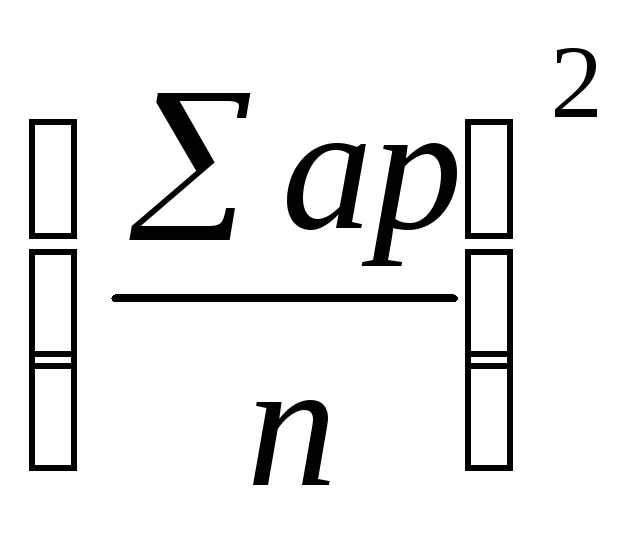
Теоретически и практически доказано, что если при большом числе наблюдений к средней
арифметической прибавить и отнять от нее 1(М1), то в пределах полученных величин
будет находится 68,3% всех вариант вариационного ряда. Если к средней арифметической
прибавить и отнять 2(М2), то в пределах полученных величин будет находиться 95,5%
всех вариант. М 3включает в себя 99,7% всех вариант вариационного ряда.
Исходя из этого положения можно проверить типичность средней арифметической для
вариационного ряда, из которого она была вычислена. Для этого надо к средней
арифметической прибавить и от нее отнять утроенную (М3). Если в полученные пределы
данный вариационный ряд укладывается, то средняя арифметическая типична, т.е. она
выражает основную закономерность ряда и ей можно пользоваться.
Указанное положение широко применяется при выработке различных стандартов (одежды,
обуви, школьной мебели и т.д).
Степень разнообразия признака в вариационном ряду можно оценить покоэффициенту
вариации(отношение среднего квадратического отклонения к средней арифметической,
умноженное на 100% )
При Сvменее 10% отмечается слабое разнообразие, при Сv10-20% — среднее, а при более 20% —
сильное разнообразие признака.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник