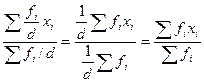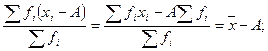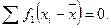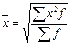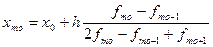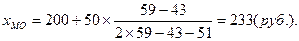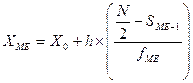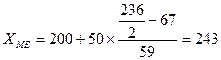Расчет средней арифметической взвешенной арифметическим способом

Средняя арифметическая, способы расчета

Если данные представлены в виде ряда распределения, то вопрос о выборе формы средней решается однозначно — средняя ариф­метическая. Этот вывод можно сделать, если вспомнить о том что ряд распределения есть не что иное как распределение значе­ний варьирующего признака по частоте их появлений в совокуп­ности.

Ряды распределения довольно часто встречаются в статистиче­ской практике. При этом варианта может быть задана в виде ин­тервалов, если признак непрерывный, или в виде индивидуаль­ных значений, если ряд дискретный. Для дискретных рядов рас­чет осуществляется по вышеприведенной формуле средней арифметической взвешенной. Для интервального ряда распреде­ления задача расчета средней величины решается следующим об­разом. Предполагаем, что в пределах интервала значения призна­ков располагаются равномерно, поэтому середина интервала бу­дет величиной, характеризующей весь интервал, то есть наиболее типичным для него значением. Данное предположение не всегда выполняется поэтому, чем меньше величина интервала, тем точ­нее его середина будет характеризовать весь интервал. Далее ис­пользуется обычная формула средней, только значения варианты будут приравниваться к середине соответствующего интервала. Расчет средней по непрерывному признаку (представленному в виде интервалов) был рассмотрен в примере 2.

В том случае, если ряд распределения имеет равные интервалы, расчет средней может быть существенно упрощен. Упрощенные способы расчета средней арифметической базируются на знании ее свойств.

Свойства средней арифметической:

— если все веса (f) увеличить или уменьшить в одинаковое число раз (d), то величина средней не изменится:

— если каждую варианту (х) увеличить или уменьшить на одну и ту же величину, то средняя увеличится или уменьшится на эту же величин:

— если каждую варианту (х) увеличить или уменьшить в одно и то же число раз (h), то средняя увеличится или уменьшится в то же число раз.

— сумма отклонений вариант от средней, взвешенных их частотами равна нулю:

Перечисленные свойства средней арифметической используются при расчете средней способом моментов или способом отсчета от условного начала (0). При использовании этого способа последо­вательно осуществляются следующие операции:

— определяются срединные значения интервалов как полу­сумма начала и конца интервалов;

— варианта (серединное значение интервала) с наибольшей частотой принимается за условное начало отсчета (А);

— рассчитывается момент 1 -го порядка:

где

i — величина интервала.

Средняя рассчитывается по формуле:

Пример расчета средней арифметической способом моментов.

Имеются следующие данные о продаже трехкомнатных квартир агентством недвижимости (табл. 6):

Стоимость квартир, тыс. руб.	Число квартир в группе, f	x	x’	x’f
250—300	-2	-300
300—350	-1	-200
350—400
400—450
450—500
500—550	3
550—600	4
600—650	ПО
Итого

Определите среднюю стоимость квартиры.

При использовании способа моментов удобнее всего результаты расчетов заносить в таблицу, для этого заранее в таблице резервируется три расчетных графы.

На основании данных таблицы рассчитываем момент 1-го порядка: итог по 5 столбцу делим на итог по 2 столбцу.

(тыс. руб.)

Средняя стоимость квартир выставленных на продажу составляет 404 тыс, руб.

Наряду со средней арифметической и средней гармонической, к другим степенным средним относится средняя геометрическая. В статистике она используется для осреднения темпов роста, коэф­фициентов динамики:

Средняя квадратическая используется при расчете показателей вариации, в частности — среднеквадратического отклонения, при исчислении средних ошибок выборки:

,

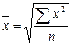
Структурные средние

Модаи медиана определяются структурой распределения. Они позволяют определить среднюю величину без производства вы­числений, визуально. Их используют в том случае, когда расчет степенных средних невозможен или нецелесообразен.

В дискретном ряду распределения мода определяется визуально. Например, распределение семей по числу /детей:

4 и более детей 2

В данном ряду распределения мода равна 2, то есть в данной со­вокупности наиболее часто встречаются семьи с двумя детьми. Очень удобно использовать этот показатель для характеристики наиболее часто встречаемого значения признака, определяемого по большой совокупности. Например, наиболее часто спраши­ваемый размер обуви, размер одежды и т.д.

В интервальном ряду распределения, когда наиболее часто встречаемое значение признака задано в виде интервала, а мода должна отражать конкретное значение признака, используется следующая формула расчета:

х₀ — верхняя граница модального интервала;

h — величина интервала:

— частоты модального, предмодального и послемодальнего интервалов.

В качестве модального берется интервал с наибольшей частотой.

Пример расчета моды по интервальному ряду распределения. Имеются следующий ряд распределения по среднедушевому доходу населения (табл. 7):

Интервалы по среднедушевому доходу, руб.	Число семей, fi	Накопленные частоты, Si
До 100
100—150
150—200
200—250
250—300
300—350
350—400
450—500
550—600
Итого	X

По данным таблицы, наиболее часто встречаются семьи со среднедушевым доходом от 200 до 250, то есть наибольшей частоте (59) соответствует интервал 200—250. Данный интервал и будет модальным. Расчет по формуле позволяет получить более точное значение.

В данной совокупности наиболее часто встречаются семьи со среднедушевым доходом 233 рубля.

Медиана— варианта, которая делит ранжированный ряд рас­пределения на две равные части. По обе стороны от медианы на­ходится одинаковое число единиц совокупности.

В дискретном ряду распределения медиана определяется визуально. Ряд признаков ранжируется, то есть значения признака упорядочиваются по возрастанию или убыванию. Варианта, ко­торая делит упорядоченный ряд пополам, будет медианой. Медиана в интервальном ряду распределения определяется по формуле:

где X_ME — верхняя граница медианного интервала;

X₀ — величина интервала;

h — общая численность;

S_ме-1 — накопленные частоты предмедианного интервала:

f_ме — частота медианного интервала.

В качестве медианного берется интервал, в котором находится единица совокупности, которая делит упорядоченный по значе­нию признака ряд пополам. Для того чтобы определить медиан­ный интервал, рассчитывают накопленные частоты. Последняя накопленная частота показывает общее количество единиц сово­купности.

Пример расчета медианы (по данным табл. 7). Последняя накопленная частота — 236. Медиан­ный интервал должен содержать единицу совокупности, которая делит всю совокупность из 236 се­мей пополам (236/2 = 118). Значит, в качестве медианного в расчете будем брать интервал 200—250. так как среднедушевой доход до 200 руб. имеют 67 семей из данной совокупности, то есть менее по­ловины совокупности. А интервалу 200—250 соответствует накопленная частота 126, значит, именно в этом интервале находится значение признака, которое разделит совокупность пополам, то есть 118 семей будут иметь среднедушевой доход ниже медианного и 118 семей — выше медианного. Произ­ведем расчет медианы по формуле для интервального ряда:

В изучаемой совокупности половина семей имеет доход ниже 243 руб. на человека.

1. Различают три вида статистических величин: абсолютные, относительные, средние величины.

2. Относительные величины позволяют приводить данные в сопоставимый вид и производить сравнения, в то время как абсолютные величины характеризуют только абсолютные размеры явления и в сравнительных характеристиках используются редко.

3. В статистической практике используют следующие виды относительных величин:

4. Наиболее распространены в статистических расчетах средние величины, которые могут одним числом охарактеризовать всю совокупность при соблюдении условий расчета средней величины.

5. Различают два класса средних величин: степенные и структурные.

6. При расчете степенных средних для правильного выбора формулы расчета необходимо исходить из логической формулы расчета осредняемого показателя.

Задание 1.4.1.Имеются следующие данные по магазинам ООО «Триумф»:

Номер магазина	Процент выполнения плана	Товарооборот, тыс. руб.
№ 1 №2 №3

Определите средний процент выполнения плана.

Задание 1.4.2.Имеются следующие данные по группе предприятий:

№ предприятия

Рентабельность, %

Реализованная продукция, тыс.руб.

Определите среднюю рентабельность по группе предприятий.

Библиографический список

Общая теория статистики: Учебник / Под ред. чл.-корр. РАН И.И.Елисеевой.— М.: Финансы и атистика, 2000.—С. 42—57.

Практикум по теории статистики: Учеб. пособие / Под ред. проф. Р.А.Шмойловой.— М.: Финан-

и статистика, 1999.—С. 97—109.

Статистика: Курс лекций / Под ред. Ионина В.Г.— Новосибирск: Издательство НГАЭиУ, 1996.— 59—84.

Теория статистики: Учебник / Под ред. проф. Р.А. Шмойловой.— М.. 1996.

Лунеев В.В. Юридическая статистика: Учебник.— М.: Юристъ, 1999.— С. 247—272. СавюкЛ.К. Правовая статистика: Учебник.— М.: Юристъ, 1999.— С 396—412.

Источник

Средняя арифметическая

Самым распространенным видом средней является средняя арифметическая.

Средняя арифметическая простая

Простая среднеарифметическая величина представляет собой среднее слагаемое, при определении которого общий объем данного признака в совокупности данных поровну распределяется между всеми единицами, входящими в данную совокупность. Так, среднегодовая выработка продукции на одного работающего — это такая величина объема продукции, которая приходилась бы на каждого работника, если бы весь объем выпущенной продукции в одинаковой степени распределялся между всеми сотрудниками организации. Среднеарифметическая простая величина исчисляется по формуле:

Простая средняя арифметическая — Равна отношению суммы индивидуальных значений признака к количеству признаков в совокупности

Пример 1 . Бригада из 6 рабочих получает в месяц 3 3,2 3,3 3,5 3,8 3,1 тыс.руб.

Найти среднюю заработную плату
Решение: (3 + 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 тыс. руб.

Средняя арифметическая взвешенная

Если объем совокупности данных большой и представляет собой ряд распределения, то исчисляется взвешенная среднеарифметическая величина. Так определяют средневзвешенную цену за единицу продукции: общую стоимость продукции (сумму произведений ее количества на цену единицы продукции) делят на суммарное количество продукции.

Представим это в виде следующей формулы:

• — цена за единицу продукции;
• — количество (объем) продукции;

Взвешенная средняя арифметическая — равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков).Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.

Пример 2 . Найти среднюю заработную плату рабочих цеха за месяц

Заработная плата одного рабочего тыс.руб; X	Число рабочих F
3,2	20
3,3	35
3,4	14
4,0	6
Итого:	75

Средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:

Ответ: 3,35 тыс.руб.

Средняя арифметическая для интервального ряда

При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.

Средние, вычисляемые из интервальных рядов являются приближенными.

Пример 3. Определить средний возраст студентов вечернего отделения.

Возраст в годах !!х??	Число студентов	Среднее значение интервала	Произведение середины интервала (возраст) на число студентов
до 20	65	(18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20)	1235
20 — 22	125	(20 + 22) / 2 = 21	2625
22 — 26	190	(22 + 26) / 2 = 24	4560
26 — 30	80	(26 + 30) / 2 = 28	2240
30 и более	40	(30 + 34) / 2 = 32	1280
Итого	500	11940

Средние, вычисляемые из интервальных рядов являются приближенными. Степень их приближения зависит от того, в какой мере фактическое распределение единиц совокупности внутри интервала приближается к равномерному.

При расчете средних в качестве весов могут использоваться не только абсолютные, но и относительные величины (частость):

Средняя арифметическая обладает целым рядом свойств, которые более полно раскрывают ее сущность и упрощают расчет:

1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т.е.

2.Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:

3.Алгебраическая сумма отклонений индивидуальных значений признака от средней равна нулю:

4.Сумма квадратов отклонений вариантов от средней меньше, чем сумма квадратов отклонений от любой другой произвольной величины , т.е:

5. Если все варианты ряда уменьшить или увеличить на одно и то же число , то средняя уменьшится на это же число :

6.Если все варианты ряда уменьшить или увеличить в раз, то средняя также уменьшится или увеличится в раз:

7.Если все частоты (веса) увеличить или уменьшить в раз, то средняя арифметическая не изменится:

Источник