Расчёт трёхфазных цепей

Цепь трехфазного переменного тока состоит из трехфазного источника питания, трехфазного потребителя и проводников линии связи между ними.

Симметричный трехфазный источник питания можно представить в виде трех однофазных источников, работающих на одной частоте с одинаковым напряжением и имеющих временной угол сдвига фаз 120˚. Эти источники могут соединяться звездой или треугольником.

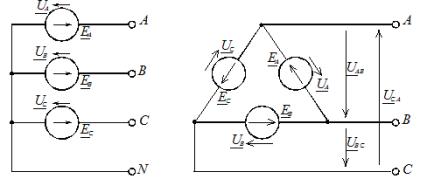
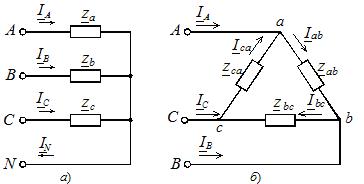
При соединении звездой условные начала фаз используют для подключения трех линейных проводников A, B, C, а концы фаз объединяют в одну точку, называемую нейтральной точкой источника питания (трехфазного генератора или трансформатора). К этой точке может подключаться нейтральный провод N. Схема соединения фаз источника питания звездой приведена на рисунке 1, а.

Рис. 1. Схемы соединения фаз источника питания: а – звездой; б – треугольником

Напряжение между линейным и нейтральным проводами называется фазным, а между линейными проводами – линейным (подробнее смотрите здесь — Линейное и фазное напряжение).

В комплексной форме записи выражения для фазных напряжений имеют вид:

Соответствующие им линейные напряжения при соединении звездой:

Здесь Uф – модуль фазного напряжения источника питания, а Uл – модуль линейного напряжения. В симметричной трёхфазной системе, при соединении фаз источника звездой, между этими напряжениями есть взаимосвязь:

При включении фаз треугольником фазные источники питания соединяют последовательно в замкнутый контур (рисунок 1, б).

Из точек объединения источников между собой выводятся три линейных провода A, B, C, идущие к нагрузке. Из рисунка 1, б видно, что выводы фазных источников подключены к линейным проводникам, а следовательно, при соединении фаз источника треугольником фазные напряжения равны линейным. Нейтральный провод в этом случае отсутствует.

К трехфазному источнику может подключаться нагрузка. По величине и характеру трёхфазная нагрузка бывает симметричной и несимметричной.

В случае симметричной нагрузки комплексные сопротивления всех трёх фаз одинаковы, а если эти сопротивления различны, то нагрузка несимметричная. Фазы нагрузки могут соединяться между собой звездой или треугольником (рисунок 2), независимо от схемы соединения источника.

Рис. 2. Схемы соединения фаз нагрузки

Соединение звездой может быть с нейтральным проводом (см. рисунок 2, а) и без него. Отсутствие нейтрального провода устраняет жёсткую привязку напряжения на нагрузке к напряжению источника питания, и в случае несимметричной нагрузки по фазам эти напряжения не равны между собой. Чтобы их отличить, условились в индексах буквенных обозначений напряжений и токов источника питания применять прописные буквы, а в параметрах, присущих нагрузке, – строчные.

Алгоритм анализа трёхфазной цепи зависит от схемы соединения нагрузки, исходных параметров и цели расчёта.

Для определения фазных напряжений при несимметричной нагрузке, соединённой звездой без нейтрального провода, используют метод двух узлов. В соответствии с этим методом расчёт начинают с определения напряжения UN между нейтральными точками источника питания и нагрузки, называемого напряжением смещения нейтрали:

где ya , yb , yc – полные проводимости соответствующих фаз нагрузки в комплексной форме

Напряжения на фазах несимметричной нагрузки находят из выражений:

В частном случае несимметрии нагрузки, когда при отсутствии нейтрального провода происходит короткое замыкание одной из фаз нагрузки, напряжение смещения нейтрали равно фазному напряжению источника питания той фазы, в которой произошло короткое замыкание.

Напряжение на замкнутой фазе нагрузки равно нулю, а на двух других оно численно равно линейному напряжению. Например, пусть произошло короткое замыкание в фазе В. Напряжение смещения нейтрали для этого случая UN = UB. Тогда фазные напряжения на нагрузке:

Фазные токи в нагрузке, они же и токи линейных проводов при любом характере нагрузки:

В задачах при проведении расчётов трёхфазных цепей рассматривают три варианта соединения трёхфазных потребителей звездой: соединение с нейтральным проводом при наличии потребителей в трёх фазах, соединение с нейтральным проводом при отсутствии потребителей в одной из фаз и соединение без нейтрального провода с коротким замыканием в одной из фаз нагрузки.

В первом и втором вариантах на фазах нагрузки находят соответствующие фазные напряжения источника питания и фазные токи в нагрузке определяются по приведенным выше формулам.

В третьем варианте напряжение на фазах нагрузки не равно фазному напряжению источника питания и определяется с помощью зависимостей

Токи, в двух незакороченных фазах, определяют по закону Ома, как частное от деления фазного напряжения на полное сопротивление соответствующей фазы. Ток в закороченной фазе определяют с помощью уравнения на основании первого закона Кирхгофа, составленного для нейтральной точки нагрузки.

Для рассмотренного выше примера с коротким замыканием фазы В:

При любом характере нагрузки трёхфазная активная и реактивная мощности равны соответственно сумме активных и реактивных мощностей отдельных фаз. Для определения этих мощностей фаз можно воспользоваться выражением

где U ф, I ф, – комплекс напряжения и сопряжённый комплекс тока на фазе нагрузки; Pф, Qф – активная и реактивная мощности в фазе нагрузки.

Трёхфазная активная мощность: P = P а + Pb + P с

Трёхфазная реактивная мощность: Q = Q а + Qb + Q с

Трёхфазная полная мощность:

При подключении потребителей треугольником схема приобретает вид, изображённый на рисунке 2, б. В этом режиме схема соединения фаз симметричного источника питания не играет роли.

На фазах нагрузки находят линейные напряжения источника питания. Фазные токи в нагрузке определяют с помощью закона Ома для участка цепи I ф = U ф/ z ф, где U ф – фазное напряжение на нагрузке (соответствующее линейное напряжение источника питания); z ф – полное сопротивление соответствующей фазы нагрузки.

Токи в линейных проводах определяют через фазные на основании первого закона Кирхгофа для каждого узла (точки a,b,c) схемы, изображённой на рисунке 2, б:

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Подписывайтесь на наш канал в Telegram!

Просто пройдите по ссылке и подключитесь к каналу.

Не пропустите обновления, подпишитесь на наши соцсети:

Источник

Расчет симметричной трехфазной цепи при различных способах соединения

Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах.

Расчет симметричных режимов работы трехфазных систем

Многофазный приемник и вообще многофазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если . В противном случае они являются несимметричными. Равенство модулей указанных сопротивлений не является достаточным условием симметрии цепи. Так, например трехфазный приемник на рис. 1,а является симметричным, а на рис. 1,б – нет даже при условии: .

Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется симметричным. В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол . Вследствие указанного расчет таких цепей проводится для одной – базовой – фазы, в качестве которой обычно принимают фазу А. При этом соответствующие величины в других фазах получают формальным добавлением к аргументу переменной фазы А фазового сдвига при сохранении неизменным ее модуля.

Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фаз можно записать

где определяется характером нагрузки .

Тогда на основании вышесказанного

;

Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:

При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:

Все треугольники заменяются эквивалентными звездами. Поскольку треугольники симметричны, то в соответствии с формулами преобразования «треугольник-звезда» .

Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.

Пусть, например, при заданном фазном напряжении необходимо определить линейные токи и в схеме на рис. 3, все сопротивления в которой известны.

В соответствии с указанной методикой выделим расчетную фазу А, которая представлена на рис. 4. Здесь , .

Тогда для тока можно записать

и соответственно .

Расчет несимметричных режимов работы трехфазных систем

Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее.

При заданных линейных напряжениях наиболее просто рассчитываются трехфазные цепи при соединении в треугольник. Пусть в схеме на рис. 2,а . Тогда при известных комплексах линейных напряжений в соответствии с законом Ома

; ; .

По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:

Обычно на практике известны не комплексы линейных напряжений, а их модули. В этом случае необходимо предварительное определение начальных фаз этих напряжений, что можно осуществить, например, графически. Для этого, приняв , по заданным модулям напряжений, строим треугольник (см. рис.5), из которого (путем замера) определяем значения углов a и b .

Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов:

При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет.

Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной нагрузке ей в общем случае будет соответствовать векторная диаграмма напряжений (см. рис. 6,б), на которой нейтральные точки источника и приемника занимают разные положения, т.е. .

Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением смещения нейтральной точки (обычно принимается, что ) или просто напряжением смещения нейтрали. Чем оно больше, тем сильнее несимметрия фазных напряжений на нагрузке, что наглядно иллюстрирует векторная диаграмма на рис. 6,б.

Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны:

Тогда для искомых токов можно записать:

Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид

(1)

При наличии нейтрального провода с нулевым сопротивлением , и из (1) . В случае отсутствия нейтрального провода . При симметричной нагрузке с учетом того, что , из (1) вытекает .

В качестве примера анализа несимметричного режима работы цепи с использованием соотношения (1) определим, какая из ламп в схеме на рис. 7 с прямым чередованием фаз источника будет гореть ярче, если .

Запишем выражения комплексных сопротивлений фаз нагрузки:

Тогда для напряжения смещения нейтрали будем иметь

Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника опускается)

Таким образом, наиболее ярко будет гореть лампочка в фазе С.

В заключение отметим, что если при соединении в звезду задаются линейные напряжения (что обычно имеет место на практике), то с учетом того, что сумма последних равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например, и . Тогда, поскольку при этом , соотношение (1) трансформируется в формулу

(2)

Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

Какой многофазный приемник является симметричным?
Какой режим работы трехфазной цепи называется симметричным?
В чем заключается специфика расчета симметричных режимов работы трехфазных цепей?
С помощью каких приемов трехфазная симметричная схема сводится к расчетной однофазной?
Что такое напряжение смещения нейтрали, как оно определяется?
Как можно определить комплексы линейных напряжений, если заданы их модули?
Что обеспечивает нейтральный провод с нулевым сопротивлением?
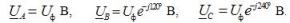
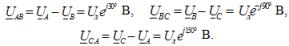
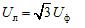
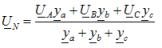
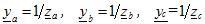
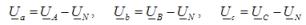
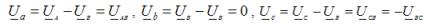
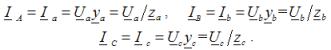
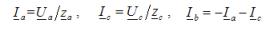
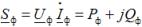
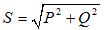
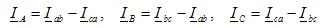
В цепи на рис. 6,а ; ; ; . Линейное напряжение равно 380 В.