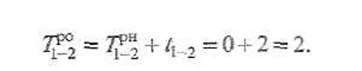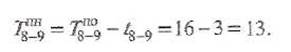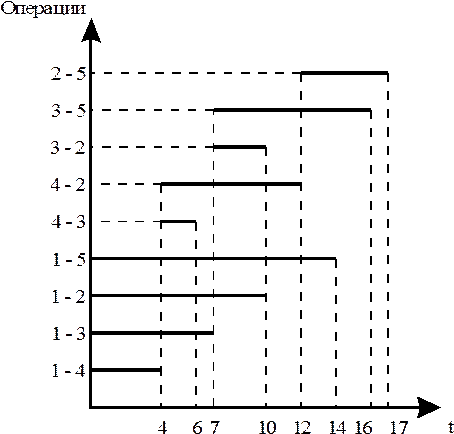РАСЧЁТ СЕТЕВЫХ ГРАФИКОВ ТАБЛИЧНЫМ (АНАЛИТИЧЕСКИМ) СПОСОБОМ
Основные закономерности и правила расчёта сетевых графиков табличным способом аналогичны рассмотренным ранее (формулы 1 — 9). При определении параметров сетевых моделей аналитическим способом расчёт выполняется в форме таблицы. Рассмотрим особенности расчёта сетевых моделей данным способом (см. табл. 1) на примере расчёта параметров сетевого графика, изображенного на рис. 6.
На начальном этапе необходимо описать исходную сетевую модель. При этом в первую графу таблицы заносятся шифры всех работ и зависимостей, начиная с работы, выходящей из первого события. Шифры работ должны быть включены в таблицу последовательно, произвольный порядок включения работ и зависимостей в таблицу недопустим. Во вторуюграфу таблицы вносятся продолжительности всех работ и зависимостей.
Расчёт сетевого графика начинается с определения значений ранних параметров работ. Раннее начало работы 1-2 равно нулю (формула 1), а её раннее окончание определяется по формуле 2
Раннее начало работ 2-3 и 2-4 (в соответствии с формулой 3) равно раннему окончанию работы 1-2, т.е.
Далее расчёт ранних параметров выполняется аналогично. Раннее начало работы 6-8 (в соответствии с формулой 4) равно максимальному значению из возможных ранних окончании предшествующихработ (в данном случае работ 3-6 и 5-6).
Максимальное значение раннего окончания работы 8-9, входящей в завершающее событие, равное 16, определяет продолжительность критического пути и, следовательно, общую продолжительность выполнения всех работ по исходной сетевой модели. Полученное значение раннего окончания завершающей работы 8-9 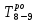
:
Позднее начало работы 8-9 в соответствии с формулой 5 определяется следующимобразом:

Далее расчёт поздних параметров выполняется аналогично, за исключением случаев,когда у работы имеется несколько последующих работ (например, у работы 4-5 имеется две последующих — 5-6 и 5-7). В этом случае, в соответствии с формулой 7, позднее окончание работы 4-5 равно минимальному значению поздних начал последующих работ 5-6 и 5-7.
В результате последовательного расчёта поздних параметров работ определяем значение позднего начала работы 1-2, которое оказалось равно нулю. Следовательно, можно сделать предварительное заключение о правильности выполненных расчётов.
Для нахождения положения критического пути необходимо определить значения общего и частного резервов времени для каждой работы и зависимости сетевого графика и занести их значения соответственно в 7 и 8 графы расчётной таблицы. Общий резерв времени работ, согласно формуле 8, определяется как разность позднего и раннего окончания либо как разность позднего и раннего начал соответствующих работ. Полезно определить значение общего резерва времени обоими способами, совпадение полученных значений может рассматриваться как дополнительная проверка. Например, для работы 4-7
Частный резерв времени работы, согласно формуле 9, определяется как разность значения раннего начала последующей работы и значения раннего окончания для данной работы. Например, для работы 4-7
Критический путь характеризуется равенством нулюрезервов времени. Сопоставлениепараметров сетевой модели, полученных секторным (раздел работы № 2) и табличным способами должно выявить их полную идентичность, наличие расхождений свидетельствует об ошибочности расчётов.
Задача 1Рассчитать сетевую модель секторным методом.
Задача 2
Рассчитать сетевую модель табличным методом.
| № начального события предшествующей работы | Код работы | Продолжительность | Ранние сроки | Поздние сроки | Резервы |
| Р.Н | Р.О | П.Н | П.О | R | r |
| — — | 1-2 1-3 | ||||
| 2-5 2-6 | |||||
| 3-4 3-7 | |||||
| 4-6 4-8 | |||||
| 5-9 | |||||
| 2,4 | 6-10 | ||||
| 7-8 7-12 | |||||
| 4,7 | 8-10 8-11 8-12 | ||||
| 9-13 | |||||
| 6,8 | 10-14 | ||||
| 11-14 11-15 | |||||
| 7,8 | 12-15 | ||||
| 13-16 | |||||
| 10,11 | 14-16 14-15 14-17 | ||||
| 11,12,14 | 15-18 | ||||
| 13,14 | 16-17 | ||||
| 14,16 | 17-18 | ||||
| 15,17 | 18-… |
Список использованной литературы
1 http://www.tstu.ru/book/elib/pdf/2010/alenicheva.pdf
2 http://oplib.ru/random/view/158446
3 http://www.studfiles.ru/preview/2899688/
4. Н.М. Губин, А.С. Добронравов, Б.С. Дорохов. Экономико-
математические методы и модели в планировании и управлении в от-
расли связи. — М.: Радио и связь, 1993.
5. М. Эддоус, Р. Стенсфилд. Методы принятия решений. — М.: Аудит,
ЮНИТИ, 1997.
Источник
Методы представления и расчета сетевых графиков



Методы расчета параметров сетевого графа делятся на две группы: аналитические и методы, основанные на теории статического моделирования. К первой группе относятся методы расчета по формулам, вычисления непосредственно на сетевом графе, табличный, матричный, графический и комбинированный.
Ко второй группе относятся методы, основанные на статическом моделировании. Их целесообразно применять при расчете стохастических сетей с очень большим разбросом возможных сроков выполнения работ.
Метод применяется в случаях, когда основные характеристики рассчитываются по формулам. На основании формул определяется резерв времени для каждого события. Критический путь проходит через события, имеющие нулевой резерв времени. Метод недостаточно наглядный, в особенности в случае развитой сети (большое количество событий и работ). Он хорош, в основном, для машинной обработки.
· Метод вычисления непосредственно на сетевом графе
Для определения параметров сети этим методом кружок, изображающий событие, делится на четыре сектора, в которые заносятся параметры сети. Метод рекомендуется применять в случаях, когда
– необходимо обеспечить наглядность;
– число событий и/или работ невелико, т.к. в этом случае достигается быстрая сходимость.
Метод заключается в последовательном занесении параметров сети в колонки таблицы по определенным правилам. Метод рекомендуется применять при формировании промежуточных отчетов, когда число событий и/или работ невелико.
Метод дает наглядность представления для небольших моделей с малым количеством вершин и сравнительно большим количеством работ.
Сетевой график может быть представлен в матричном виде. Строкам матрицы соответствуют вершины, инцидентные началам дуг, а столбцам – вершины, инцидентные концам дуг. Точка или весовой коэффициент проставляются в клетках матрицы, на пересечении i-й строки и j-го столбца, в том случае, если заданы связи между i-м и j-м событиями. Сток и исток обозначаются стрелками.
Этот метод применяется на начальной стадии проработки предметной области, при укрупненном описании модели во время постановки задачи.
· Графический метод (ленточный график – диаграмма Ганта)
Метод дает максимальную наглядность и позволяет быстро найти решение. В данном методе по горизонтальной оси откладывается время операций, а по вертикальной оси – сами операции (см. рис.). Метод применяется при неавтоматизированном и автоматизированном планировании, а также для представления результатов планирования.
Метод применяется на сложных сетях и в учебных целях. В этом случае решение сети проводится параллельно различными методами или сеть разрезается на удобные для анализа части так, чтобы последние решались по одному из перечисленных выше методов.
Алгоритм расчета сетевого графика с детерминированным временем выполнения операций
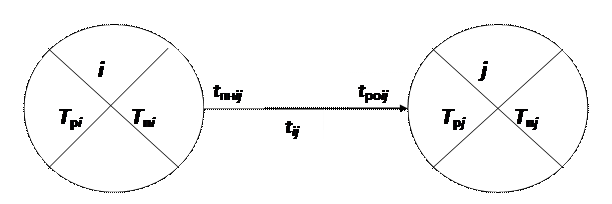
Примем следующие обозначения:
tij – время операции; i – номер предшествующего события; j – номер последующего события.
Tрi, Tрj– ранний срок наступления события, т.е. минимальный срок, необходимый для выполнения всех работ, предшествующих данному событию, tр.оij – ранний срок окончания операции i–j.
Tпi, Tпj – поздний срок наступления события, т.е. максимальный из допустимых моментов наступления данного события, при котором возможно соблюдение директивного (или расчетного) срока наступления завершающего события, tп.нij – поздний срок начала операции i–j.
Ri, Rj – резервы времени событий i, j, т.е. такой промежуток времени, на который может быть отсрочено наступление этих событий, без нарушения сроков завершения разработки в целом.
Rпij – полный резерв времени операций i–j, т.е. максимальное количество времени, на которое можно увеличить продолжительность данной операции, не изменяя при этом продолжительность критического пути.
Rсij – свободный резерв времени операции i–j, т.е. максимальное количество времени, на которое можно увеличить продолжительность операции или отсрочить ее начало, не изменяя при этом ранних сроков начала последующих работ, при условии, что начальное событие этой работы наступило в свой ранний срок.

Правила оформления и обозначения рассчитанных значений на графе и в таблицах при комбинированном методе расчета
Рассчитанные данные удобно заносить в таблицу и на граф в последовательности расчета.
Обозначение параметров на графе
Цифра в верхнем секторе каждой вершины – номер вершины i, j; в левом секторе – ранние сроки наступления события Tpj; в правом секторе – поздние сроки наступления события Tпj. Цифра в правом секторе отличается от цифры в левом на величину резерва времени события Rj. Цифра в середине дуги указывает время операции tij; у конца дуги – ранний срок окончания операции – tроij, у начала дуги – поздний срок начала операции – tпнij.
Задача согласования решается в три этапа.
I этап.Расчет ранних сроков наступления события Трj
Расчеты tроij и Трjведутся от начальной вершины сетевого графика к конечной. Ранний срок наступления первого события равен нулю, Тр1 = 0.
Ранний срок окончания операции tроiопределяется как сумма раннего срока наступления события i и времени операции i–j
Ранний срок наступления события Трi равен максимальному значению раннего срока окончания операций, подходящих к событию j,
II этап.Расчет поздних сроков наступления события Тпj.
Расчеты tпнij и Тпiведутся от конечной вершины сетевого графика к начальной. Для конечного события Трк = Тпк.
Поздний срок начала операции tпнij определяется как разность позднего срока наступления события j и времени операции i–j
Если от события отходит более одной операции, то Тпiравен минимальному значению позднего срока начала операций, отходящих от данного события i,
III этап.Расчет резервов времени.
Резерв времени события Ri определяется как разность между наиболее поздним и наиболее ранним сроками свершения этого события
Полный резерв времени операции Rпij определяется как разность между поздним сроком наступления события jи ранним сроком окончания операции i-j или разность между поздним сроком наступления события jи суммой раннего срока наступления события i и времени операции i-j
Свободный резерв времени операции Rсij определяется как разность между ранним сроком наступления события jи ранним сроком окончания операции i-j или разность между ранним сроком наступления события jи суммой раннего срока свершения события i и времени операции i-j
Источник