Расчет показателей динамики цепным способом

Статистика: Учебник / Под ред. Елисеевой.- М., 2006. С. 168-172

Оглавление

Показатели динамики (цепные и базисные)

Показатели динамики нашли широкое применения для формирования более наглядного представления о тенденции изменения уровней динамического ряда. Рост и снижение уровня ряда могут происходить либо равномерно, либо ускоренно, либо замедленно. Аналитические возможности показателей динамики раскрывает следующий фрагмент из учебника «Статистика»:

«Уровни временного ряда могут изменяться в самых разных, направлениях: они могут возрастать или убывать, повторять ранее достигнутый уровень. Интенсивность их изменения бывает различной. Уровни ряда могут изменяться быстрее или медленнее. Для характеристики развития явления во времени применяются следующие показатели:

• абсолютные приросты (_у);
• темпы роста (Т_р);
• темпы прироста (снижения) (Т_р);
• абсолютное ускорение или замедление ();
• относительное ускорение (Т_р).

Абсолютный прирост (абсолютное изменение) уровней ряда рассчи­тывается как разность двух уровней. Он показывает, на сколько единиц уровень одного периода больше или меньше уровня другого периода.

В зависимости от базы сравнения абсолютные приросты могут быть цепными и базисными:

Если каждый последующий уровень ряда динамики сравнивается со своим предыдущим уровнем, то прирост называется цепным. Если же в качестве базы сравнения выступает за ряд лет один и тот же период, то прирост называется базисным.

Один и тот же по величине абсолютный прирост может означать разную интенсивность изменения уровней (см. табл. 9.4).

Абсолютные приросты, тыс. шт.

Темпы роста, %

Темпы прироста, %

цепные

базисные

цепные

базисные

базисные

В нашем примере в 1996 и 1998 гг. абсолютное изменение объема продукции было одинаковым — 5 тыс. шт., но интенсивность рос­та объема произведенной продукции в эти годы была различной: в 1996 г. прирост в 5 тыс. ед. по сравнению с предыдущим годом составил 25%, а в 1998 г. по сравнению с предыдущим годом — лишь 14,3%. Аналогично один и тот же прирост в 10 тыс. ед. для 1997 и 1999 гг. означает разную интенсивность роста: в 1997 г. — прирост составил по сравнению с предыдущим годом, 40%, а в 1999 г. – 25%.

Интенсивность изменения уровней временного ряда характеризуется темпами роста и прироста.

Темп роста есть отношение двух уровней ряда. Как и абсолютные приросты, темпы роста могут рассчитываться как цепные и как базисные:

Если база сравнения по периодам меняется, то найденные темпы роста называются цепными. Если же база сравнения по периодам неизменна (y₀), то темпы роста называются базисными.

Темпы роста, выраженные в коэффициентах, принято называть коэффициентами роста:

В анализе используется один из этих показателей: либо темп роста, либо коэффициент роста, ибо экономическое их содержание одно и то же, но по-разному выражено: в % (Т_р) и в разах (К_р). Так по данным табл. 9.4 можно сделать вывод, что наибольшая интенсивность роста была достигнута в 1997 г., когда темп роста составил 140%, или в 1,4 раза превысил уровень предыдущего года.

Если цепные темпы роста характеризуют интенсивность изменения уровней от года к году (от месяца к месяцу), то базисные темпы роста фиксируют интенсивность роста, (снижения) за весь интервал времени между текущим и базисным уровнями. Так в примере базисный темп роста за весь период с 1996 по 1999 г. составил 250% (1995 г. взят за базу сравнения).

Темп прироста есть отношение абсолютного прироста к предыдущему уровню динамического ряда (цепной показатель) и к уровню, принятому за базу сравнения по динамическому ряду (базисный показатель):

По данным табл. 9.4, темп прироста для 1999 г. составит: цепной — 25% (·100) и базисный – 150% (·100), т.е. в 1999 г. объем продукции увеличился по сравнению с 1998 г. на 25%, а в целом за весь рассматриваемый период прирост составил 150%.

Между цепными и базисными показателями изменения уровней ряда существует следующая взаимосвязь:

• сумма цепных абсолютных приростов равна базисному приросту (см. табл. 9.4, где в итоговой строке накопленный прирост за 1996 — 1999 гг. – 30 тыс. шт. – совпадает с базисным абсолютным приростом для 1999 г.);
• произведение цепных коэффициентов роста равно базисному или равносильное этому деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентам роста. Так, по данным табл. 9.4, имеем:

, или 250% – базисный темп роста;

200/175=1,143, или 114,3% – цепной коэффициент роста для 1998 г. Взаимосвязь цепных и базисных темпов (коэффициентов) роста позволяет при анализе, если необходимо, переходить от цепных показателей к базисным и наоборот;

• темп прироста связан с темпом роста: (см. табл. 9.4, где темпы прироста меньше темпов роста на 100). Поэтому при анализе обычно приводится какой-то один из них: темп роста либо темп прироста. Зная цепные темпы прироста, можно определить базисный темп прироста. Для этого нужно от темпов прироста перейти к темпам (коэффициентам) роста и далее воспользоваться указанной выше взаимосвязью коэффициентов роста.

Так, например, изменение цен на потребительские товары и услуги за I квартал 2001 г. оказалось в Санкт-Петербурге следующим (см. гл. 9.5).

Изменение цен (в % к предыдущему месяцу)

В целом за I квартал прирост цен составит:

, т.е. в марте 2001 г. по сравнению с декабрем 2000 г. цены выросли на 7,4%.

Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за тот же промежуток времени:

или

Иными словами, абсолютное значение 1% прироста в данном периоде есть сотая часть достигнутого уровня в предыдущем периоде (см. табл. 9.4, последнюю графу). В связи с этим расчет абсолютного значения 1% прироста базисным методом не имеет смысла, ибо для каждого периода это будет одна и та же величина – сотая часть уровня базисного периода.

Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. Если они систематически возрастают, то ряд развивается с ускорением. Величина абсолютного ускорения определяется как т.е. по аналогии с цепным абсолютным приростом, но сравниваются между собой не уровни ряда, а их скорости. По табл. 9.4 в нашем примере ускорение имело место лишь в 1997 и в 1999 гг., когда =10-5=5 тыс. шт.

Если систематически растут цепные темпы роста, то ряд развивается с относительным ускорением. Относительное ускорение можно определить как разность следующих друг за другом темпов роста или прироста:

или

Полученная величина выражается в процентных пунктах (п.п.). По данным табл. 9.4, относительное ускорение имело место лишь в 1997 г.– 15 процентных пунктов по сравнению с предыдущим годом.

Относительное ускорение может быть измерено и с помощью коэффициента опережения.

Коэффициент опережения определяется как отношение последующего темпа роста к предыдущему:

В нашем примере коэффициент опережения для 1997 г. составил:

140/125=1,12, что означает, что в 1997 г. темп роста был в 1,12 раза больше, чем в 1996 г.

Коэффициенты опережения принято рассчитывать в сравнительном анализе нескольких рядов динамики. При параллельном изучении нескольких рядов динамики обычно их приводят к одному основанию путем расчета базисных темпов роста с одинаковой по времени базой сравнения для всех рядов. Это позволяет наглядно видеть, для какого ряда интенсивность изменения уровней наибольшая. Сравнивая далее наибольшие темпы роста с наименьшими, определяют коэффициенты опережения в развитии одного явления по отношению к другому (табл. 9.6).

Динамика доходов предприятия за 1-е полугодие 2004 г.(тыс. руб.)

Месяцы

Прибыль от реализации продукции

Прибыль от продажи прочих актов

Источник

Расчет показателей анализа динамики цепным способом

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 12

Тема 7: «Ряды динамики».

Цель занятия: получить навыки расчета показателей анализа динамики цепным и базисным способами.

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Понятие о рядах динамики и их виды

Ряд в статистике – это цифровые данные, показывающие измене­ние явления во времени или в пространстве.

Изменение социальных процессов и явлений во времени называют в статистике динамикой.

Ряд динами­ки –это ряд изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке.

Ряд динамики характеризуется двумя основными показателями ряда: показателем времени и уровень ряда.

Уровень в статистике — это размер (объем, величина) того или иного явления, достигнутый в определенный период или к определенному моменту. Различают начальный, средний и конечный уровни динамиче­ского ряда. Начальный уровень показывает величину первого, конечный — ве­личину последнего члена ряда.

Средний уровень (средняя хронологическая) представляет собой среднюю хронологическую вариационного ряда и исчисляется в за­висимости от того, является ли динамический ряд интервальным или моментным.

В интервальном ряду динамики (при равенстве интервалов) сред­ний уровень ряда исчисляется по простой средней арифметической. Он показывает общую характеристику уровня явления за весь на­блюдаемый период.

Уровень ряда, обычно обозначаемый символом «у», изначально выражен в абсолютных показателях, на ос­нове которых в процессе аналитической работы рассчитывается мно­жество производных обобщающих величин, относительных и средних.

Еще одна важная характеристика динамического ряда — его дли­на — время, прошедшее от начального до конечного наблюдения, или ко­личество таких наблюдений.

В зависимости от вида приводимых в динамических рядах обобщающих показателей их делят на ряды динамики абсолютных, относитель­ных и средних величин.

Рис. 1. Классификация рядов динамики.

Примером абсолютных рядов динамики являются данные о заре­гистрированных преступлениях в России за 1995-2003 гг., совершенных в состоянии опьянения (см. таблицу).

Количество преступлений, совершенных в состоянии опьянения

Годы	Произведено продукция, тыс. шт.	Абсолютное значении 1 % прироста, тыс. шт.
1995	1996	1997	1998	1999	2000	2001	2002	2003
Российская Федерация	650261	637012	508928	485160	488067	442656	408072	325580	315098
Центральный фед. округ	125905	125033	102776	99437	97613	90744	78628	60313	58311
Северо-Западный фед. округ	80040	79750	61292	60657	60947	53944	48858	33790	28926
Южный фед. округ	49085	46458	35898	32363	31001	28151	27023	22328	21017
Уральский фед. округ	81169	79232	55674	53731	58340	53454	50726	43504	42932
Приволжский фед. округ	144007	139467	115910	108890	111629	100366	97961	78612	78843
Сибирский фед. округ	111674	111932	93878	88451	87791	77787	69295	56487	56087
Дальневосточный фед. округ	45114	42779	33425	31422	30600	28236	26269	20417	28816

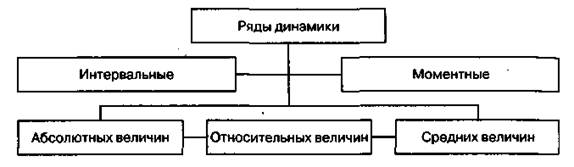
Принято различать моментные и интервальные ряды динамики.

Моментные рядыхарактеризуют уровни изменения юридически значимых явлений на определенные моменты времени (дату учета), например, на начало месяца, квартала, года или по состоянию на 1 ян­варя, 30 июня, 31 декабря и т.д. Типичные моментные ряды в судебной статистике — количество заключенных в колониях, следственных изоляторах или число судей, прокуроров, следователей, адвокатов в регионе, стране, взятые на какую-то дату за несколько лет. Период между датами в моментных ря­дах называется интервалом ряда. Он может быть годовым, кварталь­ным, месячным. Особенностью моментного ряда является то, что его показатели, раскрывая то или иное состояние, не могут суммироваться или укрупняться. Моментные ряды в аналитической работе правоохранительных органов используются сравнительно редко.

Интервальные рядыхарактеризуют величину изучаемого показате­ля, полученного за какой-то период времени (интервал). Поэтому месячные данные можно суммировать по кварталам, квар­тальные — по годам, годовые — по пятилетиям и т.д. В моментном ряду величина уровня ряда не зависит от размера интервала. И на начало ка­ждого месяца, и на начало каждого года общее число сотрудников про­куратуры в городе N может быть одним и тем же. В интервальном ряду величина уровня ряда существенно зависит от размера интервала. Чис­ло учтенных преступлений за год может быть (примерно) в 12 раз боль­ше, чем за любой из его месяцев. Иногда говорят, что моментный ряд учитывает состояние на какой-то момент, а интервальный ряд отражает деятельность (совершение преступлений, борьба с преступностью, установление юридических фактов и т.д.), сведения о которой характе­ризуются накопительностью.

Расчет показателей анализа динамики цепным способом

К основным показателям анализа динамики относят абсолютный при­рост(снижение), темп роста(снижения)темп прироста(снижения).

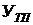
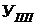
Абсолютный при­ростопределяется как разность между уровнем текущего периода и уровнем предшествующего периода динамического ряда

.

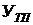
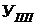
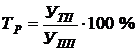
Темп ростаопределяется как процентное отношениеуровня текущего периода к уровню предшествующего периода динамического ряда

.

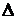
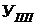
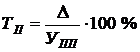
Темп прироста определяется как процентное отношениеабсолютного прироста текущего периода к уровню предшествующего периода динамического ряда

.

При цепном способе расчета показателей анализа динамики уровень текущего периода сравнивается с уровнем предшествующего периода (рис. 2).

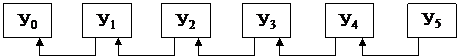Рис 2. Принцип расчета показателей цепным способом.

Дата добавления: 2018-06-01 ; просмотров: 311 ; Мы поможем в написании вашей работы!

Источник