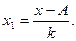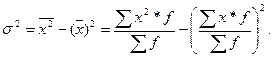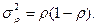Расчет дисперсии способом отсчета от условного нуля

Свойства дисперсии.

Поможем написать любую работу на аналогичную тему

1. Если из всех значений вариант вычесть какое-то постоянное число, то средний квадрат отклонений не изменится:

2. Если все значения вариант разделить на какое-то постоянное число, то средний квадрат отклонений уменьшиться в а раз:

3. Если средний квадрат отклонений от любой величины а – которая отличается от средней арифметической х, то он будет всегда больше среднего квадрата отклонений от средней арифметической: , но больше на определенную величину, а эта величина определена, как квадрат разности между средней и этой, условно взятой величиной:

используя 2-ое свойство дисперсии в математической статистике можно рассчитать дисперсию способом моментов. Средний квадрат отклонений от средней величины имеет свойства min, т.е. дисперсия от средней всегда меньше дисперсий исчисляемых от других величин. В этом случае, если а – постоянное число = 0, то, следовательно, средний квадрат отклонений будет определяться по формуле:

— ср. квадрат значений признака;

— квадрат среднего значения признака.

Значит, средний квадрат отклонений равен разности между средним квадратом значения признака и квадратом ср. значения признака.

Также способ моментов называется способом отсчета от условного нуля. Данный способ можно применять только в тех случаях, если в вариационных интервальных рядах интервалы одинаковы.

Используя 2-ое свойство дисперсии, разделив все варианты на величину интервала, получим формулу дисперсии:

где i – величина интервала для данной совокупности ;

Рассчитать все показатели вариации, доказать закон сложения дисперсии.

Расчет общей дисперсии

Источник

Моменты распределения

Дисперсия: способы ее расчета, виды дисперсии, правило сложения дисперсии.

Дисперсия обладает рядом математических свойств, позволяющих упростить ее расчет.

Первое свойство заключается в том, что если из всех вариант вычесть какое-то постоянное число, то дисперсия от этого не изменится. Оно позволяет рассчитывать дисперсию не по отклонениям вариант от средней (часто имеющей дробное значение), а по отклонениям от целого числа. Второе свойство позволяет все варианты разделить на какое-то постоянное число, например на значение интервала, и исчислить дисперсию уменьшенных вариант, а полученную величину умножить на квадрат этого числа.

, .

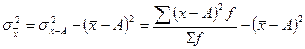
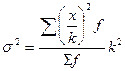
где: s 2 _x – дисперсия отклонений вариантов от средней арифметической;

– дисперсия отклонений вариантов от произвольной величины А.

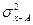
1. На этих свойствах основан расчет дисперсии способом отсчета от условного нуля или способ моментов, который заключается в нахождении вариант, уменьшенных на условно постоянную величину А и в k раз, где k – интервал, т.е. х₁=(х – А)/k, и последующем расчете дисперсии по формуле:

способ отсчета от условного нуля: ;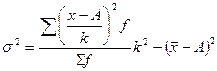

способ моментов: 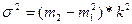, где

условный момент первого порядка: ;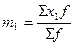

условный момент второго порядка: ,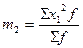

2. Дисперсия равна среднему квадрату значений признака за вычетом квадрата среднего значения признака:

Расчеты дисперсии различными способами дают одинаковые результаты, что позволяет исследователю выбрать наиболее эффективный способ.

В ряде случаев изучают не среднюю величину признака, а долю единиц, обладающих тем или иным признаком. Например, доля междугородных телефонных соединений (разговоров), предоставленных с ожиданием до 1 часа. Это примеры альтернативных вариаций, когда имеются лишь два взаимоисключающих варианта: наличие или отсутствие признака у данной единицы совокупности (1 наличие признака, 0 отсутствие). В таких случаях определяется дисперсия альтернативного признака. Пусть доля единиц, обладающих данным признаком, равна р, а доля единиц, не обладающих этим признаком, 1–р, тогда

Естественно, средняя постоянная величины р есть сама эта величина, а дисперсия равна:

Средняя и дисперсия это частные случаи более широкого понятия обобщающих характеристик любого распределения моментов.

Момент распределения – это средняя арифметическая тех или иных степеней отклонений вариантов х от некоторой постоянной величины А:

m_z = .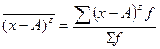

Порядок момента определяется величиной z, т.е. степенью, в которую возводится отклонение вариант. В зависимости от принятой величины А различают три вида моментов:

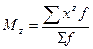
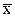
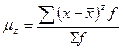
начальные (при А=0): ; центральные (при А=): ;

условные (при А≠0, А≠): .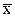

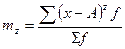
Начальный момент первого порядка представляет собой среднюю арифметическую: ;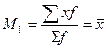

центральный момент второго порядка – дисперсию: 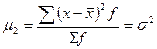. Центральный момент первого порядка m₁ всегда равен нулю (сумма отклонений вариант от средней равна нулю); центральный момент третьего порядка равен нулю в симметричном распределении.

Условные моменты самостоятельного значения не имеют, ими пользуются для упрощения вычисления центральных моментов: m₂ = m₂ – m 2 ₁; m₃ = m₃ – 3m₁ m₂ + 2m 3 ₁; m₄ = m₄ – 4m₃ m₁ + 6m₂ m 2 ₁ – 3 m 4 ₁.

Для исчисления условных моментов используется условная величина:

; ; ; ; где

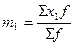
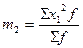
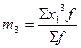
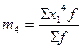
В этом случае центральные моменты корректируются на величину k z :

Наряду с изучением вариации признака по всей совокупности в целом часто возникает необходимость проследить количественные изменения признака по группам, на которые разбита вся совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных дисперсий: общей, межгрупповой, внутригрупповой и средней из внутригрупповых дисперсий.

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию:

.

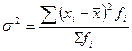
Межгрупповая дисперсияхарактеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки:

, где

— соответственно средние и численности по отдельным группам,

— средняя всей совокупности.

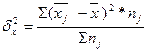
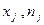
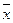
Внутригрупповая дисперсияотражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки:

, где

— варианты групп, — численность группы, — средняя группы

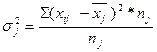
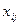
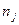
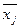
Средняя из внутригрупповых дисперсийопределяется по формуле:

.

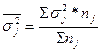
Общая дисперсия определяется как сумма средней из внутригрупповых дисперсий и межгрупповой дисперсии:

.

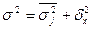
Данная сумма называется правилом сложения дисперсий.

Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием прочих факторов, и дисперсии, возникающей за счет группировочного признака.

На основании правила сложения дисперсий можно определить показатель тесноты связи между группировочным (факторным) и результирующим признаками. Он называется эмпирическим корреляционным отношением и рассчитывается как корень квадратный из отношения межгрупповой дисперсии к общей дисперсии:

.

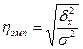
Отношения межгрупповой дисперсии к общей дисперсии называется эмпирическим коэффициентом детерминациии показывает долю группировочного признака в общей вариации:

.

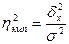
Источник