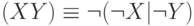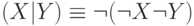Проверьте двумя способами будут ли эквивалентны следующие формулы

Проверьте двумя способами, будут ли эквивалентны следующие формулы

Проверьте двумя способами, будут ли эквивалентны следующие формулы: а) составлением таблиц истинности б) приведением формул к СДНФ или СКНФ с помощью эквивалентных преобразований

x сложение по модулю 2 (y->z)

(x сложение по модулю 2 y) -> (x сложение по модулю 2 z)

Проверить будут ли эквивалентны формулы, двумя способами
а) составление таблиц истинности б) путем эквивалентных преобразований.

Проверьте,будут ли эквивалентны следующие булевы функции
Проверьте,будут ли эквивалентны следующие булевы функции: x\rightarrow (y\mid z) , (x\rightarrow.

Проверить, используя СКНФ или СДНФ, будут ли эквивалентны следующие формулы
Приветствую :friends:. Будут ли эквивалентны следующие формулы — проверить это приведением.

Проверить двумя способами, будут ли эквиваленты указанные формулы
Добрый времени суток, помогите пожалуйста решить. Проверьте двумя способами , будут ли.

Проверить будут ли эквивалентны формулы
Добрый вечер, Ребят помогите пожалуйста решить 2 способом, 1 с помощью таблиц истинности вроде бы.

Проверить составлением таблиц истинности, будут ли эквивалентны указанные формулы
помогите пожалуйста, нужно: проверить составлением таблиц истинности, будут ли эквивалентны.

Доказать, что во всяком исчислении высказываний следующие формулы будут теоремами
Доказать,что во всяком исчислении высказываний,в котором правилом вывода является правило МР и в.

Упростить формулы логики двумя способами
Упростить формулы логики двумя способами: а) используя таблицы истинности б) с помощью.

Источник

6 задач по математической логике 2

Пример готовой контрольной работы по предмету: Прикладная математика

Содержание

Проверить двумя способами, будут ли эквивалентными следующие формулы:

а) составлением таблицы истинности;

б) приведение формул к СКНФ или СДНФ с помощью эквивалентных преобразований.

Решите логическое уравнение:

Является ли приведенная формула общезначимой? Противоречивой? Нейтральной? Не общезначимой? Выполнимой?

Формализуйте следующие предложения. Установите их истинность.

2. простое число и 3 простое число.

Для графика найдите матрицы смежности, инцидентности, сильных компонентов, маршрутов длины 2 и все маршруты длины

2. исходящие из вершины 1.

Логическая функция L(x,y) задана на множестве D= с помощью таблицы

Определите истинностные значения следующей формулы:

Выдержка из текста

Если формула F истинна при любых значениях своих аргументов в некоторой интерпретации, то она называется общезначимой.

Формула не является общезначимой.

Тождественно ложными (или противоречивыми) называются формулы, ложные в любой интерпретации.

Формула является не общезначимой.

Формула не является выполнимой.

Формула не является нейтральной.

Список использованной литературы

1. Гончарова Г.А., Молчалин А.А. «Элементы дискретной математики»: Учебное пособие. М.: ФОРУМ: ИНФРА-М, 2005. (Серия «профессиональное образование»).

2. Фомин Г.П. «Математические методы и модели в коммерческой деятельности»: Учебник. М.: Финансы и статистика, 2007.

3. Ерохина А.П. Байбакова Л.Н. Математика. Учебное пособие — Томск: ТМЦДО, 2004. — 257с.

4. Магазинников Л.И. Магазинников А.Л. ТМЦ ДО, 2003. — 191 с.

5. Иванова С А Павский В А Математика. Часть

1. Учебное пособие — Томск: ТМЦДО, 2006. — Ч.1. — 137 с.

Источник

Эквивалентность формул

Смотреть на youtube || на ИНТУИТ в качестве: низком | среднем | высоком

Одну и ту же функцию можно задать разными формулами. Поэтому возникает задача определения эквивалентности формул логики высказываний.

Две формулы эквивалентны, если они задают одну и ту же функцию. Как можно установить эквивалентность формул? Один из способов состоит в том, чтобы построить таблицу истинности. Если две формулы на всех возможных значениях переменных дают одно и то же значение , то они определяют одну и ту же функцию, следовательно, формулы эквивалентны.

Давайте установим эквивалентности для некоторых функций из таблицы 3 предыдущего урока.

Исключающее Или эквивалентно отрицанию эквивалентности:

Построим таблицы истинности для этих двух формул:

0	0	1	0	0
0	1	0	1	1
1	0	0	1	1
1	1	1	0	0

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Штрих Шеффера эквивалентен отрицанию конъюнкции:

Построим таблицы истинности для этих двух формул:

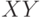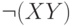0	0	0	1	1
0	1	0	1	1
1	0	0	1	1
1	1	1	0	0

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Операцию Штрих Шеффера называют антиконъюнкцией.

Стрелка Пирса эквивалентна отрицанию дизъюнкции:

Построим таблицы истинности для этих двух формул:

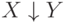0	0	0	1	1
0	1	1	0	0
1	0	1	0	0
1	1	1	0	0

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Операцию Стрелка Пирса называют антидизъюнкцией.

Импликация 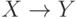эквивалентна дизъюнкции и отрицания :

Построим таблицы истинности для этих двух формул:

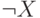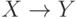0	0	1	1	1
0	1	1	1	1
1	0	0	0	0
1	1	0	1	1

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Эту эквивалентность , позволяющую избавиться от импликаций, часто используют при преобразовании формул.

Конъюнкция 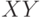эквивалентна отрицанию дизъюнкции отрицаний:

Построим таблицы истинности для этих двух формул:

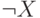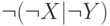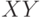0	0	1	1	1	0	0
0	1	1	0	1	0	0
1	0	0	1	1	0	0
1	1	0	0	0	1	1

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Дизъюнкция эквивалентна отрицанию конъюнкции отрицаний:

Построим таблицы истинности для этих двух формул:

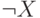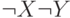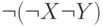0	0	1	1	1	0	0
0	1	1	0	0	1	1
1	0	0	1	0	1	1
1	1	0	0	0	1	1

Два последних столбца таблицы совпадают, — следовательно, формулы эквивалентны.

Почему на практике используется небольшое число функций?

Логических функций много, особенно функций многих переменных. Почему же мы знаем и оперируем небольшим числом функций? Связано это с тем, что одни функции можно выражать через другие, как мы видели на примерах. А можно ли любую функцию выразить через немногие, базисные функции? Ответ на этот вопрос положителен.

Каждую функцию от любого числа переменных можно представить в так называемой нормальной форме, в которой используются только три базисные функции – отрицание, конъюнкция и дизъюнкция.

Источник