Третий способ – сокращенный.
Практическое занятие № 4 «Логические рассуждения»
Определение: Пусть даны две формулы 
. Формула 
является логическим следованием формул 
, если, придавая значения переменным 
, от которых зависят все рассматриваемые формулы, всякий раз, когда истинны одновременно все формулы , истинна и формула .
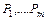
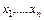
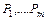
Для логического следования используется запись: 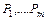├─ . Рассуждение будем записывать в виде схемы рассуждения: 
Три способа проверки правильности логического рассуждения:
I. Применить определение:
а) записать все посылки и заключения в виде формул логики высказываний;
б) составить конъюнкцию формализованных посылок 
;
в) проверить по таблице истинности, следует ли заключение из формулы .
II. Использовать Признак логического следования:
Формула логически следует из формулы 
тогда и только тогда, когда формула 
является тавтологией. Для проверки необходимо построить таблицу истинности для формулы , или преобразовать эту формулу с помощью равносильных преобразований к известной тавтологии.
III. Применить сокращенный способ проверки правильности логического рассуждения.
Рассуждение строится «методом от противного»:
Рассуждение является неправильным, если найдется набор значений переменных 
такой, что посылка ( ) =1, а заключение ( ) =0.
Сокращенный метод заключается в следующем.
Пусть требуется проверить правильность логического следования формулы из посылок .
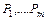
Предположим, что существует набор 
, при котором все посылки истинны, а заключение ложно, и попытаемся найти этот набор. Если такой набор будет обнаружен, то наше предположение оправдалось, и рассуждение является логически неправильным. Если в процессе поисков набора придем к противоречию, то наше предположение ошибочно, а рассуждение является логически правильным.
Если в параллелограмме диагонали взаимно перпендикулярны (А), то параллелограмм – ромб (B). В данном параллелограмме диагонали не взаимно перпендикулярны (отрицание А), следовательно, он не является ромбом (отрицание B)».
Составим схему логического рассуждения:
Первый способ проверки – по определению.Составляем конъюнкцию формализованных посылок: 
.
Проверим по таблице истинности:
 |  |  |  |  |  |
Так как на наборе (A=0, B=1) конъюнкция посылок истинна, а заключение ложно, то рассуждение не является логически правильным.
Второй способ, основанный на признаке логического следования.
Построим формулу и проверим, является ли она тавтологией.
.
Расставим приоритеты логических операций и построим таблицу истинности.
 |  |  |  |  |  |  |
Формула не является тавтологией, следовательно, данное логическое рассуждение не является логически правильным.
Третий способ – сокращенный.
Проверим сокращенным способом правильность логического рассуждения 
├─ 
.
Пусть существует набор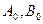 
при котором посылки истинны, а заключение ложно. Оформим это предположение в виде таблицы
| № | Истина | Ложь |
 |  | |
 |  | |
 |  |
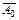Из строк 2,3 следует: , . Подставляем полученные значения в первую строку: . Таким образом, противоречий нет, следовательно, рассуждение ├─ не является логически правильным.
Если число представлено в виде несократимой дроби (A), то оно рациональное (B). Если число целое (C), то оно не является рациональным(отриц. В). Следовательно, если число целое(С), то оно не представлено в виде несократимой дроби(отриц. А)».
Решение: Составим схему логического рассуждения:
Первый способ проверки – по определению.Составляем конъюнкцию формализованных посылок: 
.
Проверим по таблице истинности:
| | |  |  |  | | |  | |
Так как нет наборов, где конъюнкция посылок истинна, а заключение ложно, то данное рассуждение является логически правильным.
Второй способ, основанный на признаке логического следования.
Построим формулу и проверим, является ли она тавтологией.
.
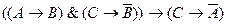
Расставим приоритеты логических операций и построим таблицу истинности.
| | | | | | | | | | |
Формула является тавтологией, следовательно, данное логическое рассуждение является правильным.
Источник
Проверить истинность соотношений двумя способами
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженbя ложны.
Обозначение: F = A v B.
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Обозначение: F = ¬ A.
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. То есть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Источник
