Простой способ шифрования чисел

10 популярных кодов и шифров

Авторизуйтесь

10 популярных кодов и шифров

Коды и шифры — не одно и то же: в коде каждое слово заменяется другим, в то время как в шифре заменяются все символы сообщения.

В данной статье мы рассмотрим наиболее популярные способы шифрования, а следующим шагом будет изучение основ криптографии.

Стандартные шифры

Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, А заменяется на Б, Б — на В, и т. д. Фраза «Уйрйшоьк Рспдсбннйту» — это «Типичный Программист».

Попробуйте расшифровать сообщение:

Сумели? Напишите в комментариях, что у вас получилось.

Шифр транспонирования

В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из hello world получается dlrow olleh. Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl.

Ещё можно использовать столбчатый шифр транспонирования, в котором каждый символ написан горизонтально с заданной шириной алфавита, а шифр создаётся из символов по вертикали. Пример:

Из этого способа мы получим шифр holewdlo lr. А вот столбчатая транспозиция, реализованная программно:

Азбука Морзе

В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов:
Чаще всего это шифрование передаётся световыми или звуковыми сигналами.

Сможете расшифровать сообщение, используя картинку?

Шифр Цезаря

Это не один шифр, а целых 26, использующих один принцип. Так, ROT1 — лишь один из вариантов шифра Цезаря. Получателю нужно просто сообщить, какой шаг использовался при шифровании: если ROT2, тогда А заменяется на В, Б на Г и т. д.

А здесь использован шифр Цезаря с шагом 5:

Моноалфавитная замена

Коды и шифры также делятся на подгруппы. Например, ROT1, азбука Морзе, шифр Цезаря относятся к моноалфавитной замене: каждая буква заменяется на одну и только одну букву или символ. Такие шифры очень легко расшифровываются с помощью частотного анализа.

Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».

Однако этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов.

Шифр Виженера

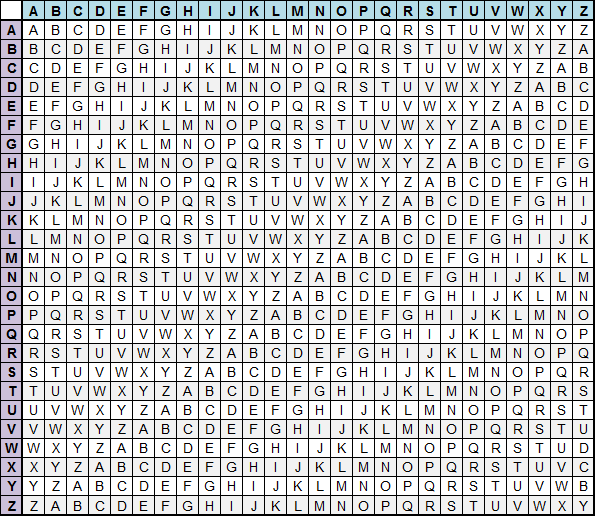
Представим, что есть таблица по типу той, что на картинке, и ключевое слово «CHAIR». Шифр Виженера использует принцип шифра Цезаря, только каждая буква меняется в соответствии с кодовым словом.

В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова «С», вторая буква — для «H», etc. Если послание длиннее кодового слова, то для (k*n+1)-ой буквы, где n — длина кодового слова, вновь будет использован алфавит для первой буквы кодового слова.

Чтобы расшифровать шифр Виженера, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания.

Попробуйте расшифровать эту фразу самостоятельно:

Подсказка длина кодового слова — 4.

Шифр Энигмы

Энигма — это машина, которая использовалась нацистами во времена Второй Мировой для шифрования сообщений.

Есть несколько колёс и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.

Существовало более ста триллионов возможных комбинаций колёс, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.

Цифровые шифры

В отличие от шифровки текста алфавитом и символами, здесь используются цифры. Рассказываем о способах и о том, как расшифровать цифровой код.

Двоичный код

Текстовые данные вполне можно хранить и передавать в двоичном коде. В этом случае по таблице символов (чаще всего ASCII) каждое простое число из предыдущего шага сопоставляется с буквой: 01100001 = 97 = «a», 01100010 = 98 = «b», etc. При этом важно соблюдение регистра.

Расшифруйте следующее сообщение, в котором использована кириллица:

Шифр A1Z26

Это простая подстановка, где каждая буква заменена её порядковым номером в алфавите. Только нижний регистр.

Попробуйте определить, что здесь написано:

Шифрование публичным ключом

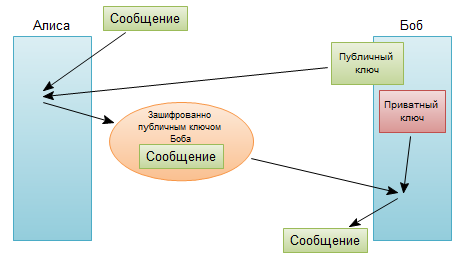
Алгоритм шифрования, применяющийся сегодня буквально во всех компьютерных системах. Есть два ключа: открытый и секретный. Открытый ключ — это большое число, имеющее только два делителя, помимо единицы и самого себя. Эти два делителя являются секретным ключом, и при перемножении дают публичный ключ. Например, публичный ключ — это 1961, а секретный — 37 и 53.

Открытый ключ используется, чтобы зашифровать сообщение, а секретный — чтобы расшифровать.

Как-то RSA выделила 1000 $ в качестве приза тому, кто найдет два пятидесятизначных делителя числа:

Как расшифровать код или шифр?

Для этого применяются специальные сервисы. Выбор такого инструмента зависит от того, что за код предстоит расшифровать. Примеры шифраторов и дешифраторов:

Источник

Простой способ шифрования чисел

Рис.2. Древнегреческий математик Евклид

Теорема Евклида: «Первых простых чисел существует больше любого указанного числа их».

Конечно, способ Эратосфена не смог удовлетворить ученых, и они пытались найти формулу простых чисел. На протяжении многих столетий это сделать не удавалось. В ряду простых чисел были найдены многие интересные закономерности, но поставленная задача оставалась без ответа. Над поиском максимально больших простых чисел в своё время бились Катальди, Декарт, Ферма, Мерсенн, Лейбниц, Эйлер и многие другие математики. В математике широко известен термин простые числа Мерсенна. Простые числа Мерсена являются простыми числами специального вида

где р — другое простое число.

До 1750 года было найдено всего 8 простых чисел Мерсенна: М2, М3, М5, М7, М13, М17, М19, М31. То, что М31 — простое число, доказал в 1750 году Л. Эйлер. В 1876 году французский математик Эдуард Люка установил, что число М127=170141183460469231731687303715884105727 — простое. В 1883 г. сельский священник Пермской губернии И.М.Первушин доказал, что число М61=2305843009213693951 является простым. Позднее было установлено, что числа М89 и М107 простые. 12 простых чисел Мерсена были вычислены с помощью только карандаша и бумаги, а для вычисления следующих уже использовались механические настольные счетные машины.

Масштабный проект по поиску простых чисел GIMPS был запущен в 1997 году, и ныне считается самым длительным непрерывным процессом распределённых вычислений в истории человечества: он продолжается уже почти 20 лет. Сейчас в пиковые моменты в GIMPS участвует 360.000 процессоров с суммарной производительностью 150 трлн операций в секунду. За время работы GIMPS участники этого проекта нашли 14 простых чисел Мерсенна. Последнее из них 274 207 281-1 было обнаружено 07 января 2016 года. Всего на данный момент известно 49 простых чисел Мерсена. В списке самых больших простых чисел, известных на сегодняшний день, десять первых мест занимают числа Мерсенна.

Поиск простых чисел — по крайней мере больших простых чисел — довольно сложная задача, потому что еще никому не удалось найти точную формулу или алгоритм, позволяющий генерировать любые простые числа.

Применение простых чисел в криптографии.

Актуальны ли простые числа сегодня? Еще как! Простые числа являются основой современной криптографии, так что большинство людей пользуются ими каждый день, даже не задумываясь об этом. Любой процесс аутентификации, например, регистрация телефона в сети, банковские платежи и прочее, требуют криптографических алгоритмов.

В 1975 г. Уитфилду Диффи и Мартину Хеллману, в то время работавшим в Стэнфордском университете, пришла в голову идея асимметричного шифрования, или «шифрования с открытым ключом». Эта система основана на специальных математических функциях, называемых «односторонними функциями с потайным входом», которые позволяют зашифровывать текст, но делают расшифровку практически невозможной без знания используемого кода. Идея состоит в том, что каждый пользователь имеет пару ключей: открытый и закрытый. Если мы хотим отправить кому-то сообщение, мы зашифровываем это сообщение с помощью открытого ключа — то есть ключа, известного всем. Но только человек, имеющий соответствующий закрытый ключ, может расшифровать это сообщение. Одним из преимуществ такого метода является то, что закрытый ключ никогда не передается и поэтому его не нужно постоянно менять в целях безопасности. Идея метода не совсем проста, но мы можем пояснить ее с помощью аналогии. Представьте себе большой магазин, где продаются сотни тысяч банок с краской разного цвета. Возьмем две любые банки и смешаем краску в разных количествах. Пока все просто. Теперь, если мы покажем кому-нибудь получившийся цвет и попросим «расшифровать», какое количество каких красок использовалось изначально, на такой вопрос будет очень трудно ответить. Именно так работают односторонние функции с потайным входом, которые легко применить в одном направлении, но практически невозможно — в обратном.

Алгоритм шифрования RSA

В августе 1977 г. знаменитый американский писатель и популяризатор науки Мартин Гарднер озаглавил свою колонку по занимательной математике в журнале Scientific American так: «Новый вид шифра, на расшифровку которого потребуются миллионы лет» [3]. После объяснения принципа системы шифрования с открытым ключом он показал само зашифрованное сообщение и открытый ключ N , используемый в этом шифре:

Гарднер призвал читателей попробовать расшифровать сообщение, используя предоставленную информацию, и даже дал подсказку: для решения необходимо разложить число N на простые множители р и q. Более того, Гарднер назначил приз в размере $100 (приличная сумма на тот момент) тому, кто первым получит правильный ответ. Каждый, кто захочет побольше узнать о шифре, писал Гарднер, может обратиться к создателям шифра — Рону Ривесту, Ади Шамиру и Лену Адлеману из Лаборатории информации Массачусетского технологического института. Правильный ответ был получен лишь через 17 лет. Он стал результатом сотрудничества более чем 600 человек. Ключами оказались р = 32769132993266 709549961988190834461413177642967992942539798288533 и q = 3490529510847650949147849619903898133417764638493387843990820577, а зашифрованная фраза звучала так: «Волшебные слова — это брезгливый ягнятник».

Алгоритм, представленный Гарднером, известен как RSA — буквенная аббревиатура от фамилий Rivest (Ривест), Shamir (Шамир) и Adleman (Адлеман). Это первое практическое применение придуманной Диффи системы шифрования с открытым ключом, которая повсеместно используется и по сей день. Надежность ее практически гарантирована, потому что процесс расшифровки является невероятно сложным, почти невозможным делом.

На сегодняшний день разложить числа, состоящие из тысячи и более цифр, за соизмеримое с человеческой жизнью время, способны только суперкомпьютеры! Именно с их помощью ученные находят все новые и новые, наибольшие из известных, простые числа.

Представим, что один человек, зашифровав важную информацию, установил на нее пароль (P) равный одному из простых делителей числа (А), сказав другому человеку, что число (А) содержит только два простых делителя и дав ему ключ для расшифровки – число (B), являющееся вторым делителем числа (А). Не трудно понять, что для расшифровки необходимо разделить А на B, чтобы получить пароль Р. Например в элементарном варианте А=111, ключ B=3 тогда пароль равен А/B=37.

Допустим, число А попало к злоумышленнику, и он знает условие о том, что А состоит из 2-х простых делителей. При условии, что А=111 злоумышленнику не составит особого труда даже в уме взломать пароль. Теперь представим ситуацию, когда число А состоит из 2 простых чисел, каждое из которых состоит из тысячи цифр… Если злоумышленник не знает ключа (одного из делителей), для факторизации числа А, состоящего из двух тысяч цифр, ему потребуется, как минимум, суперкомпьютер и большое количество времени его работы. Если попытаться попытается разложить произведение — даже при помощи самого быстрого суперкомпьютера — это не получится. Просто не существует такого алгоритма, который справился бы с этой задачей за время жизни Вселенной.

Для применения алгоритма RSA требуется построить открытый и секретный ключи следующим образом.

1. Выбрать два больших простых числа, p и q.

2. Найти их произведение n = p • q и значение ϕ =(р-1)-(q-1)

3. Выбрать число e (1 C = Т e mod n

где Т — число исходного сообщения,

(e, n) — открытый ключ,

С — число закодированного сообщения, а запись С e mod n обозначает остаток от деления x e на n.

Расшифровка сообщения выполняется по формуле

Это значит, что зашифровать сообщение может каждый (открытый ключ общеизвестен), а прочитать его — только тот, кто знает секретный показатель степени d.

В 2009 году группа ученых из разных стран в результате многомесячных расчетов на сотнях компьютеров смогла расшифровать сообщение, зашифрованное алгоритмом. Если будет построен работающий квантовый компьютер, взлом алгоритма RSA будет возможен за очень небольшое время. При использовании симметричных шифров всегда возникает проблема: как передать ключ, если канал связи ненадежный? Ведь, получив ключ, противник сможет расшифровать все дальнейшие сообщения. Для алгоритма RSA этой проблемы нет, сторонам достаточно обменяться открытыми ключами, которые можно показывать всем желающим.

Где применяют алгоритм RSA на практике? Криптосистема RSA используется в самых различных продуктах, на различных платформах и во многих отраслях. В настоящее время криптосистема RSA встраивается во многие коммерческие продукты, число которых постоянно увеличивается. Также ее используют операционные системы Microsoft, Apple, Sun и Novell. В аппаратном исполнении RSA алгоритм применяется в защищенных телефонах, на сетевых платах Ethernet, на смарт-картах, широко используется в криптографическом оборудовании. Кроме того, алгоритм входит в состав всех основных протоколов для защищенных коммуникаций Internet, в том числе S/MIME, SSL и S/WAN, а также используется во многих учреждениях, например, в правительственных службах, в большинстве корпораций, в государственных лабораториях и университетах. На осень 2000 года технологии с применением алгоритма RSA были лицензированы более чем 700 компаниями.

Технологию шифрования RSA BSAFE используют около 500 миллионов пользователей всего мира. Так как в большинстве случаев при этом используется алгоритм RSA, то его можно считать наиболее распространенной криптосистемой общего (public) ключа в мире и это количество имеет явную тенденцию к увеличению по мере роста Internet.

На начало 2001 года криптосистема RSA являлась наиболее широко используемой асимметричной криптосистемой (криптосистемой открытого (public) ключа) и зачастую называется стандартом де факто. Вне зависимости от официальных стандартов существование такого стандарта чрезвычайно важно для развития электронной коммерции и вообще экономики. Единая система открытого (public) ключа допускает обмен документами с электронно-цифровыми подписями между пользователями различных государств, использующими различное программное обеспечение на различных платформах; такая возможность насущно необходима для развития электронной коммерции. Распространение системы RSA дошло до такой степени, что ее учитывают при создании новых стандартов. При разработке стандартов цифровых подписей, в первую очередь в 1997 был разработан стандарт ANSI X9.30, поддерживающий Digital Signature Standard (стандарт Цифровой подписи). Годом позже был введен ANSI X9.31, в котором сделан акцент на цифровых подписях RSA, что отвечает фактически сложившейся ситуации, в частности, для финансовых учреждений.

Для того, чтобы выяснить знают ли ученики 5-х классов о применение простых чисел в кодирование, об алгоритме RSA , а также выявить количество учеников, использующих ежедневно технологию шифрования RSA , я решил провести опрос. Опрос проводился посредством анкетирования. В опросе приняли участие 21 учащийся из 5-х классов МБОУ «Лицей №9 имени К.Э. Циолковского» г. Калуги.

Респондентам были заданы вопросы, представленные в таблице 2.

Источник