Проецирование пятиугольника всеми способами

Содержание

Аксонометрические проекции плоских фигур
Как начертить пятиугольник в изометрии
Проецирование пятиугольника всеми способами
ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ И ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ
ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ, РАСПОЛОЖЕННЫХ НА ПЛОСКОСТИ
ПРОЕКЦИИ ПЛОСКИХ ФИГУР
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
ПРЯМАЯ, ПРИНАДЛЕЖАЩАЯ ПЛОСКОСТИ
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ
ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ

Аксонометрические проекции плоских фигур

Линии X, Y примем за координатные оси. Проводим изометрические оси X р и Y р (рис. 1). Для построения изображения точки 1 достаточно на оси Yр отложить отрезок O р -1, равный по величине координате Y 1 . Затем откладываем в ту же сторону от точки O р отрезок O р -t, равный координате Y 2 , и через точку t проводим прямую ab, параллельную оси X р . Координаты X 2 вершин 2 и 5 пятиугольника одинаковы по величине, но различны по знакам; поэтому на изометрическом изображении откладываем в обе стороны от точки t отрезки t-2 = t-5 = X 2 . Сторона 3-4 пятиугольника параллельна оси X. Отложив от точки q по оси Y р отрезок q-O р , равный координате Y 3 , проводим прямую cd, параллельную оси X р , и откладываем на ней отрезки q-3 = q-4 = X 3 .

Соединив точки 1, 2, 3, 4, 5 прямыми линиями, получаем аксонометрическую проекцию пятиугольника.

Построение аксонометрических проекций плоской кривой сводится к построению проекций ряда ее точек и соединению их в определенной последовательности. На рис. 2 показано построение эллипса, расположенного в плоскости координатных осей X, Y.

построение аксонометрической проекции окружности

При построении аксонометрических проекций часто приходится строить изображения окружностей, расположенных в координатных плоскостях XY, XZ, YZ или в плоскостях, им параллельных. В этом случае нормалями к плоскости окружностей являются соответственно оси Z, Y, X. Следовательно, направления больших осей эллипсов, изображающих проекции окружностей, всегда перпендикулярны соответственно осям Z р , Y р , X р (рис. 4), а малые оси совпадают по направлению с этими осям. Большие оси соответствуют тем диаметрам изображаемых окружностей, которые параллельны картинной плоскости. Если аксонометрическое изображение выполняется с сокращением по направлениям осей X р , Y р , Z р , то большие оси эллипсов 1, 2, 3 (рис. 4) равны диаметру d изображаемых окружностей. В изометрической проекции малые оси эллипсов равны 0,58d. В диметрической проекции малые оси эллипсов 1, 3 (рис.4) равны d/3, а малая ось эллипса 2 равна 0,88d.

При наличии некоторого навыка для вычерчивания эллипса вполне достаточно восьми точек — рис. 5 Точки 1 и 2 — концы большой оси, 3 и 4 — концы малой оси. Точки 5, 6, 7, 8 — аксонометрические проекции концов диаметров окружности, параллельных координатным осям X, Y. Для определения большего количества точек можно применить следующий способ. На кромке полоски бумаги (рис. 5) отложить отрезки AB и AC, равны по величине соответственно большой и малой полуоси эллипса. Если точку С заставить скользить (рис. 5) вдоль большой оси эллипса, а точку B — вдоль малой оси, то точка A опишет эллипс.

В диметрии приближенное вычерчивание эллипса можно производить для окружности, расположенной в плоскости, параллельной XZ и для окружностей, расположенных в плоскостях, параллельных XY и ZY. Порядок вычерчивания показан на рис. 5.

диаграмма умножения размеров на коэффициенты искажения

Проведя две взаимно перпендикулярные прямые AB и AC, на одной из них, например на AB, от точки A откладывают 100 мм. Затем на AC от той же точки A откладывают 35, 50, 70, 95, 106, 122 мм. Полученные точки соединяют с точкой O.
Если от точки O по горизонтали отложить размер l, то взятые по вертикали отрезки Da, Db, . Df равны соответственно 0,35 l; 0,5 l; . ; 1,22 l.

На наклонных линиях диаграммы наносят значения коэффициентов, которым эти линии соответствуют.

Источник

Как начертить пятиугольник в изометрии

Соединив точки 1, 2, 3, 4, 5 прямыми линиями, получаем аксонометрическую проекцию пятиугольника.

построение аксонометрической проекции окружности

При наличии некоторого навыка для вычерчивания эллипса вполне достаточно восьми точек – рис. 5 Точки 1 и 2 – концы большой оси, 3 и 4 – концы малой оси. Точки 5, 6, 7, 8 – аксонометрические проекции концов диаметров окружности, параллельных координатным осям X, Y. Для определения большего количества точек можно применить следующий способ. На кромке полоски бумаги (рис. 5) отложить отрезки AB и AC, равны по величине соответственно большой и малой полуоси эллипса. Если точку С заставить скользить (рис. 5) вдоль большой оси эллипса, а точку B – вдоль малой оси, то точка A опишет эллипс.

диаграмма умножения размеров на коэффициенты искажения

На наклонных линиях диаграммы наносят значения коэффициентов, которым эти линии соответствуют.

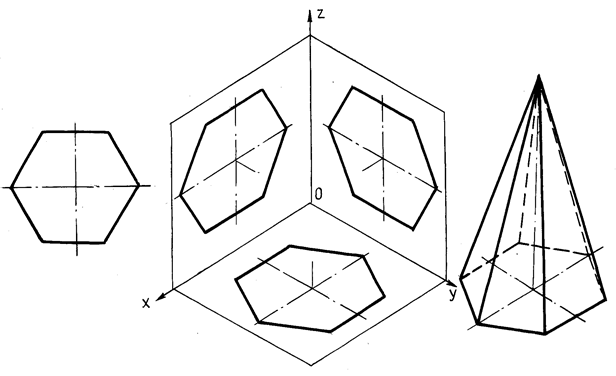
Построение аксонометрических проекций многогранников сводится к определению аксонометрических проекций их вершин, которые затем соединяют между собой отрезками прямых линий. На рис. 72 показано построение изометрической проекции плоской фигуры шестиугольника, расположенного параллельно плоскостям проекций.

Рис. 72. Построение шестиугольника и пирамиды
в прямоугольной изометрии

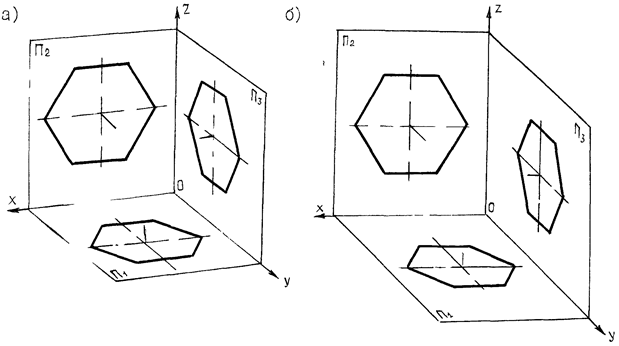
Рис. 73. Аксонометрические проекции шестиугольника:
а – прямоугольная, б – косоугольная диметрии

Рис. 74. Прямоугольная изометрическая проекция
шестигранной призмы

Прямоугольная изометрическая проекция
правильной шестигранной призмы

Построение призмы выполняют в такой последовательности. Если основание призмы – правильный многоугольник (например, шестиугольник), то построение вершин основания по координатам можно упростить, проведя одну из осей координат через центр основания. На рис. 74 оси х, у, z проведены через центры правильных шестиугольников призмы. Построим изометрию основания призмы. Из вершин шестиугольника основания проводим прямые, параллельные соответственно осям x, у или z (для каждой из рассматриваемых на рис. 74 призм). На этих прямых от вершин основания отложим высоту призмы и получим изометрию шести точек 1–6 вершин другого основания призмы. Соединив эти точки прямыми, получим изометрическую проекцию призмы, затем обведем видимые и невидимые линии.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8829 – | 7545 – или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

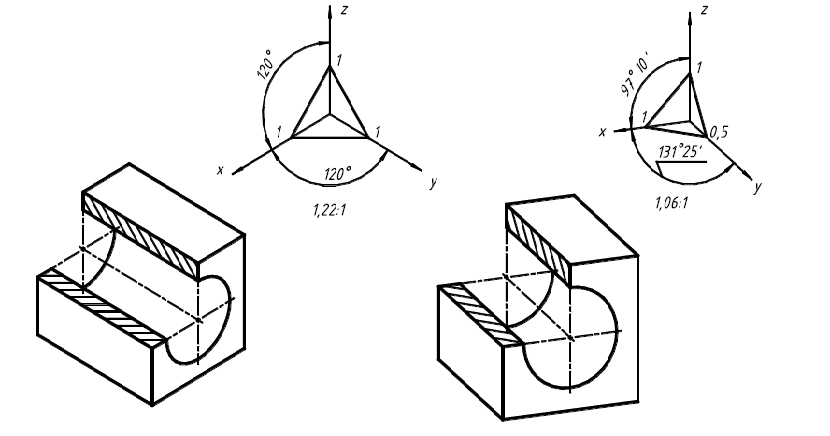
В прямоугольной изометрической проекции оси x, y, z расположены под углом 120º друг к другу. При этом ось z всегда располагается вертикально. Все коэффициенты искажения по аксонометрическим осям одинаковы и равны 0,82, поэтому размеры изображаемого объекта вдоль осей, при создании аксонометрического изображения, должны быть умножены на данный коэффициент искажения. Такая изометрия называется точной или теоретической. Для упрощения обычно применяют приведенную или практическую изометрию, выполненную в масштабе 1,22:1. При этом применяют приведенные коэффициенты искажения, которые равны единице по всем трем осям, что очень удобно при выполнении построении.

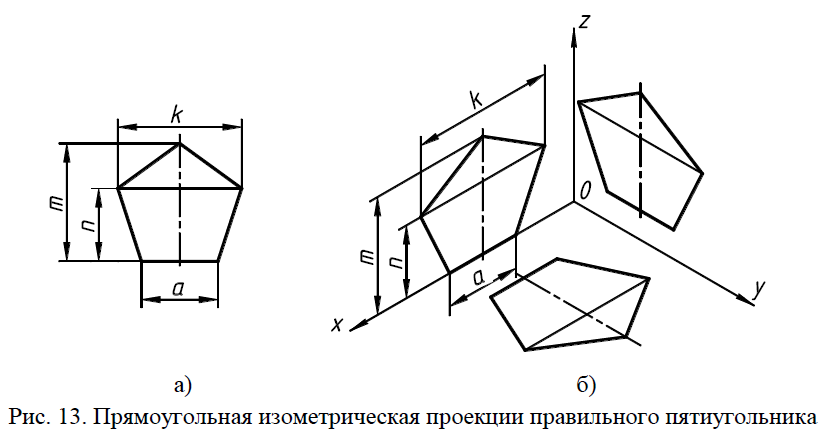
Процесс построения изометрических изображений «плоских» геомет-

рических фигур начинают с построения их исходного изображения.

Например, для построения изометрии правильного пятиугольника сначала необходимо построить его ортогональную проекцию (рис. 20, а), на кото-

рой можно будет замерять необходимые расстояния: a, k, m, n и отклады-

вать их вдоль направления соответствующих координатных осей (рис. 20, б).

Рис. 20. Прямоугольная изометрическая проекция правильного пятиугольника

На рисунке 19, а) изображена изометрическая проекция куба с

окружностями, вписанными в его грани. Квадратные грани куба будут

изображаться в виде ромбов, а окружности – в виде эллипсов. Стоит заметить, что малая ось каждого эллипса всегда перпендикулярна его большой оси.

В зависимости от того, какой плоскости проекций принадлежит эл-

липс, его малая ось будет располагаться параллельно одной из координационных осей. Так, например, если окружность лежит в плоскости XOY,

то его малая ось будет располагаться параллельно оси z, а большая ось будет ей перпендикулярна (рис. 21, а). Аналогично, если эллипс лежит в плоскости XOZ, то малая ось параллельна оси y, а если эллипс в YOZ, то малая ось сонаправлена с осью x. При этом длина малой оси равна 0,71d, где d – диаметр изображаемой окружности, а большая ось – 1,22d (рис. 21, б).

Рис.21. Прямоуголная изометрическая проекция окружности

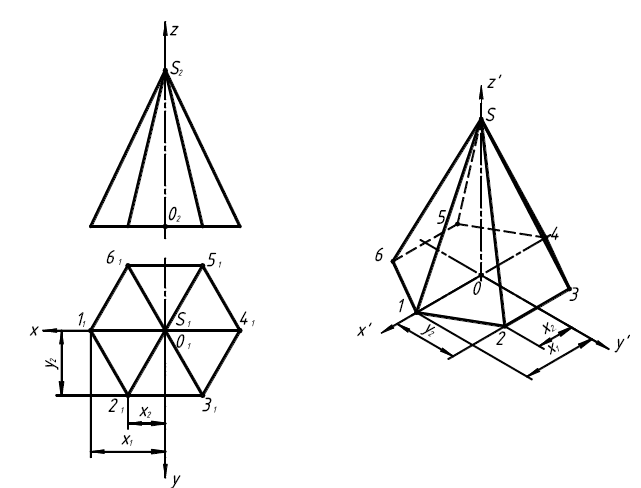
Построение изометрических проекций геометрических тел, в частно-

сти многогранников, сводится к определению аксонометрических проекций их вершин, которые затем соединяются между собой отрезками прямых линий.

На рисунке 22 показано построение изометрического изображения правильной шестигранной пирамиды, основание которой лежит в плоскости XOY, а высота пирамиды совпадает с осью z, по ее ортогональным проекциям (рис. 22, а).

Рис. 22. Прямоугольная изометрия правильной шестиугольной пирамиды

Очень часто для повышения наглядности аксонометрического изоб-

ражения выполняются разрезы изображаемого объекта, то есть предмет изображают с удаленной некоторой ее частью (рис. 23). При этом секущие плоскости располагаются параллельно координатным плоскостям. Для обозначения материала предмета в разрезе наносят штриховку

Рис. 23. Аксонометрические проекции детали с четвертью выреза

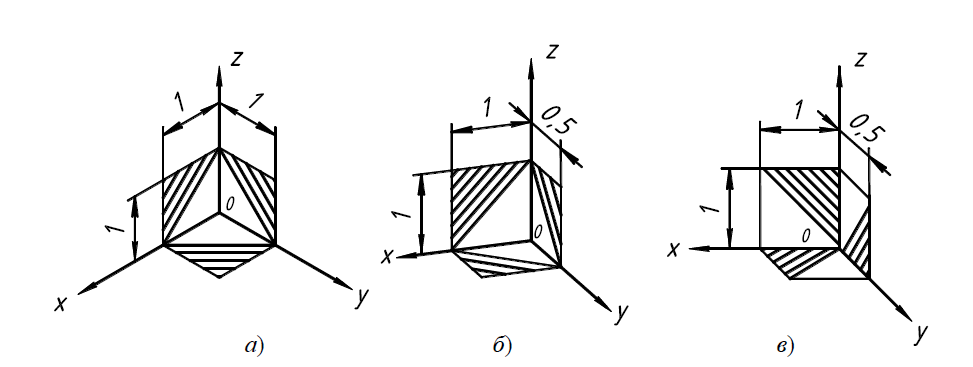
Линии штриховки наносятся параллельно одной из диагоналей квад-

ратов, лежащих в соответствующих координатных плоскостях (рис. 24).

Рис. 24. Штриховка на аксометрических изображениях

а) в прямоугольной изометрии; б) в прямоугольной диметрии;

в) в косоугольной диметрии

Аксонометрические изображения является достаточно наглядными.

Однако перспектива наиболее реалистичнее передает видимый нами объект, так как аппарат центрального проецирования более всего соответствует аппарату человеческого глаза, но перспективные проекции являются и наиболее трудными для построения.

Источник

Проецирование пятиугольника всеми способами

Плоскостью называется поверхность, образуемая движением прямой линии, которая движется параллельно самой себе по неподвижной направляющей прямой .

Проекции плоскости на комплексном чертеже будут различны в зависимости от того, чем она задана. Как известно из геометрии, плоскость может быть задана: а) тремя точками, не лежащими на одной прямой; б) прямой линией и точкой, лежащей вне этой прямой; в) двумя пересекающимися прямыми; г) двумя параллельными прямыми.

На комплексном чертеже (рис. 99) проекции плоскости также задаются проекциями этих элементов, например, на рис 99, а — проекциями трех точек А, , и С, не лежащих на одной прямой; на рис. 99, б — проекциями прямой ВС и точки А у не лежащей на этой прямой; на рис. 99, в — проекциями двух пересекающихся прямых; на рис. 99, г проекциями двух параллельных прямых линий АВ и CD.

На рис. 100 плоскость задана прямыми линиями, по которым эта плоскость пересекает плоскости проекций. Такие линии называются следами плоскости.
Линия пересечения данной плоскости Р с горизонтальной плоскостью проекций Н называется горизонтальным следом плоскости Р и обозначается Р_н.
Линия пересечения плоскости Р с фронтальной плоскостью проекций V называется фронтальным следом этой плоскости и обозначается Р_v.

Линия пересечения плоскости Р с профильной плоскостью проекций W называется профильным следом этой плоскости и обозначается P_w.

Следы плоскости пересекаются на осях проекций. Точки пересечения следов плоскости с осями проекций называются точками схода следов. Эти точки обозначаются Р_x, Р_y и Р_z.

Расположение следов плоскости Р на комплексном чертеже по отношению к осям проекций определяет положение самой плоскости по отношению к плоскостям проекций. Например, если плоскость Р имеет фронтальный и профильный следы P_v и P_w, параллельные осям Ох и Оу то такая плоскость параллельна плоскости Н и называется горизонтальной (рис. 101, и). Плоскость Р со следами Р_н и P_w , параллельными осям проекций Ох и Oz (рис. 101, называется фронтальной, а плоскость Р со следами P_v и P_н параллельными осям проекций Оу и Oz, — профильной (рис. 101, в).

Горизонтальная, фронтальная и профильная плоскости, перпендикулярные к двум плоскостям проекций, называются плоскостями уровня. Если на комплексном чертеже плоскость уровня задана не следами, а какой-нибудь плоской фигурой, например, треугольником или параллелограммом (рис. 101, г, д, е), то на одну из плоскостей проекций эта фигура проецируется без искажения, а на две другие плоскости проекций — в виде отрезков прямых.

ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ И ПЛОСКОСТЬ ОБЩЕГО ПОЛОЖЕНИЯ

Плоскость, перпендикулярная к плоскости Н (рис. 102, а),называется горизонтально-проецирующей плоскостью. Фронтальный след P_v этой плоскости перпендикулярен оси Ох, а горизонтальный след Р_н расположен под углом к оси Ох (комплексный чертеж на рис. 102, а)

Если горизонтально-проецирующая плоскость задана не следами, а какой-либо фигурой, например треугольником АВС (рис. 102, 6), то горизонтальная проекция этой плоскости представляет собой прямую линию, а фронтальная и профильная проекции — искаженный вид треугольника АВС.

Фронтально-проецирующей плоскостью называется плоскость, перпендикулярная к фронтальной плоскости проекций (рис. 102, в).

Горизонтальный след этой плоскости перпендикулярен оси Ох, а фронтальный след расположен под некоторым углом к оси Ох (комплексный чертеж на рис. 102, в).

При задании фронтально-проецирующей плоскости не следами, а, например, параллелограммом ABCD фронтальная проекция такой плоскости представляет собой прямую линию (рис. 102, г), а на горизонтальную и профильную плоскости проекций параллелограмм проецируется с искажением.

Профильно-проецирующей плоскостью называется плоскость, перпендикулярная к плоскости W (рис. 102, д). Следы P_v и Р_н этой плоскости параллельны оси Ох.

При задании профильно-проецирующей плоскости не следами, а, например, треугольником АВС (рис. 102, е) профильная проекция такой плоскости представляет собой прямую линию. Плоскости, перпендикулярные двум плоскостям проекций, как было сказано, называются плоскостями уровня.

Если плоскость Р не перпендикулярна ни одной из плоскостей проекций (рис. 102, ж), то такая плоскость называется плоскостью общего положения. Все три

следа P_v, Р_н и P_w плоскости Р наклонены к осям проекций.

Если плоскость общего положения задана не следами, а, например, треугольником АВС (рис. 102, з), то этот треугольник проецируется на плоскости H, V и W в искаженном виде.

ПРОЕКЦИИ ТОЧКИ И ПРЯМОЙ, РАСПОЛОЖЕННЫХ НА ПЛОСКОСТИ

Если прямая расположена на плоскости, то она должна проходить через две какие-либо точки, принадлежащие этой плоскости. Такие две точки могут быть взяты на следах плоскости — одна на горизонтальном, а другая на фронтальном. Так как следы прямой и плоскости находятся на плоскостях проекций и то следы прямой, принадлежащей плоскости, должны быть расположены на одноименных следах этой плоскости (рис. 103, а);например, горизонтальный след Н прямой — на горизонтальном следе плоскости, фронтальный след V прямой — на фронтальном следе Рv плоскости (рис. 103, б).

Для того чтобы на комплексном чертеже плоскости Р, заданной следами, провести какую-либо прямую общего положения, необходимо наметить на следах плоскости точки v’ или считать их следами искомой прямой (точнее, v’ — фронтальной проекцией горизонтального следа прямой).

Опустив перпендикуляры из v’ и на ось проекций х, находим на ней вторые проекции следов прямой: v — горизонтальную проекцию фронтального следа прямой и h’ — фронтальную проекцию горизонтального следа прямой. Соединив одноименные проекции следов, т. е. v’c h и v c h прямыми, получим две проекции прямой линии, расположенной в плоскости общего положения Р.

Очень часто требуется провести на плоскости горизонталь и фронталь, которые называются главными линиями плоскости или линиями уровня. Главные линии помогают решать многие задачи проекционного черчения.

Горизонталь и фронталь имеют в системе двух плоскостей V и Н только по одному следу (например, горизонталь имеет только фронтальный след). Поэтому, зная один след главной линии, проекцию главной линии проводят по заранее известному направлению. Это направление для горизонтали видно из рис. 104, а, где показана плоскость общего положения и горизонталь, лежащая на ней. Из рисунка видно, что горизонтальная проекция горизонтали параллельна горизонтальному следу плоскости.

Таким образом, чтобы на комплексном чертеже плоскости Р провести в этой плоскости какую-либо горизонталь, нужно наметить на следе Р_v плоскости точку v’ (рис. 104, б) и считать ее фронтальной проекцией фронтального следа горизонтали. Затем через точку v’ параллельно оси х проводят прямую, которая будет фронтальной проекцией горизонтали.

Опустив перпендикуляр из точки v’ на ось x , получают точку v, которая будет горизонтальной проекцией фронтального следа горизонтали. Прямая, проведенная из точки v параллельно следу P_H плоскости, представляет собой горизонтальную проекцию искомой горизонтали. Построение проекции фронтали показано на рис. 104, в и г.

11 с редко требуется провести горизонталь и фронталь на проецирующих плоскостях. Рассмотрим, например, построение горизонтали на фронтально-проецирующей плоскости (рис. 105). На следе плоскости Р_v намечаем фронтальную проекцию фронтального следа горизонтали и на оси находим его горизонтальную проекцию v (рис. 105, а). Затем через точку проводим параллельно Р_н горизонтальную проекцию горизонтали; фронтальная проекция горизонтали совпадает с точкой v’.

Если плоскость задана не следами, а пересекающимися или параллельными прямыми, то построение проекций горизонтали или фронтали, расположенных в этой плоскости, выполняется следующим образом.

Пусть плоскость задана двумя параллельными прямыми AВ и СD (рис. 105, 6). Для построения горизонтали, лежащей в этой плоскости, проводим параллельно оси х фронтальную проекцию горизонтали и отмечаем точки е’и f’ пересечения фронтальной проекции горизонтали с фронтальными проекциями параллельных прямых, которыми задана плоскость. Через точки е’и f’ проводим вертикальные линии связи до пересечения с ab и cd в точках е и f. Точки е и f соединяем прямой линией, которая и будет горизонтальной проекцией горизонтали.

Если требуется найти следы плоскости, заданной пересекающимися или параллельными прямыми, надо найти следы этих прямых и через полученные точки провести искомые следы плоскости.

Рассмотрим комплексный чертеж параллелограмма ABCD (рис. 106, a),который задает некоторую плоскость X. Отрезок DC расположен в плоскости H, следовательно, его горизонтальная проекция dc является горизонтальным следом плоскости (точнее — горизонтальной проекцией горизонтального следа плоскости).

Чтобы найти фронтальный след этой плоскости, необходимо продолжить горизонтальную проекцию dc прямой DC до пересечения с осью х в точке Р_х, через которую должен пройти искомый фронтальный след плоскости.

Второй точкой v’, через которую пройдет искомый фронтальный след плоскости, является фронтальный след прямой АВ (фронтальная проекция фронтального следа). Фронтальную проекцию фронтального следа прямой АВ находим, продолжая горизонтальную проекцию ab прямой АВ до пересечения с осью х в точке v, которая будет горизонтальной проекцией искомого фронтального следа прямой АВ. Фронтальная проекция фронтального следа этой прямой находится на перпендикуляре, восставленном из точки v к оси х, в точке v’ его пересечения с продолжением фронтальной проекции а’в’ прямой АB. Соединив точки P_x с v’, находим фронтальный след P_v плоскости.

Пример решения подобной задачи приведен на рис 106, б.

Часто на комплексных чертежах приходится решать такую задачу: по одной из заданных проекций точки, расположенной на заданной плоскости, определить две другие проекции точки. Ход решения задачи следующий.

Через заданную проекцию точки, например фронтальную проекцию n’ точки N, расположенной на плоскости треугольника АВС (рис. 107), проводим одноименную проекцию вспомогательной прямой любого направления, например m’к’.

Горизонталью плоскости называется прямая, принадлежащая этой плоскости и параллельная горизонтальной плоскости проекций Н.

Строим другую проекцию mк вспомогательной прямой. Для этого проводим вертикальные линии связи через точки m’ и к’ до пересечения с линиями ас и вс. Из точки n’ проводим линию связи до пересечения с проекцией mк в искомой точке n.

Профильную проекцию n» находим по общим правилам проецирования.

В качестве вспомогательной прямой для упрощения построения чаще используются горизонталь или фронталь.

Чтобы найти какую-либо точку на плоскости Р, например точку А (рис. 108, а и б) надо найти ее проекции а’и а, которые располагаются на одноименных проекциях горизонтали, проходящей через эту точку. Через точку А проведена горизонталь Av’ .

Проводим проекции горизонтали: фронтальную — через v’ параллельно оси х, горизонтальную — через v параллельно следу Р_н плоскости Р. На фронтальной проекции горизонтали намечаем фронтальную проекцию а’ искомой точки и, проводя вертикальную линию связи, определяем горизонтальную проекцию а точки А.

Если точка лежит на проецирующей плоскости, то построение ее проекций упрощается. В этом случае одна из проекций точки всегда расположена на следу плоскости (точнее, на его проекции). Например, горизонтальная проекция а точки А, расположенной на горизонтально-проецирующей плоскости Р, находится на горизонтальной проекции горизонтального следа плоскости (рис. 108, в и г)

При заданной фронтальной проекции a’ точки А, лежащей на горизонтально-проецирующей плоскости , найти вторую проекцию этой точки (горизонтальную) можно без вспомогательной прямой, посредством проведения линии связи через а’ до пересечения со следом Р_Н.

Если точка расположена на фронтально-проецирующей плоскости Р (рис. 108, д и е), то ее фронтальная проекция а’ находится на фронтальном следе Х_v плоскости Р.

ПРОЕКЦИИ ПЛОСКИХ ФИГУР

Зная построение проекций прямых и точек, расположенных на плоскости, можно построить проекции любой плоской фигуры, например, прямоугольника, треугольника, круга.

Как известно, каждая плоская фигура ограничена отрезками прямых или кривых линий, которые могут быть построены по точкам.

Проекции фигуры, ограниченной прямыми линиями (треугольника и многоугольника), строят по точкам (вершинам). Затем одноименные проекции вершин соединяют прямыми линиями и получают проекции фигур.

Проекции круга или другой криволинейной фигуры строят при помощи нескольких точек, которые берут равномерно по контуру фигуры. Одноименные проекции точек соединяют плавной кривой по лекалу.

Проекции плоской фигуры строят различными способами в зависимости от положения фигуры относительно плоскостей проекций и Наиболее просто построить проекции фигуры, расположенной параллельно плоскостям Н и V; сложнее — при расположении фигуры на проецирующей плоскости или на плоскости общего положения.

Рассмотрим несколько примеров.

Если треугольник АВС расположен на плоскости, параллельной плоскости H (рис. 109, a), то горизонтальная проекция этого треугольника будет его действительным видом, а фронтальная проекция — отрезком прямой, параллельным оси х. Комплексный чертеж треугольника АВС показан на рис. 109, 6. Такой треугольник можно видеть на изображении резьбового резца (рис. 109, в),передняя грань которого треугольная.

Трапеция ABCD расположена на фронтально-проецирующей плоскости (рис. 110, а). Фронтальная проекция трапеции представляет собой отрезок прямой линии, а горизонтальная — трапецию (рис. 110, б)

Задняя грань отрезного резца (рис. 110, в) имеет форму трапеции.

Рассматривая плоскость, параллельную горизонтальной, фронтальной или профильной плоскости проекций (плоскость уровня), можно заметить, что любая фигура, лежащая в этой плоскости, имеет одну из проекций, представляющую собой действительный вид этой фигуры; вторая и третья проекции фигуры совпадают со следами этой плоскости.

Рассматривая проецирующую плоскость, заметим, что любая точка, отрезок прямой или кривой линии, а также фигуры, расположенные на проецирующей плоскости, имеют одну проекцию, расположенную на следе этой плоскости. Например, если круг лежит на фронтально-проецирующей плоскости Р (рис. 111), то фронтальная проекция круга совпадает с фронтальным следом Pv плоскости Р. Две другие проекции круга искажены и представляют собой эллипсы. Большие оси эллипсов равны проекциям диаметра круга 37. Малые оси эллипсов равны проекциям диаметра круга 15, перпендикулярного диаметру 37.

На рис. 111,6 показано колено трубы с двумя фланцами. Горизонтальная проекция контура нижнего фланца, который расположен в горизонтальной плоскости, будет действительным видом окружности. Горизонтальная проекция контура верхнего фланца изобразится в виде эллипса.

ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

Две плоскости могут быть взаимно параллельными или пересекающимися.

Из стереометрии известно, что если две параллельные плоскости пересекают какую-либо третью плоскость, то линии пересечения этих плоскостей параллельны между собой. Исходя из этого положения, можно сделать вывод, что одноименные следы двух параллельных плоскостей Р и Q также параллельны между собой.

Если даны две профильно-проецирующие плоскости Р и К (рис. 112, а), то параллельность их фронтальных и горизонтальных следов на комплексном чертеже в системе V и Н недостаточна для того, чтобы определить, параллельны эти плоскости или нет. Для этого необходимо построить их профильные следы в системе V, Н и W (рис. 112, б). Плоскости Р и K будут параллельны только в том случае, если параллельны их профильные следы P_w и K_w.

Одноименные следы пересекающихся плоскостей Р и Q (рис. 112, в) пересекаются в точках V и H, которые принадлежат обеим плоскостям, т. е. линии их пересечения. Так как эти точки расположены на плоскостях проекций, то, следовательно, они являются также следами линии пересечения плоскостей. Чтобы на комплексном чертеже построить проекции линии пересечения двух плоскостей Р и Q, заданных следами P_v, Р_н и Q_v,Q_h, необходимо отметить точки пересечения одноименных следов плоскостей, т. е. точки v’ и h (рис. 112, г); точка v’ — фронтальная проекция фронтального следа искомой линии пересечения плоскостей Р и Q, h — горизонтальная проекция горизонтального следа этой же прямой. Опуская перпендикуляры из точек v’ и h на ось х, находим точки v и h’. Соединив прямыми одноименные проекции следов, т. е. точки v’ и h’, v и h’ получим проекции линии пересечения плоскостей Р и Q.

ПРЯМАЯ, ПРИНАДЛЕЖАЩАЯ ПЛОСКОСТИ

Для этого фронтальную проекцию отрезка m’n’ продолжаем до пересечения с отрезками a’b’ и c’d’ (проекциями сторон треугольника АВС), получаем точки (рис. 113, б).

Из точек е’к’ проводим линии связи на горизонтальную проекцию до пересечения с отрезками ab и ca , получаем точки еk. Продолжим горизонтальную проекцию mn отрезка прямой MN до пересечения с проекциями сторон bа и са, если точки пересечения совпадут с ранее полученными точками e и k то прямая MN принадлежит плоскости треугольника.

ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПЛОСКОСТЬЮ

Если прямая АВ пересекается с плоскостью Р, то на комплексном чертеже точка их пересечения определяется следующим образом.

Через прямую А В проводят любую вспомогательную плоскость Q. Для упрощения построений плоскость Q обычно берется проецирующей (рис. 114, a). В данном случае проведена вспомогательная горизонтально-проецирующая плоскость Q. Через горизонтальную проекцию аb прямой АВ проводят горизонтальный след Q_H плоскости Q и продолжают его до пересечения с осью x в точке Q_x . Из точки Q_x к оси х восставляют перпендикуляр Q_xQ_y , который будет фронтальным следом Q_v вспомогательной плоскости Q.

Вспомогательная плоскость Q пересекает данную плоскость Р по прямой VH, следы которой лежат на пересечении следов плоскостей Р и Q. Заметив точки пересечения следов P_v и Q_v — точку v’ и следов Q_н и P_H — точку h,опускают из этих точек на ось х перпендикуляры, основания которых — точки v’ и h’ — будут вторыми проекциями следов прямой VH. Соединяя точки v’и h’, v и h, получают фронтальную и горизонтальную проекции линии пересечения плоскостей.

Точка пересечения М заданной прямой AB и найденной прямой VH и будет искомой точкой пересечения прямой АВ с плоскостью Р. Фронтальная проекция m’ этой точки расположена на пересечении проекций a’b’ и v’h’. Горизонтальную проекцию m точки М находят, проводя вертикальную линию связи из точки m’ до пересечения с ab.

Если плоскость задана не следами, а плоской фигурой, например, треугольником (рис. 114, 6), то точку пересечения прямой MN с плоскостью треугольника АВС находят следующим образом.

Через прямую МN проводят вспомогательную фронтально-проецирующую плоскость . Для этого через точки m’ и n’ проводят фронтальный след плоскости Р_у продолжают его до оси x и из точки пересечения следа плоскости Р_у с осью х опускают перпендикуляр Р_н, который будет горизонтальным следом плоскости Р.

Затем находят линию ED пересечения плоскости Р с плоскостью данного треугольника ABC. Фронтальная проекция e’d’ линии ED совпадает с m’n’. Горизонтальную проекцию ed находят, проводя вертикальные линии связи из точек е’и d’ до встречи с проекциями ab и ас сторон треугольника АВС. Точки e и d соединяют прямой. На пересечении горизонтальной проекции ed линии ED с горизонтальной проекцией прямой MN находят горизонтальную проекцию k искомой точки К. Проведя из точки k вертикальную линяю связи, на ходят фронтальную проекцию k’ Точка К — искомая точка пересечения прямой МК с плоскостью треугольника АВС.

В частном случае прямая может быть перпендикулярна плоскости Р.Из условия перпендикулярности прямой к плоскости следует, что прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим на этой плоскости (в частности, этими прямыми могут быть следы плоскости). Тогда проекции прямой АВ будут перпендикулярны одноименным следам этой плоскости (рис 115, а) Фронтальная проекция а’b’ перпендикулярна фронтальному следу Р_у, а горизонтальная проекция ab перпендикулярна горизонтальному следу Р_н плоскости Р.

Если плоскость задана параллельными или пересекающимися прямыми, то проекции прямой, перпендикулярной этой плоскости, будут перпендикулярны горизонтальной проекции горизонтали и фронтальной проекции фронтали, лежащих на плоскости.

Таким образом, если, например, на плоскость, заданную треугольником АВС необходимо опустить перпендикуляр, то построение выполняется следующим образом (рис. 115, б).

На плоскости проводят горизонталь СЕ и фронталь FA. Затем из заданных проекций d и d’ точки D опускают перпендикуляры соответственно на ce и f’a’. Прямая, проведенная из точки D будет перпендикулярна плоскости треугольника АВС.

ПЕРЕСЕЧЕНИЕ ПЛОСКОСТЕЙ

Задачи на построение линии пересечения плоскостей, заданных пересекающимися прямыми, можно решать подобно задаче на пересечение плоскости с прямыми линиями. На рис. 116 показано построение линии пересечения плоскостей, заданных треугольниками АВС и DEF. Прямая MN построена по найденным точкам пересечения сторон DE и EF треугольника DEF с плоскостью треугольника АВС.

Например, чтобы найти точку M, через прямую DF проводят фронтально-проецирующую плоскость Р, которая пересекается с плоскостью треугольника АВС по прямой 12. Через полученные точки 1′ и 2′ проводят вертикальные линии связи до пересечения их с горизонтальными проекциями ав и ас сторон треугольника АВС в точках 1 и 2. На пересечении горизонтальных проекций df и 12 получают горизонтальную проекцию m искомой точки М, которая будет точкой пересечения прямой DF с плоскостью АВС. Затем находят фронтальную проекцию m’ точки M. Точку N пересечения прямой EF с плоскостью АВС находят так же, как и точку М.

Соединив попарно точки m’ и n’, m и n, получают проекции линий пересечения MN плоскостей АВС и DEF.

Источник