Графический способ умножения
Исследовательский проект по математике НПК «Первые шаги в науку» школьный этап
Скачать:
| Вложение | Размер |
|---|---|
| Графический способ умножения (презентация) | 2.45 МБ |
| Графический способ умножения (доклад) | 1.85 МБ |
Предварительный просмотр:
Подписи к слайдам:
Графический способ умножения Выполнили: Блинова Алиса, Афанасьева Анна ученики 5 класса «А» Руководитель: Галайджян Андрей Сетракович , учитель математики МОУ СОШ № 28
Цель исследования: изучить графический способ умножения Задачи: изучить литературу по данной теме; провести анкетирование по теме исследования; научиться применять графический способ умножения; научить одноклассников использовать этот способ при вычислениях; апробировать графический способ умножения в 1А и 5А классах.
Вычислить 6 7 2
Пример 1. Вычислить
Пример 2. Вычислить
Апробация графического способа умножения в 1А классе .
Апробация графического способа умножения в 1А классе .
Апробация графического способа умножения в 1А классе .
Апробация графического способа умножения в 1А классе .
Апробация графического способа умножения в 1А классе .
Апробация графического способа умножения в 1А классе .
Апробация графического способа умножения в 1А классе .
Спасибо за внимание!
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Павел Петрович Бажов. Хрупкая веточка
Чем пахнут ремёсла? Джанни Родари
Кто чем богат, тот тем и делится!
Астрономы получили первое изображение черной дыры
Источник
Графический способ умножения

Данная презентация расчитана на защиту учебного проекта по математике «Графический способ умножения»
Просмотр содержимого документа
«Графический способ умножения»
Выполнила: Снопок Дарья
ученица 5 класса
МАОУ НГО «СОШ № 12»
Руководитель: Жвакина Анастасия Михайловна
учитель МАОУ НГО «СОШ № 12»
- Изучить графический способ умножения чисел и его применение при вычислениях числовых выражений.
- Разобрать данный способ умножения.
- Рассказать о новом способе умножения и научить им пользоваться других.
- Развить навыки графического способа умножения.
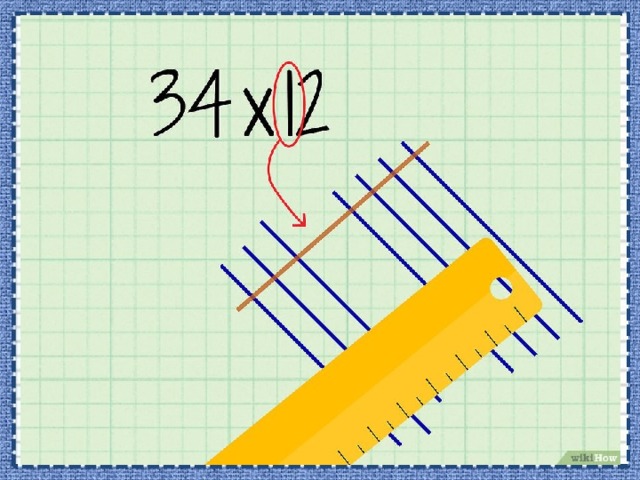
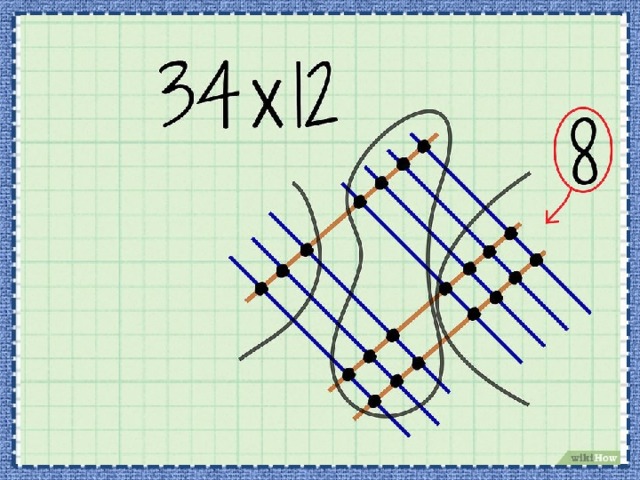
- Определите разряды цифр первого числа. Нужно определить количество разрядов и разряды каждой цифры.
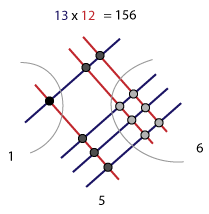
• Например, нужно перемножить . У числа 34 цифра 4 стоит в разряде единиц, а цифра 3 – в разряде десятков.
- Нарисуйте параллельные линии, представляющие разряд десятков первого числа. Количество линий соответствует цифре, которая стоит в разряде десятков.
• Нарисуйте наклонные линии (под углом в 45 градусов), которые убывают слева направо.
• Например, в случае числа 34 нарисуйте 3 параллельные линии.
- Нарисуйте параллельные линии, представляющие разряд единиц первого числа. Количество линий соответствует цифре, которая стоит в разряде единиц. Эти линии нарисуйте справа и выше линий, представляющих разряд десятков.
• Между линиями разряда десятков и линиями разряда единиц оставьте пустое пространство, чтобы отличать их.
• Например, в случае числа 34 нарисуйте 4 параллельные линии.
- Определите разряды цифр второго числа. Нужно определить количество разрядов и разряды каждой цифры.
- • В нашем примере у числа 12 цифра 2 стоит в разряде единиц, а цифра 1 – в разряде десятков.
- Нарисуйте параллельные линии, представляющие разряд десятков второго числа. Количество линий соответствует цифре, которая стоит в разряде десятков. Линии проведите в верхней части линий первого числа. Линии второго числа должны пересекать линии первого числа и возрастать справа налево.
- • Лучше нарисовать линии первого и второго чисел разными цветами.
• Например, в случае числа 12 нарисуйте 1 линию.
- Нарисуйте параллельные линии, представляющие разряд единиц второго числа. Количество линий соответствует цифре, которая стоит в разряде единиц. Эти линии нарисуйте справа и ниже линий, представляющих разряд десятков. Линии второго числа должны пересекать линии первого числа и возрастать справа налево.
- Между линиями разряда десятков и линиями разряда единиц оставьте пустое пространство, чтобы отличать их.
- Например, в случае числа 12 нарисуйте 2 параллельные линии.
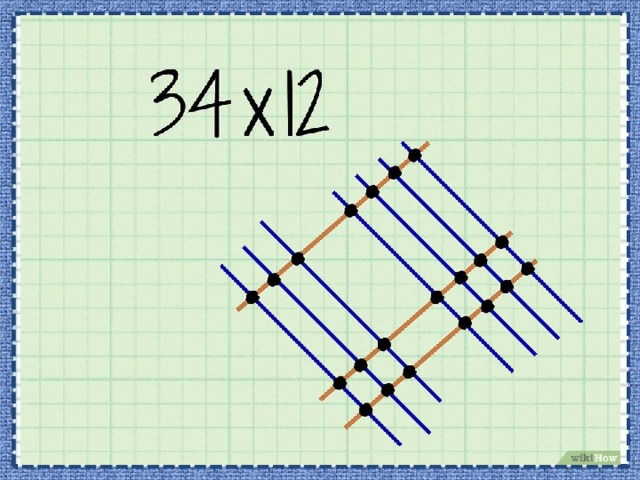
- Отметьте точки пересечений линий. Графический способ умножения подразумевает сложение точек, а не умножение чего-либо.
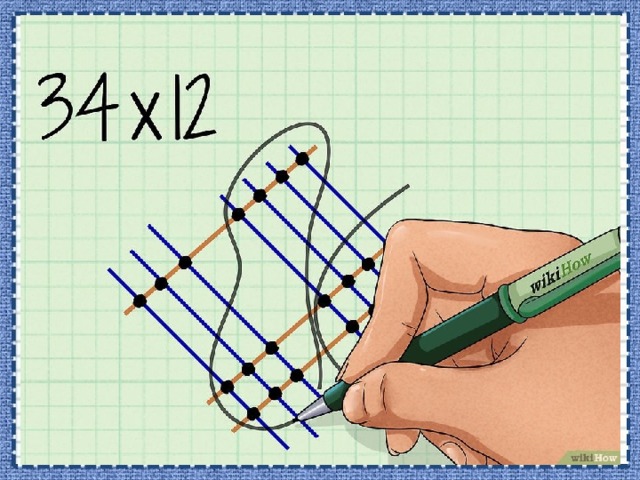
- Обведите точки, представляющие разряд единиц. Это точки пересечения линий разряда единиц первого и второго чисел.
- Вспомните, что 1 умножить на 1 равно 1.
- В нашем примере ( обведите точки пересечения четырех линий с двумя линиями (правая часть рисунка).
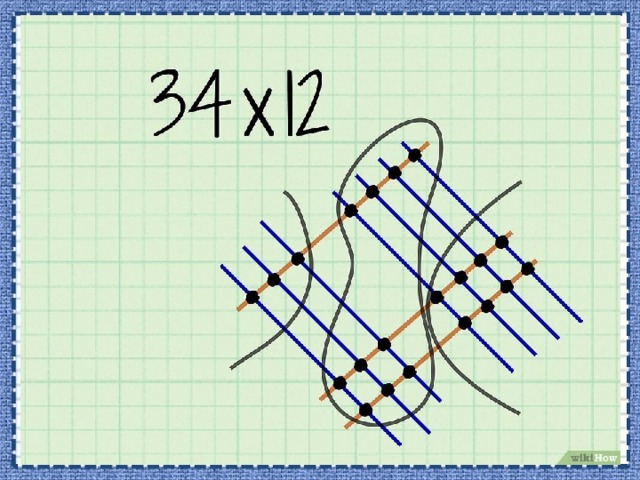
- Обведите точки, представляющие разряд десятков. Это точки пересечения линий разряда десятков (первого или второго числа) с линиями разряда единиц (первого или второго числа).
- Вспомните, что 1 умножить на 10 равно 10.
- В нашем примере обведите точки пересечения одной линии с четырьмя линиями (верхняя часть рисунка) и точки пересечения двух линий с тремя линиями (нижняя часть рисунка).
- Обведите точки, представляющие разряд сотен. Это точки пересечения линий разряда десятков первого и второго чисел.
- Вспомните, что 10 умножить на 10 равно 100.
- В нашем примере обведите точки пересечения трех линий с одной линией (левая часть рисунка).
- Сложите точки разряда единиц. Эти точки обведены в правой части рисунка. Полученную цифру запишите в разряд единиц конечного ответа.
- В нашем примере вы насчитаете 8 точек разряда единиц. Таким образом, 8 – это цифра, которая будет стоять в разряде единиц конечного числа.
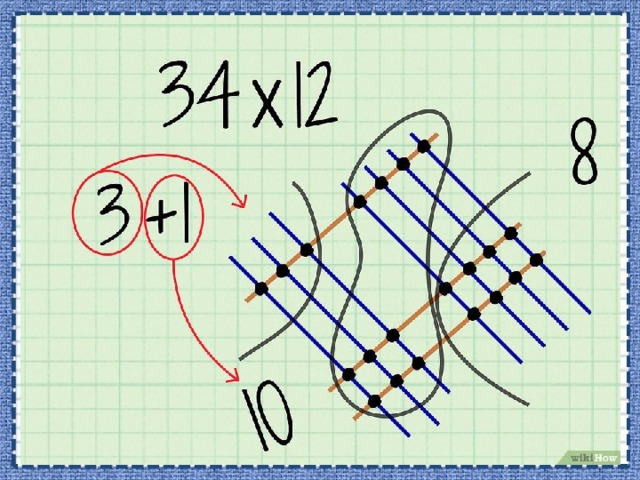
- Сложите точки разряда десятков. Эти точки обведены в верхней и нижней частях рисунка. Полученную цифру запишите в разряд десятков конечного ответа.
- В нашем примере вы насчитаете 10 точек разряда десятков.
- Вспомните, что если в операции сложения или умножения получилось двузначное число, применяется перенос цифр. Вы насчитали 10 точек; таким образом, 0 запишите в разряд десятков, а 1 перенесите в разряд сотен (конечного числа).
- Сложите точки разряда сотен. Эти точки обведены в левой части рисунка. Полученную цифру запишите в разряд сотен конечного ответа.
- В нашем примере вы насчитаете 3 точки разряда сотен.
- Не забудьте прибавить перенесенную цифру. В нашем примере из разряда десятков в разряд сотен перенесли 1, поэтому 3+1=4. Таким образом, запишите 4 в разряд сотен конечного числа.
- Запишите окончательный ответ. Запишите цифры (рядом друг с другом), найденные для каждого разряда.
- В нашем примере вы нашли, что цифра 8 должна стоять в разряде единиц, цифра 0 – в разряде десятков, цифра 4 – в разряде сотен. Таким образом, окончательный ответ: 408.
Источник
Проектная работа «Способы умножения чисел»
данная работа представляет собой проектную работу по математике.
Содержимое разработки
Научно практическая конференция школьников
« Необычные способы умножения»
Над проектом работал:
Ученик 5 В класса
Руководитель проекта: Трученкова Ю.В.
Учитель математики МОУ-СОШ №3
Цель и задачи проекта:
Цель: ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.
Задачи: Найти и разобрать различные способы умножения.
Научиться демонстрировать некоторые способы умножения.
Рассказать о новых способах умножения и научить ими пользоваться учащихся.
Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.
Эксперимент «какой способ быстрей»
Гипотеза: Надо ли знать таблицу умножения?
Актуальность: В последнее время ребята всё с большей неохотой относятся к учёбе, и в частности к математике. Многие ученики не знают даже таблицы умножения! Чтобы привлечь внимание учащихся к математике и ответить на вопрос «Надо ли знать таблицу умножения?» я выбрал тему проекта «Необычные способы умножения».
Вы не сможете выполнить умножения многозначных чисел — хотя бы даже двузначных — если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения.
В разное время разные народы владели разными способами умножения натуральных чисел.
Почему же сейчас все народы применяют один способ умножения «столбиком»?
Почему люди отказались от старых способов умножения в пользу современного?
Имеют ли забытые способы умножения право на существование в наше время?
Что бы ответить на эти вопросы я проделал следующую работу:
С помощью сети Интернета нашел информацию о некоторых способах умножения, которые использовались раньше.;
Изучил литературу, предложенную учителем;
Решил пару примеров всеми изученными способами, что бы узнать их недостатки;
4) Выявил среди них наиболее эффективные;
1 Умножение на 9 с помощью клеток тетради
Возьмём, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки.
Все очень просто!

2 Древнерусский способ умножения на пальцах
Это один из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы.
Принцип этого способа: умножение на пальцах однозначных чисел от 6 до 9. Пальцы рук здесь служили вспомогательным вычислительным устройством.
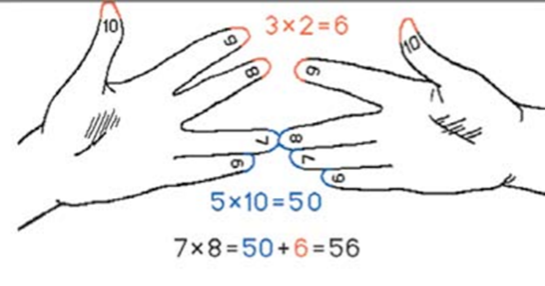
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел больше 5.
3 Крестьянский способ
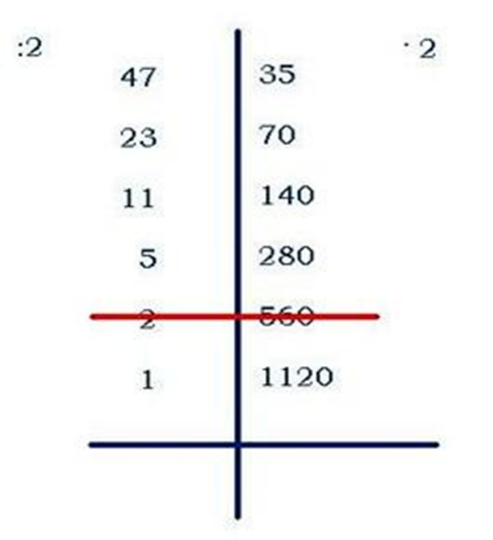
Это способ великорусских крестьян
Суть его заключается в том, что умножение любых чисел сводится к ряду последовательных делений одного числа пополам, при одновременном удвоении другого числа.
Для нечетных чисел.
4 Умножение графическим методом (линейным, китайским)
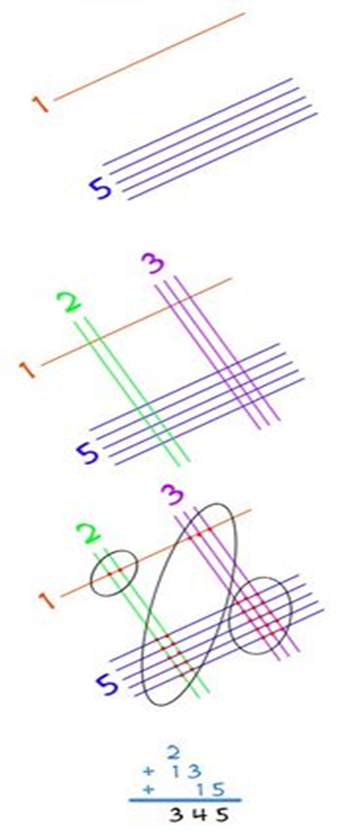
Перемножим два двузначных числа: 15*23
Шаг 1. первое число 15:
Рисуем первую цифру – одной линией.
Рисуем вторую цифру – пятью линиями.
Шаг 2. второе число 23:
Рисуем первую цифру – двумя линиями.
Рисуем вторую цифру – тремя линиями.
Шаг 3. Подсчитываем количество точек в группах.
Шаг 4. Результат – 345
5 Метод решетки. «Ревность»
Выдающийся арабский математик и астроном Абу Абдалах Мухаммед Бен Мусса аль-Хорезми жил и работал в Багдаде. В своей «Книге об индийском счете» ученый описал способ умножения, который назвали «Методом решетки».
Этот способ так же называют «Ревность».
Потому что получается картинка, похожая на витражное решетчатое окно венецианских домов, которое мешало уличным прохожим видеть сидящих у окон дам и монахинь.
3 4 7
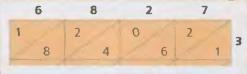
Умножаем, например, числа 6827 и 345:
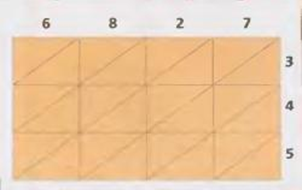
Вычерчиваем квадратную сетку и пишем один из номеров над колонками, а второй по высоте. В предложенном примере можно использовать одну из этих сеток.
2. Выбрав сетку, умножаем число каждого ряда последовательно на числа каждой колонки. В этом случае последовательно умножаем 3 на 6, на 8, на 2 и на 7. Посмотри на этой схеме, как пишется произведение в соответствующей клетке.
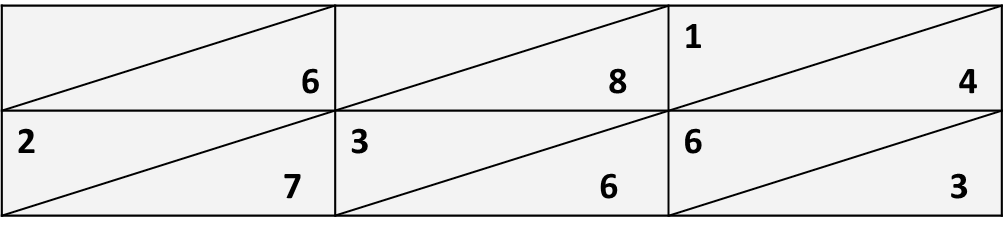
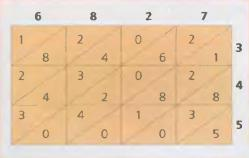
3. Посмотри, как выглядит сетка со всеми заполненными клетками.
4. В заключение складываем числа, следуя диагональным полосам. Если сумма одной диагонали содержит десятки, то прибавляем их к следующей диагонали.
Посмотри, как из результатов сложения цифр по диагоналям (они выделены жёлтым фоном) составляется число 2355315, которое и является произведение чисел 6827 и 345, то есть 6827 х 345 = 2355315.
С помощью секундомера установим сколько времени затрачивается на решение примера, каждым рассмотренным способом.
Источник