Проект необычные способы умножения многозначных чисел

Проект по математике на тему «Способы умножения чисел»

Научно практическая конференция школьников

« Необычные способы умножения»

Над проектом работал:

Карачев Ярослав ученик 5 а

класса МБОУ Лицея №81

Руководитель проекта: Вершинина Т.С.

Учитель математики МБОУ Лицея №81

Цель и задачи проекта:

Цель: ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.

Задачи: Найти и разобрать различные способы умножения.

Научиться демонстрировать некоторые способы умножения.

Рассказать о новых способах умножения и научить ими пользоваться учащихся.

Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.

Эксперимент «какой способ быстрей»

Гипотеза: Надо ли знать таблицу умножения?

Актуальность: В последнее время ребята всё с большей неохотой относятся к учёбе, и в частности к математике. Многие ученики не знают даже таблицы умножения! Чтобы привлечь внимание учащихся к математике и ответить на вопрос «Надо ли знать таблицу умножения?» я выбрал тему проекта «Необычные способы умножения».

Вы не сможете выполнить умножения многозначных чисел — хотя бы даже двузначных — если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения.

В разное время разные народы владели разными способами умножения натуральных чисел.

Почему же сейчас все народы применяют один способ умножения «столбиком»?

Почему люди отказались от старых способов умножения в пользу современного?

Имеют ли забытые способы умножения право на существование в наше время?

Что бы ответить на эти вопросы я проделал следующую работу:

С помощью сети Интернета нашел информацию о некоторых способах умножения, которые использовались раньше.;

Изучил литературу, предложенную учителем;

Решил пару примеров всеми изученными способами, что бы узнать их недостатки;

4) Выявил среди них наиболее эффективные;

1 Умножение на 9 с помощью клеток тетради

Возьмём, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки.

Все очень просто !

2 Древнерусский способ умножения на пальцах

Это один из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы.

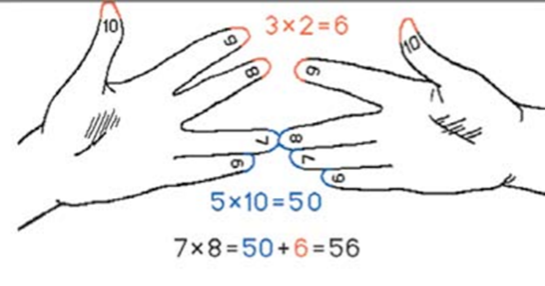
Принцип этого способа: умножение на пальцах однозначных чисел от 6 до 9. Пальцы рук здесь служили вспомогательным вычислительным устройством.

Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.

Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел больше 5.

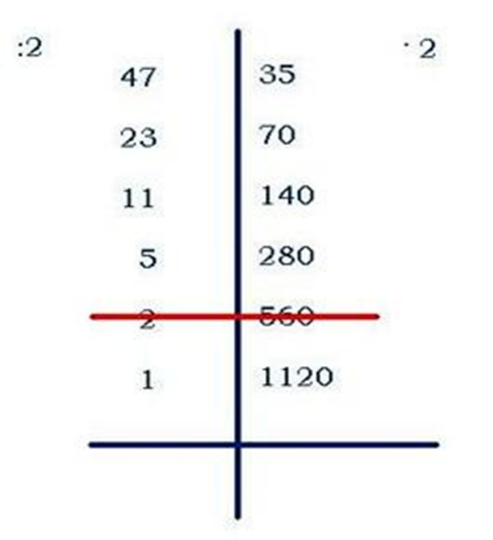
3 Крестьянский способ

Это способ великорусских крестьян

Суть его заключается в том, что умножение любых чисел сводится к ряду последовательных делений одного числа пополам, при одновременном удвоении другого числа.

Для нечетных чисел.

4 Умножение графическим методом (линейным, китайским)

Перемножим два двузначных числа: 15*23

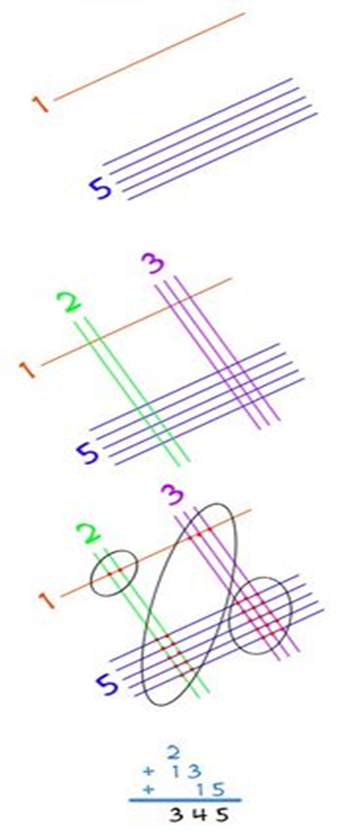
Шаг 1. первое число 15:

Рисуем первую цифру – одной линией.

Рисуем вторую цифру – пятью линиями.

Шаг 2. второе число 23:

Рисуем первую цифру – двумя линиями.

Рисуем вторую цифру – тремя линиями.

Шаг 3. Подсчитываем количество точек в группах.

Шаг 4. Результат – 345

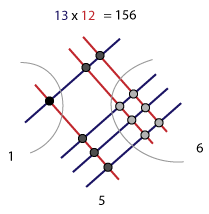
5 Метод решетки. «Ревность»

Выдающийся арабский математик и астроном Абу Абдалах Мухаммед Бен Мусса аль-Хорезми жил и работал в Багдаде. В своей «Книге об индийском счете» ученый описал способ умножения, который назвали «Методом решетки».

Этот способ так же называют «Ревность».

Потому что получается картинка, похожая на витражное решетчатое окно венецианских домов, которое мешало уличным прохожим видеть сидящих у окон дам и монахинь.

3 4 7

Умножаем, например, числа 6827 и 345:

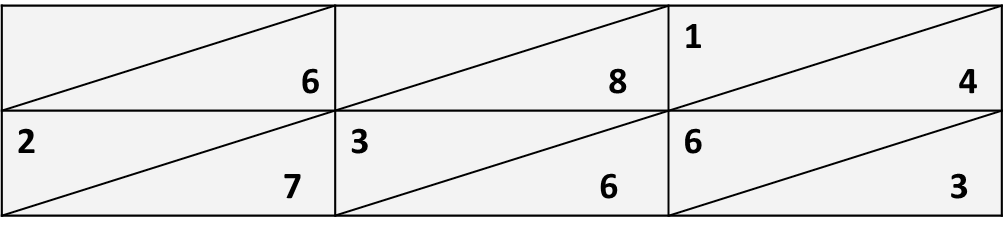
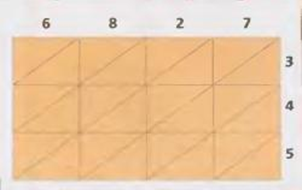
Вычерчиваем квадратную сетку и пишем один из номеров над колонками, а второй по высоте. В предложенном примере можно использовать одну из этих сеток.

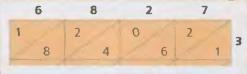
2. Выбрав сетку, умножаем число каждого ряда последовательно на числа каждой колонки. В этом случае последовательно умножаем 3 на 6, на 8, на 2 и на 7. Посмотри на этой схеме, как пишется произведение в соответствующей клетке.

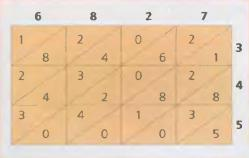
3. Посмотри, как выглядит сетка со всеми заполненными клетками.

4. В заключение складываем числа, следуя диагональным полосам. Если сумма одной диагонали содержит десятки, то прибавляем их к следующей диагонали.

Посмотри, как из результатов сложения цифр по диагоналям (они выделены жёлтым фоном) составляется число 2355315 , которое и является произведение чисел 6827 и 345, то есть 6827 х 345 = 2355315.

С помощью секундомера установим сколько времени затрачивается на решение примера, каждым рассмотренным способом.

Источник

Проект на тему: «Необычные способы умножения»

МБОУ «СОШ с. Вольное» Харабалинский район Астраханская область

« Необычные способы умножен ия »

ученики 5 класса :

Р уководитель проекта :

Вольное 201 6 год .

«Все есть число» Пифагор

В 21 веке невозможно представить себе жизнь человека, не производящего вычислений: это и продавцы, и бухгалтера, и обыкновенные школьники.

Изучение почти любого предмета в школе предполагает хорошие знания математики, и без нее нельзя освоить эти предметы. Две стихии господствуют в математике — числа и фигуры с их бесконечным многообразием свойств и действий с ними.

Нам захотелось больше узнать об истории возникновения математических действий. Сейчас, когда стремительно развивается вычислительная техника, многие не хотят утруждать себя счётом в уме. Поэтому мы решили показать не только то, что сам процесс выполнения действий может быть интересным, но и что, хорошо усвоив приёмы быстрого счёта, можно поспорить с ЭВМ.

Актуальность данной темы заключается в том, что использование нестандартных приёмов в формировании вычислительных навыков усиливает интерес учащихся к математике и содействует развитию математических способностей.

И зучить некоторые нестандартные приёмы умножения и показать, что их применение делает процесс вычисления рациональным и интересным и для вычисления которыми, достаточно устного счета или применения карандаша, ручки и бумаги.

Е сли наши предки умели умножать старинными способами, то если изучив по данной проблеме литературу, сможет ли современный школьник этому научиться, или нужны какие-то сверхъестественные способности.

1. Найти необычные способы умножения.

2. Научиться их применять.

3. Выбрать для себя самые интересные или более легкие, чем те которые предлагаются в школе, и использовать их при счете.

4. Научить одноклассников применять новы е способ ы умножения.

Объект исследования : математическое действие умножение

Предмет исследования : способы умножения

— поисковый метод с использованием научной и учебной литературы, интернета;

— исследовательский метод при определении способов умножения;

— практический метод при решении примеров;

— — анкетирование респондентов о знании нестандартных способов умножения.

Встречаются люди с необыкновенными способностями, которые по быстроте устных вычислений могут состязаться с ЭВМ. Их называют «чудо — счётчиками». И таких людей немало.

Рассказывают, что отец Гаусса, рассчитываясь со своими рабочими в конце недели, прибавлял оплату к каждому дневному заработку за сверхурочные часы. Однажды после того как Гаусс-отец закончил расчёты, следивший за операциями отца ребёнок, которому было 3 года, воскликнул: «Папа, подсчёт не верен! Вот такая должна быть сумма!» Вычисления повторили и с удивлением убедились, что мальчик указал правильную сумму.

В России в начале XX века блистал своими умениями «волшебник вычислений» Роман Семенович Левитан, известный под псевдонимом Арраго. Уникальные способности стали проявляться у мальчика уже в раннем возрасте. За несколько секунд он возводил в квадрат и куб десятизначные числа, извлекал корни разной степени. Казалось, всё это он делал с необычайной легкостью. Но эта легкость была обманчива и требовала большой работы мозга.

В 2007 году Марк Вишня, которому тогда было 2,5 года, поразил всю страну своими интеллектуальными способностями. Юный участник шоу «Минута славы» без труда считал в уме многозначные числа, опережая при вычислениях родителей и жюри, которые пользовались калькуляторами. Уже в два года он освоил таблицу косинусов и синусов, а также некоторые логарифмы.

В институте кибернетики Украинской академии наук проводились соревнования ЭВМ и человека. В соревновании участвовал молодой счётчик-феномен Игорь Шелушков и ЗВМ «Мир». Машина за несколько секунд сделала множество сложных операций, но победителем оказался Игорь Шелушков.

В Сиднейском университете в Индии тоже проходили соревнования человека и машины. Шакунтала Деви тоже опередила ЭВМ.

Большинство таких людей обладает прекрасной памятью и имеют дарование. Но некоторые из них никакими особыми способностями к математике не обладают. Они знают секрет! А секрет этот в том, что они усвоили приёмы быстрого счёта, запомнили несколько специальных формул. Значит, и мы тоже можем, пользуясь этими приёмами, быстро и точно считать.

Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И если бы школьник 21 века мог перенестись на пять веков назад, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.

Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия.

Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления — приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.

В книге В. Беллюстина «Как постепенно дошли люди до настоящей арифметики» изложено 27 способов умножения, причем автор замечает: «весьма возможно, что есть и еще способы, скрытые в тайниках книгохранилищ, разбросанные в многочисленных, главным образом, рукописных сборниках».

И все эти приемы умножения — «шахматный или органчиком», «загибанием», «крестиком», «решеткой», «задом наперед», «алмазом» и прочие соперничали друг с другом и усваивались с большим трудом.

Давайте рассмотрим наиболее интересные и простые способы умножения.

Источник

Проектная работа «Способы умножения чисел»

данная работа представляет собой проектную работу по математике.

Содержимое разработки

Научно практическая конференция школьников

« Необычные способы умножения»

Над проектом работал:

Ученик 5 В класса

Руководитель проекта: Трученкова Ю.В.

Учитель математики МОУ-СОШ №3

Цель и задачи проекта:

Цель: ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.

Задачи: Найти и разобрать различные способы умножения.

Научиться демонстрировать некоторые способы умножения.

Рассказать о новых способах умножения и научить ими пользоваться учащихся.

Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.

Эксперимент «какой способ быстрей»

Гипотеза: Надо ли знать таблицу умножения?

Актуальность: В последнее время ребята всё с большей неохотой относятся к учёбе, и в частности к математике. Многие ученики не знают даже таблицы умножения! Чтобы привлечь внимание учащихся к математике и ответить на вопрос «Надо ли знать таблицу умножения?» я выбрал тему проекта «Необычные способы умножения».

Вы не сможете выполнить умножения многозначных чисел — хотя бы даже двузначных — если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения.

В разное время разные народы владели разными способами умножения натуральных чисел.

Почему же сейчас все народы применяют один способ умножения «столбиком»?

Почему люди отказались от старых способов умножения в пользу современного?

Имеют ли забытые способы умножения право на существование в наше время?

Что бы ответить на эти вопросы я проделал следующую работу:

С помощью сети Интернета нашел информацию о некоторых способах умножения, которые использовались раньше.;

Изучил литературу, предложенную учителем;

Решил пару примеров всеми изученными способами, что бы узнать их недостатки;

4) Выявил среди них наиболее эффективные;

1 Умножение на 9 с помощью клеток тетради

Возьмём, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки.

Все очень просто!

2 Древнерусский способ умножения на пальцах

Это один из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы.

Принцип этого способа: умножение на пальцах однозначных чисел от 6 до 9. Пальцы рук здесь служили вспомогательным вычислительным устройством.

Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.

Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел больше 5.

3 Крестьянский способ

Это способ великорусских крестьян

Суть его заключается в том, что умножение любых чисел сводится к ряду последовательных делений одного числа пополам, при одновременном удвоении другого числа.

Для нечетных чисел.

4 Умножение графическим методом (линейным, китайским)

Перемножим два двузначных числа: 15*23

Шаг 1. первое число 15:

Рисуем первую цифру – одной линией.

Рисуем вторую цифру – пятью линиями.

Шаг 2. второе число 23:

Рисуем первую цифру – двумя линиями.

Рисуем вторую цифру – тремя линиями.

Шаг 3. Подсчитываем количество точек в группах.

Шаг 4. Результат – 345

5 Метод решетки. «Ревность»

Выдающийся арабский математик и астроном Абу Абдалах Мухаммед Бен Мусса аль-Хорезми жил и работал в Багдаде. В своей «Книге об индийском счете» ученый описал способ умножения, который назвали «Методом решетки».

Этот способ так же называют «Ревность».

Потому что получается картинка, похожая на витражное решетчатое окно венецианских домов, которое мешало уличным прохожим видеть сидящих у окон дам и монахинь.

3 4 7

Умножаем, например, числа 6827 и 345:

Вычерчиваем квадратную сетку и пишем один из номеров над колонками, а второй по высоте. В предложенном примере можно использовать одну из этих сеток.

2. Выбрав сетку, умножаем число каждого ряда последовательно на числа каждой колонки. В этом случае последовательно умножаем 3 на 6, на 8, на 2 и на 7. Посмотри на этой схеме, как пишется произведение в соответствующей клетке.

3. Посмотри, как выглядит сетка со всеми заполненными клетками.

4. В заключение складываем числа, следуя диагональным полосам. Если сумма одной диагонали содержит десятки, то прибавляем их к следующей диагонали.

Посмотри, как из результатов сложения цифр по диагоналям (они выделены жёлтым фоном) составляется число 2355315, которое и является произведение чисел 6827 и 345, то есть 6827 х 345 = 2355315.

С помощью секундомера установим сколько времени затрачивается на решение примера, каждым рассмотренным способом.

Источник