Проект графические способы умножения

Графический способ умножения

Исследовательский проект по математике НПК «Первые шаги в науку» школьный этап

Скачать:

Вложение	Размер
Графический способ умножения (презентация)	2.45 МБ
Графический способ умножения (доклад)	1.85 МБ

Предварительный просмотр:

Подписи к слайдам:

Графический способ умножения Выполнили: Блинова Алиса, Афанасьева Анна ученики 5 класса «А» Руководитель: Галайджян Андрей Сетракович , учитель математики МОУ СОШ № 28

Цель исследования: изучить графический способ умножения Задачи: изучить литературу по данной теме; провести анкетирование по теме исследования; научиться применять графический способ умножения; научить одноклассников использовать этот способ при вычислениях; апробировать графический способ умножения в 1А и 5А классах.

Вычислить 6 7 2

Пример 1. Вычислить

Пример 2. Вычислить

Апробация графического способа умножения в 1А классе .

Апробация графического способа умножения в 1А классе .

Апробация графического способа умножения в 1А классе .

Апробация графического способа умножения в 1А классе .

Апробация графического способа умножения в 1А классе .

Апробация графического способа умножения в 1А классе .

Апробация графического способа умножения в 1А классе .

Спасибо за внимание!

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

Павел Петрович Бажов. Хрупкая веточка

Чем пахнут ремёсла? Джанни Родари

Кто чем богат, тот тем и делится!

Астрономы получили первое изображение черной дыры

Источник

Графический способ умножения

Данная презентация расчитана на защиту учебного проекта по математике «Графический способ умножения»

Просмотр содержимого документа
«Графический способ умножения»

Выполнила: Снопок Дарья

ученица 5 класса

МАОУ НГО «СОШ № 12»

Руководитель: Жвакина Анастасия Михайловна

учитель МАОУ НГО «СОШ № 12»

• Изучить графический способ умножения чисел и его применение при вычислениях числовых выражений.

• Разобрать данный способ умножения.
• Рассказать о новом способе умножения и научить им пользоваться других.
• Развить навыки графического способа умножения.

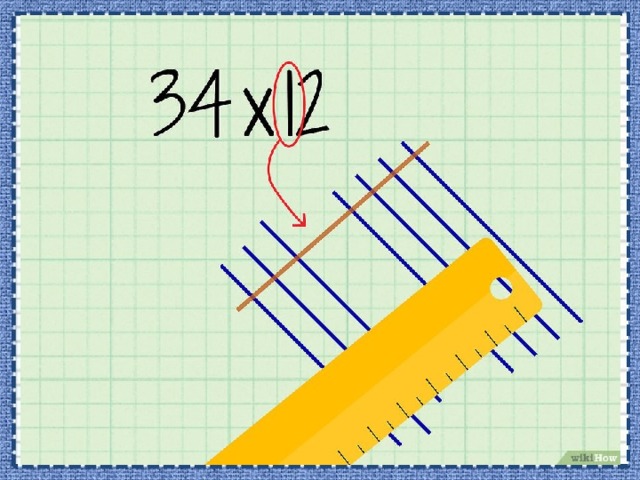
• Определите разряды цифр первого числа. Нужно определить количество разрядов и разряды каждой цифры.

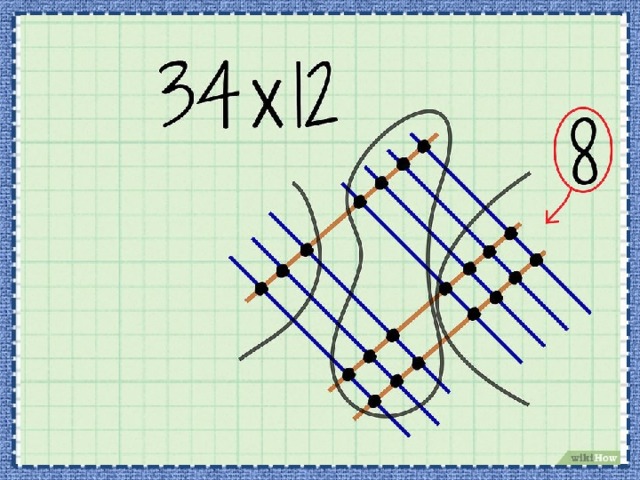
• Например, нужно перемножить . У числа 34 цифра 4 стоит в разряде единиц, а цифра 3 – в разряде десятков.

• Нарисуйте параллельные линии, представляющие разряд десятков первого числа. Количество линий соответствует цифре, которая стоит в разряде десятков.

• Нарисуйте наклонные линии (под углом в 45 градусов), которые убывают слева направо.

• Например, в случае числа 34 нарисуйте 3 параллельные линии.

• Нарисуйте параллельные линии, представляющие разряд единиц первого числа. Количество линий соответствует цифре, которая стоит в разряде единиц. Эти линии нарисуйте справа и выше линий, представляющих разряд десятков.

• Между линиями разряда десятков и линиями разряда единиц оставьте пустое пространство, чтобы отличать их.

• Например, в случае числа 34 нарисуйте 4 параллельные линии.

• Определите разряды цифр второго числа. Нужно определить количество разрядов и разряды каждой цифры.
• • В нашем примере у числа 12 цифра 2 стоит в разряде единиц, а цифра 1 – в разряде десятков.

• Нарисуйте параллельные линии, представляющие разряд десятков второго числа. Количество линий соответствует цифре, которая стоит в разряде десятков. Линии проведите в верхней части линий первого числа. Линии второго числа должны пересекать линии первого числа и возрастать справа налево.
• • Лучше нарисовать линии первого и второго чисел разными цветами.

• Например, в случае числа 12 нарисуйте 1 линию.

• Нарисуйте параллельные линии, представляющие разряд единиц второго числа. Количество линий соответствует цифре, которая стоит в разряде единиц. Эти линии нарисуйте справа и ниже линий, представляющих разряд десятков. Линии второго числа должны пересекать линии первого числа и возрастать справа налево.
• Между линиями разряда десятков и линиями разряда единиц оставьте пустое пространство, чтобы отличать их.
• Например, в случае числа 12 нарисуйте 2 параллельные линии.

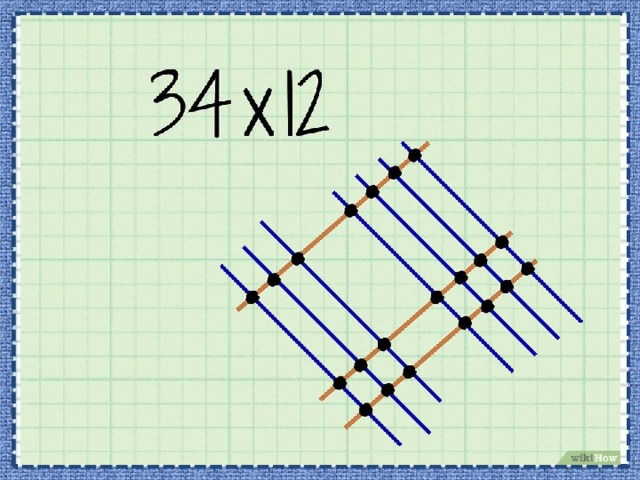
• Отметьте точки пересечений линий. Графический способ умножения подразумевает сложение точек, а не умножение чего-либо.

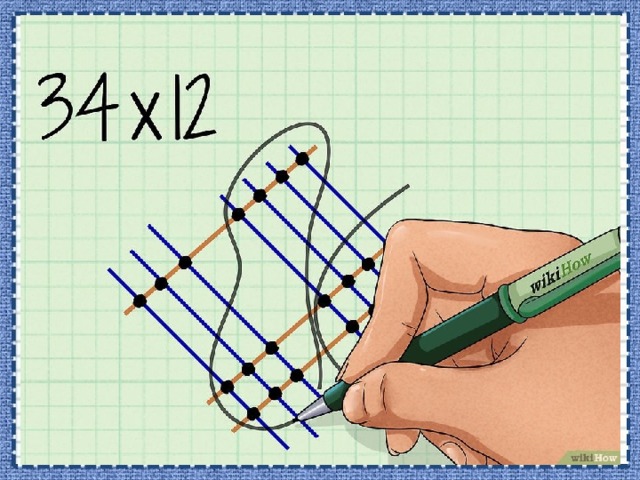
• Обведите точки, представляющие разряд единиц. Это точки пересечения линий разряда единиц первого и второго чисел.
• Вспомните, что 1 умножить на 1 равно 1.
• В нашем примере ( обведите точки пересечения четырех линий с двумя линиями (правая часть рисунка).

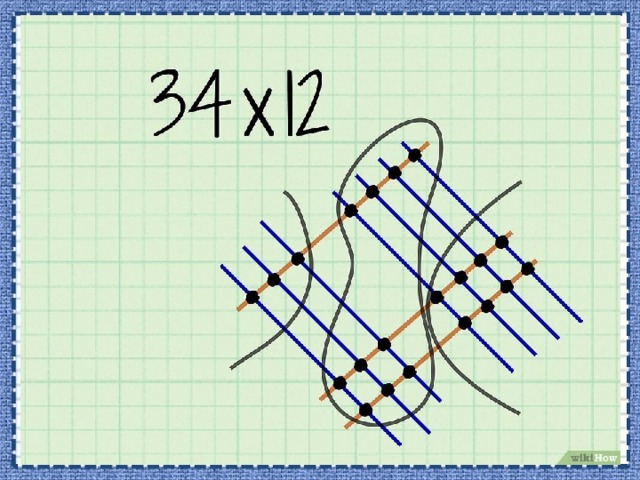
• Обведите точки, представляющие разряд десятков. Это точки пересечения линий разряда десятков (первого или второго числа) с линиями разряда единиц (первого или второго числа).
• Вспомните, что 1 умножить на 10 равно 10.
• В нашем примере обведите точки пересечения одной линии с четырьмя линиями (верхняя часть рисунка) и точки пересечения двух линий с тремя линиями (нижняя часть рисунка).

• Обведите точки, представляющие разряд сотен. Это точки пересечения линий разряда десятков первого и второго чисел.
• Вспомните, что 10 умножить на 10 равно 100.
• В нашем примере обведите точки пересечения трех линий с одной линией (левая часть рисунка).

• Сложите точки разряда единиц. Эти точки обведены в правой части рисунка. Полученную цифру запишите в разряд единиц конечного ответа.
• В нашем примере вы насчитаете 8 точек разряда единиц. Таким образом, 8 – это цифра, которая будет стоять в разряде единиц конечного числа.

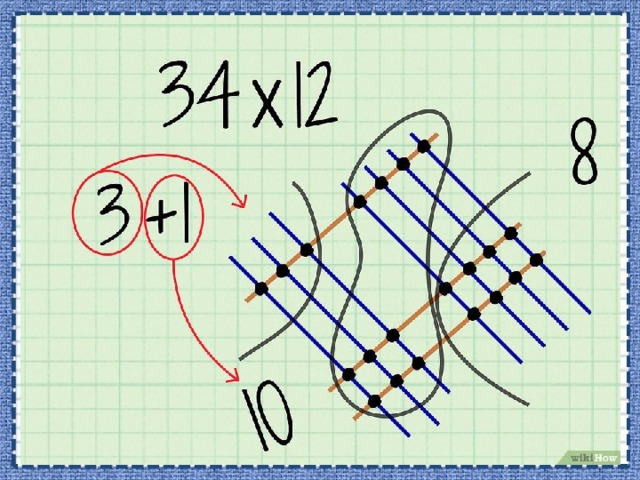
• Сложите точки разряда десятков. Эти точки обведены в верхней и нижней частях рисунка. Полученную цифру запишите в разряд десятков конечного ответа.
• В нашем примере вы насчитаете 10 точек разряда десятков.
• Вспомните, что если в операции сложения или умножения получилось двузначное число, применяется перенос цифр. Вы насчитали 10 точек; таким образом, 0 запишите в разряд десятков, а 1 перенесите в разряд сотен (конечного числа).

• Сложите точки разряда сотен. Эти точки обведены в левой части рисунка. Полученную цифру запишите в разряд сотен конечного ответа.
• В нашем примере вы насчитаете 3 точки разряда сотен.
• Не забудьте прибавить перенесенную цифру. В нашем примере из разряда десятков в разряд сотен перенесли 1, поэтому 3+1=4. Таким образом, запишите 4 в разряд сотен конечного числа.

• Запишите окончательный ответ. Запишите цифры (рядом друг с другом), найденные для каждого разряда.
• В нашем примере вы нашли, что цифра 8 должна стоять в разряде единиц, цифра 0 – в разряде десятков, цифра 4 – в разряде сотен. Таким образом, окончательный ответ: 408.

Источник

Презентация проектной работы на тему «Графические способы умножения»

Описание презентации по отдельным слайдам:

Проектная работа Графические способы умножения. Выполнила Хохлова Евгения, учащаяся 5 класса А. Руководитель Хохлова Г.В., учитель математики.

Цели: Познакомиться со старинными приемами умножения. Расширить знания по различным приемам умножения. Научиться выполнять действия с натуральными числами, используя старинные способы умножения.

Задачи: Найти и разобрать различные способы умножения. Научиться демонстрировать некоторые способы умножения. Рассказать о новых способах умножения и научиться ими пользоваться. Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.

Объект исследования: арифметическое действие «умножение». Предмет исследования: различные нестандартные способы умножения. Гипотеза исследования: использование нестандартных приемов в формировании вычислительных навыков умножения усиливает интерес учащихся к математике и содействует развитию математических способностей.

Этапы исследования: — сбор материала о способах умножения чисел; — систематизация и обобщение результатов исследования; — вывод. Методы исследования: — поисковый; — описательный; — метод анализа и обобщения.

История появления таблицы умножения. При раскопках здания в городе Нара, древней столице Японии, археологами была найдена деревянная табличка с фрагментом таблицы умножения. Из всех табличек, обнаруженных в Японии, найденная – самая древняя.

Хотя не исключено, что система устного счета появилась независимо в разных местах. Узнать имя гениального математика, который первым додумался записать результаты умножения в виде таблицы, скорее всего, не удастся. Это пришло в голову сразу нескольким людям. Но в европейской культуре автором таблицы умножения считается знаменитый греческий математик Пифагор.

Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и сложными приемами. Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу одновременно была чуть ли не дюжина различных способов.

Приемы были один другого запутаннее. Человек средних способностей не мог запомнить их все. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия.

За тысячелетия развития математики было придумано множество способов умножения Давайте рассмотрим наиболее интересные и простые способы умножения.

Умножение «на пальцах». Вот, например, как умножали древние римляне на пальцах числа от 6 до 10. 1. Мысленно пронумеруем свои пальцы от 6 до 10 на каждой руке, начиная с мизинца. Пусть требуется умножить 7 на 8. 2. Кончик пальца 7 левой руки касается кончика пальца 8 правой руки. Соприкасающиеся пальцы и все пальцы ниже считают десятками. У нас это 50. 3. Теперь верхние пальцы левой и правой руки перемножаются друг с другом. Слева у нас 3, а справа 2. 3·2=6 4. Теперь складываем оба числа: 50+6=56. Правильно?

Умножение на 9. Допустим, нам надо умножить 3 на 9. Чтобы вычислить ответ, надо найти палец под номером 3 и загнуть его. Количество пальцев слева от загнутого пальца – это десятки, количество пальцев справа – это единицы. У нас слева – 2 пальца, это 2 десятка, а справа 7 пальцев. Значит, 3·9=27.

Крестьянский способ умножения или метод «удвоения и раздвоения». Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.

Способ «Решетка» (итальянский). В предложенном примере можно использовать такого вида сетку. Умножаем число каждого ряда последовательно на числа каждой колонки. В этом случае последовательно умножаем 9 на 7, на 9, и на 3. В заключение складываем числа, следуя диагональным полосам. Начинаем складывать справа налево. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали. Так пишется каждое произведение в соответствующей клетке. Число 72956 является ответом.

Китайский или японский способ. Цель этого счета заключается в том, чтобы, не зная таблицы умножения можно без ошибок посчитать большие числа. Всё решается по алгоритму, который быстро и легко запоминается. Всё очень просто — рисуются наклонные линии, по количеству десятков и единиц. Первый множитель рисуется с левым уклоном, второй с правым, десятки левее, единицы правее. Затем отделяем самые левые пересечения, самые правые, и остаётся середина. Считаем количество точек на пересечениях и просто записываем результат, сотни (самая левая группа точек), десятки (серединные точки) и единицы (группа точек справа). В принципе, метод можно применять и для трёхзначных чисел и для более крупных чисел. Главное правильно выделять группы чисел и обращать внимание на перенос.

Заключение. Научившись считать всеми представленными способами, я пришла к выводу: самые простые способы это те, которые мы изучаем в школе. Возможно они просто для нас более привычны.

Спасибо за внимание!

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 829 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 296 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 607 человек из 76 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-479305

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В российских школах оборудуют кабинеты для сообщества «Большой перемены»

Время чтения: 1 минута

В Пензенской области запустят проект по снижению административной нагрузки на учителей

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Минпросвещения работает над единым подходом к профилактике девиантного поведения детей

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник