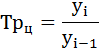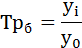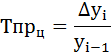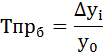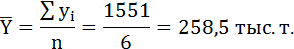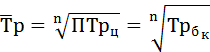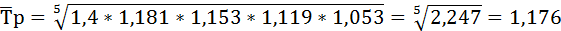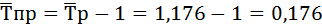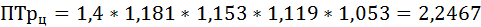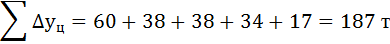Проанализировать динамику цепным способом

Статистика: Учебник / Под ред. Елисеевой.- М., 2006. С. 168-172

Оглавление

Показатели динамики (цепные и базисные)

Показатели динамики нашли широкое применения для формирования более наглядного представления о тенденции изменения уровней динамического ряда. Рост и снижение уровня ряда могут происходить либо равномерно, либо ускоренно, либо замедленно. Аналитические возможности показателей динамики раскрывает следующий фрагмент из учебника «Статистика»:

«Уровни временного ряда могут изменяться в самых разных, направлениях: они могут возрастать или убывать, повторять ранее достигнутый уровень. Интенсивность их изменения бывает различной. Уровни ряда могут изменяться быстрее или медленнее. Для характеристики развития явления во времени применяются следующие показатели:

• абсолютные приросты (_у);
• темпы роста (Т_р);
• темпы прироста (снижения) (Т_р);
• абсолютное ускорение или замедление ();
• относительное ускорение (Т_р).

Абсолютный прирост (абсолютное изменение) уровней ряда рассчи­тывается как разность двух уровней. Он показывает, на сколько единиц уровень одного периода больше или меньше уровня другого периода.

В зависимости от базы сравнения абсолютные приросты могут быть цепными и базисными:

Если каждый последующий уровень ряда динамики сравнивается со своим предыдущим уровнем, то прирост называется цепным. Если же в качестве базы сравнения выступает за ряд лет один и тот же период, то прирост называется базисным.

Один и тот же по величине абсолютный прирост может означать разную интенсивность изменения уровней (см. табл. 9.4).

Абсолютные приросты, тыс. шт.

Темпы роста, %

Темпы прироста, %

цепные

базисные

цепные

базисные

базисные

В нашем примере в 1996 и 1998 гг. абсолютное изменение объема продукции было одинаковым — 5 тыс. шт., но интенсивность рос­та объема произведенной продукции в эти годы была различной: в 1996 г. прирост в 5 тыс. ед. по сравнению с предыдущим годом составил 25%, а в 1998 г. по сравнению с предыдущим годом — лишь 14,3%. Аналогично один и тот же прирост в 10 тыс. ед. для 1997 и 1999 гг. означает разную интенсивность роста: в 1997 г. — прирост составил по сравнению с предыдущим годом, 40%, а в 1999 г. – 25%.

Интенсивность изменения уровней временного ряда характеризуется темпами роста и прироста.

Темп роста есть отношение двух уровней ряда. Как и абсолютные приросты, темпы роста могут рассчитываться как цепные и как базисные:

Если база сравнения по периодам меняется, то найденные темпы роста называются цепными. Если же база сравнения по периодам неизменна (y₀), то темпы роста называются базисными.

Темпы роста, выраженные в коэффициентах, принято называть коэффициентами роста:

В анализе используется один из этих показателей: либо темп роста, либо коэффициент роста, ибо экономическое их содержание одно и то же, но по-разному выражено: в % (Т_р) и в разах (К_р). Так по данным табл. 9.4 можно сделать вывод, что наибольшая интенсивность роста была достигнута в 1997 г., когда темп роста составил 140%, или в 1,4 раза превысил уровень предыдущего года.

Если цепные темпы роста характеризуют интенсивность изменения уровней от года к году (от месяца к месяцу), то базисные темпы роста фиксируют интенсивность роста, (снижения) за весь интервал времени между текущим и базисным уровнями. Так в примере базисный темп роста за весь период с 1996 по 1999 г. составил 250% (1995 г. взят за базу сравнения).

Темп прироста есть отношение абсолютного прироста к предыдущему уровню динамического ряда (цепной показатель) и к уровню, принятому за базу сравнения по динамическому ряду (базисный показатель):

По данным табл. 9.4, темп прироста для 1999 г. составит: цепной — 25% (·100) и базисный – 150% (·100), т.е. в 1999 г. объем продукции увеличился по сравнению с 1998 г. на 25%, а в целом за весь рассматриваемый период прирост составил 150%.

Между цепными и базисными показателями изменения уровней ряда существует следующая взаимосвязь:

• сумма цепных абсолютных приростов равна базисному приросту (см. табл. 9.4, где в итоговой строке накопленный прирост за 1996 — 1999 гг. – 30 тыс. шт. – совпадает с базисным абсолютным приростом для 1999 г.);
• произведение цепных коэффициентов роста равно базисному или равносильное этому деление рядом стоящих базисных коэффициентов роста друг на друга равно цепным коэффициентам роста. Так, по данным табл. 9.4, имеем:

, или 250% – базисный темп роста;

200/175=1,143, или 114,3% – цепной коэффициент роста для 1998 г. Взаимосвязь цепных и базисных темпов (коэффициентов) роста позволяет при анализе, если необходимо, переходить от цепных показателей к базисным и наоборот;

• темп прироста связан с темпом роста: (см. табл. 9.4, где темпы прироста меньше темпов роста на 100). Поэтому при анализе обычно приводится какой-то один из них: темп роста либо темп прироста. Зная цепные темпы прироста, можно определить базисный темп прироста. Для этого нужно от темпов прироста перейти к темпам (коэффициентам) роста и далее воспользоваться указанной выше взаимосвязью коэффициентов роста.

Так, например, изменение цен на потребительские товары и услуги за I квартал 2001 г. оказалось в Санкт-Петербурге следующим (см. гл. 9.5).

Изменение цен (в % к предыдущему месяцу)

В целом за I квартал прирост цен составит:

, т.е. в марте 2001 г. по сравнению с декабрем 2000 г. цены выросли на 7,4%.

Чтобы знать, что скрывается за каждым процентом прироста, рассчитывается абсолютное значение 1% прироста как отношение абсолютного прироста уровня за интервал времени к темпу прироста за тот же промежуток времени:

или

Иными словами, абсолютное значение 1% прироста в данном периоде есть сотая часть достигнутого уровня в предыдущем периоде (см. табл. 9.4, последнюю графу). В связи с этим расчет абсолютного значения 1% прироста базисным методом не имеет смысла, ибо для каждого периода это будет одна и та же величина – сотая часть уровня базисного периода.

Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. Если они систематически возрастают, то ряд развивается с ускорением. Величина абсолютного ускорения определяется как т.е. по аналогии с цепным абсолютным приростом, но сравниваются между собой не уровни ряда, а их скорости. По табл. 9.4 в нашем примере ускорение имело место лишь в 1997 и в 1999 гг., когда =10-5=5 тыс. шт.

Если систематически растут цепные темпы роста, то ряд развивается с относительным ускорением. Относительное ускорение можно определить как разность следующих друг за другом темпов роста или прироста:

или

Полученная величина выражается в процентных пунктах (п.п.). По данным табл. 9.4, относительное ускорение имело место лишь в 1997 г.– 15 процентных пунктов по сравнению с предыдущим годом.

Относительное ускорение может быть измерено и с помощью коэффициента опережения.

Коэффициент опережения определяется как отношение последующего темпа роста к предыдущему:

В нашем примере коэффициент опережения для 1997 г. составил:

140/125=1,12, что означает, что в 1997 г. темп роста был в 1,12 раза больше, чем в 1996 г.

Коэффициенты опережения принято рассчитывать в сравнительном анализе нескольких рядов динамики. При параллельном изучении нескольких рядов динамики обычно их приводят к одному основанию путем расчета базисных темпов роста с одинаковой по времени базой сравнения для всех рядов. Это позволяет наглядно видеть, для какого ряда интенсивность изменения уровней наибольшая. Сравнивая далее наибольшие темпы роста с наименьшими, определяют коэффициенты опережения в развитии одного явления по отношению к другому (табл. 9.6).

Динамика доходов предприятия за 1-е полугодие 2004 г.(тыс. руб.)

Месяцы

Прибыль от реализации продукции

Прибыль от продажи прочих актов

Источник

Задача №56. Расчёт аналитических показателей динамики

Добыча нефти характеризуется следующими данными:

Годы	Произведено продукция, тыс. шт.	Абсолютное значении 1 % прироста, тыс. шт.

Годы	Добыча нефти, тыс. т
1-ый	150
2-ой	210
3-ий	248
4-ый	286
5-ый	320
6-ой	337

Произвести анализ ряда динамики по:

1) показателям, характеризующим рост добычи нефти (на цепной и базисной основе): абсолютный прирост, темпы роста и прироста (по годам к базисному году); результаты расчетов изложить в табличной форме;

2) средний уровень и среднегодовой темп ряда динамики;

3) показать взаимосвязь между цепными и базисными показателями.

Решение:

Абсолютный прирост цепной (Δy_ц) – это разность между текущим уровнем ряда и предыдущим:

Так, во 2-ом г. прирост добычи нефти в сравнении с первым годом составит:

= 210 – 150 = 60 тыс. т.

В 3-ем году прирост добычи нефти в сравнении со 2-м годом составит:

Δy_{ц 3-й год} = 248 – 210 = 38 тыс. т.

Аналогично исчисляются абсолютные приросты за последующие годы. Результаты расчётов занесём в таблицу.

Абсолютный прирост базисный (Δy_б) – это разность между текущим уровнем ряда и уровнем ряда, выбранным за базу сравнения:

Так как в задании не указано, какой год взять в качестве базисного года, по умолчанию будем считать базисным 1-й год.

Абсолютный прирост базисный во 2-ом г. совпадает с цепным абсолютным приростом в этом году:

Δy_б = 210 – 150 = 60 тыс. т

в 3-ем году базисный абсолютный прирост равен:

Δy_б = y₃ – y₂ = 248 – 150 = 98 тыс. т и т.д (гр. 3 расчётной таблицы).

Темп роста (Тр) – отношение уровней ряда динамики, которое выражается в коэффициентах и процентах.

Цепной темп роста исчисляют отношением текущего уровня к предыдущему:

(гр. 5 расчётной таблицы);

базисный – отношением каждого последующего уровня к одному и тому же уровню, принятому за базу сравнения:

(гр. 4 расчётной таблицы).

Темп прироста (Тпр) так же может быть цепной или базисный.

Цепной рассчитывается как отношение абсолютного прироста к предыдущему уровню ряда динамики:

Базисный темп прироста рассчитывается как отношение абсолютного прироста к базисному уровню ряда динамики:

Если предварительно был вычислен темп роста, то темп прироста можно рассчитать как разность между темпами роста и единицей, если темпы роста выражены в коэффициентах:

или как разность между темпами роста и 100%, если темпы роста выражены в процентах:

Тпр= Тр – 100% (гр. 6 и 7 расчётной таблицы).

Годы	Добыча нефти, тыс. т	Абсолютный прирост базисный, тыс. т	Абсолютный прирост цепной, тыс. т	Темп роста базисный, %	Темп роста цепной, %	Темп прироста базисный, %	Темп прироста цепной, %
А	1	2	3	4	5	6	7
1-ый	150	0	—	100,00	—	—	—
2-ой	210	60	60	140,00	140,0	40,00	40,0
3-ий	248	98	38	165,33	118,1	65,33	18,1
4-ый	286	136	38	190,67	115,3	90,67	15,3
5-ый	320	170	34	213,33	111,9	113,33	11,9
6-ой	337	187	17	224,67	105,3	124,67	5,3

Из таблицы видно, что добыча нефти росла от года к году. Однако прирост добычи с каждым годом становился меньше.

2) Средний уровень ряда определяется в данном случае по формуле средней арифметической простой, где в числителе сумма уровней динамического ряда, а в знаменателе их число:

Среднегодовой темп роста ряда динамики рассчитывается по формуле средней геометрической

где ПТр – произведение цепных темпов роста (в коэффициентах),

– конечный базисный темп роста (в коэффициентах),

n – число темпов.

Среднегодовой темп прироста ряда динамики:

Добыча нефти ежегодно возрастала в среднем на 17,6%.

3) Между цепными и базисными темпами роста имеется взаимосвязь:

произведение цепных темпов роста (в коэффициентах) равно конечному базисному темпу роста.

Сумма цепных абсолютных приростов равна конечному базисному абсолютному приросту:

Выводы: С 1 по 6 годы добыча нефти росла от года к году. Объём добычи нефти за эти годы вырос на 124,7%, что в абсолютном выражении составило 187 т. Однако ежегодный прирост добычи с каждым годом снижался. В среднем добыча нефти ежегодно возрастала на 17,6%.

Источник