Принцип якорного способа управления исполнительными двигателями

Принцип якорного способа управления исполнительными двигателями

Несмотря на ряд существенных недостатков, связанных с наличием скользящего контакта между щеткой и коллектором, исполнительные двигатели постоянного тока широко используются в системах автоматического управления, регулирования и контроля, поскольку обладают и рядом положительных качеств, в частности такими как: плавное, широкое и экономичное регулирование частоты вращения; практическое отсутствие ограничений на максимальную и минимальную частоту вращения; большие пусковые моменты; хорошая линейность механических а при якорном управлении и регулировочных характеристик.

Как и любые исполнительные двигатели, эти имеют две обмотки: обмотку возбуждения и обмотку управления. При этом напряжение управления может подаваться либо на обмотку якоря, либо на обмотку возбуждения. Поэтому различают якорное и полюсное управление.

§ 2.1 Якорное управление исполнительным двигателем

Рис. 2.1. Схема включения исполнительного двигателя при якорном управлении

Схема включения двигателя с якорным управлением показана на рис. 2.1. Напряжение возбуждения подается на обмотку полюсов, напряжение управления — на обмотку якоря. Коэффициент сигнала a здесь равен a = U_у/U_в. Для двигателей с постоянными магнитами a = U_у/U_у.ном. Регулирование частоты вращения осуществляется изменением напряжения управления.

При отсутствии насыщения Ф_в= k_фU_в, а поскольку U_в = const, магнитный поток возбуждения также остается постоянным, т.е. Ф_в = const.

Вращающий момент двигателя

Выразим момент в относительных единицах, приняв за базовый момент пусковой момент, развиваемый двигателем при n = 0 и a = 1

Тогда относительное значение момента m = M/M_б

(2.1)

Частота вращения при холостом ходе (m = 0 и a = 1)

(2.2)

Откуда находим c_еk_ф= 1/n_о. Подставляя это значение в (2.1), получим

(2.3)

где n = n/n_о— относительная частота вращения двигателя.

(2.4)

Уравнение (2.3) есть уравнение механической характеристики исполнительного двигателя при якорном управлении. Решив его относительно n, получим уравнение регулировочной характеристики

Механическая мощность в относительных единицах р_мх = mn = n(a — n). Угловую скорость, при которой наступает максимум мощности, найдем известным приемом (dp_мх/dn = 0), откуда n_м= a/2, а максимальное значение механической мощности будет

Мощность управления

Приняв за базовую единицу мощность управления при коротком замыкании Р_у.к (n = О, a = 1)

получим мощность управления в относительных единицах

На рис. 2.2,а представлены механические, на рис. 2.2,б — регулировочные характеристики, а на рис. 2.3 показана зависимость р_мх = f(n) исполнительного двигателя. Проанализируем свойства двигателя при якорном способе управления.

Механические характеристикилинейные и параллельные, что означает независимость быстродействия от коэффициента сигнала. Пусковой момент и угловая скорость холостого хода пропорциональны коэффициенту сигнала.

Рис.2.2. Механические (а) и регулировочные (б) характеристики исполнительного двигателя постоянного тока при якорном управлении

Рис. 2.3. Зависимость механической мощности от скорости вращения при якорном управлении

Регулировочные характеристикилинейные. Напряжение трогания пропорционально моменту нагрузки. Линейность механических и регулировочных характеристик является важным достоинством якорного управления.

Мощность управления резко возрастает с увеличением коэффициента сигнала. Кроме того, она доходит до 95 % полной потребляемой мощности двигателя, поскольку является мощностью якорной цепи, что характерно для двигателей постоянного тока.

В данном случае это является существенным недостатком якорного управления, ибо предполагает наличие мощных и дорогих усилителей.

Мощность возбуждения остается величиной постоянной, независящей ни от коэффициента сигнала, ни от частоты вращения. К тому же — она небольшая по величине, что также характерно для машин постоянного тока.

Максимум механической мощности в сильной степени зависит от коэффициента сигнала и даже при a = 1 не превышает 1/4 базовой мощности.

§ 2.3. Полюсное управление исполнительным двигателем

Рис. 2.4. Схема включения исполнительного двигателя при полюсном управлении

Схема управления приведена на рис.2.4 Напряжение управления подается на обмотку главных полюсов, напряжение возбуждения — на обмотку якоря, по которой в течение всего времени работы двигателя протекает ток возбуждения. В двигателях, мощностью более 10 Вт, для его ограничения включают дополнительное сопротивление R_д.

Если пренебречь насыщением магнитной цепь, можно считать Ф = k_фU_у = k_фaU_в. Тогда ток якоря

Принимая за базовый момент пусковой (n = 0, a =1))

получим относительное значение момента

С учетом (2.2) уравнение механической характеристики примет вид

Решив его относительно n, получим уравнение регулировочной характеристики

Механическая мощность в относительных единицах р_мх= mn = an — a 2 n 2 . Скорость, при которой наступает максимум мощности n_м = 0,5/a. Тогда максимальная механическая мощность будет

Мощность возбуждения р_в = U_вI_в. Подставляя значение тока, получим

На рис. 2.5,а представлены механические, на рис. 2.5,б — регулировочные характеристики, а на рис. 2.6 показана зависимость р_мх = f(n) исполнительного двигателя при полюсном управлении.

Рис.2.5. Механические (а) и регулировочные (б) характеристики исполнительного двигателя постоянного тока при полюсном управлении

Проанализируем эти графики.

Механические характеристики линейные, но непараллельные, к тому же и неоднозначные (одну и ту же частоту вращения можно получить при разных значениях a). Пусковой момент прямо-, а частота вращения холостого хода обратно пропорциональны коэффициенту сигнала и при малых a может существенно превышать номинальную, что безусловно опасно для двигателя.

Регулировочные характеристикинелинейные, а при m 0,5.

Мощность управления пропорциональна квадрату коэффициента сигнала и не зависит от частоты вращения. Она значительно меньше, чем при якорном управлении, что является достоинством данного способа.

Мощность возбужденияс увеличением частоты вращения уменьшается и тем быстрее, чем больше a.

Максимум механической мощности не зависит от коэффициента сигнала, что также можно отнести к достоинствам полюсного управления.

Несмотря на отмеченные достоинства полюсного управления, предпочтение все-таки следует отдать якорному потому, что оно обеспечивает линейные и однозначные характеристики, в принципе исключает самоход (при полюсном он возможен из-за взаимодействия тока якоря с потоком остаточной намагниченности полюсов), обладает более высоким быстродействием, поскольку индуктивность якоря меньше индуктивности обмотки возбуждения.

Источник

Исполнительный двигатель с якорным управлением

У исполнительных двигателей с якорным управлением обмоткой возбуждения является обмотка полюсов, а обмоткой управления— обмотка якоря (см. рис. 1.2, а). На все время работы автоматического устройства обмотку возбуждения подключают сети с постоянным напряжением U_B. На обмотку управления подают сигнал U_y — напряжение управления — лишь тогда, когда необходимо вращение якоря двигателя. От величины напряжения управления зависит величина вращающего момента и частота вращения двигателя. При изменении полярности напряжения управления меняется направление вращения якоря двигателя.

Так как при работе двигателя напряжение возбуждения U_B постоянно, то ток в обмотке возбуждения I_в, а следовательно, и магнитный поток Ф_в также постоянны (Ф_в ≡ I_в ≡U_B):

(1.1)

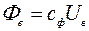
При вращении якоря в обмотке якоря (управления) наводится противо-ЭДС Е_у, величина которой пропорциональна потоку Ф_в и частоте вращения п:

Ток якоря (обмотки управления) определяется согласно выражению:

, (1.2)

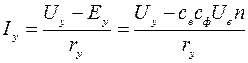
где r_у —сопротивление обмотки якоря (управления).

Вращающий момент двигателя развивается за счет взаимодействия потока возбуждения Ф_в с током якоря I_у:

(1.3)

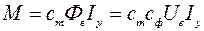
После подстановки I_у из выражения (1.2) получим

(1.4)

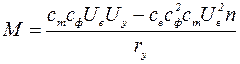
Для того чтобы характеристикам двигателей придать универсальный характер, независимый от мощности двигателя и его конструктивных особенностей, при анализе исполнительных двигателей здесь и в дальнейшем будем пользоваться системой относительных единиц, т. е. выражать действительные величины (момент, мощность, частоту вращения, напряжение управления и т. п.) через отношения их к некоторым постоянным величинам, принятым за единичные.

За напряжение управления U_y в относительных единицах α примем его отношение к постоянному по величине напряжению возбуждения:

(1.5)

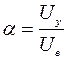
Назовем α коэффициентом сигнала.

Заменив в выражении момента (1.4) U_y через U_Bα, получим

(1.6)

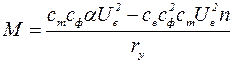
За единицу момента в относительных единицах примем момент М_пуск1, развиваемый двигателем при пуске (n=0), когда коэффициент сигнала α=1, т. e.U_y=U_B.

Согласно (1.6) величина этого момента

(1.7)

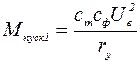
Единичный момент М_пуск1 для любого двигателя является вполне определенной постоянной величиной.

Выражение момента двигателя в относительных единицах найдем как отношение действительного момента М к единичному М_пуск1:

(1.8)

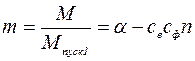
За единицу частоты вращения в относительных единицах примем частоту вращения при идеальном холостом ходе n₀₁ (при m=0) в случае равенства напряжений управления и возбуждения (U_у=U_в).

Выражение единичной частоты вращения найдем из уравнения (1.8) путем подстановки в него m=0 и α=1:

(1.9)

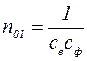
Частота вращения n₀₁ — постоянная, вполне определенная для любого двигателя величина.

Заменим в выражении момента (1.8) с_ес_ф на :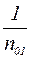

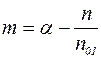
, (1.10)

Преобразуя полученное уравнение и учитывая, что отношении действительной частоты вращения n к единичной n₀₁ есть частота вращения в относительных единицах ν, получим уравнение механической характеристики двигателя:

Это уравнение показывает, что вращающий момент m исполнительного двигателя с якорным управлением является линейной функцией частоты вращения ν и коэффициента сигнала α.

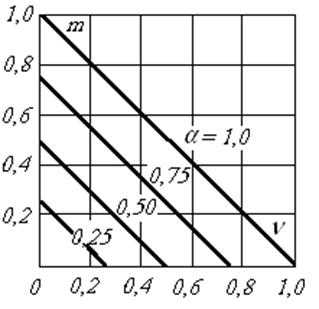
На рис. 1.3 представлено семейство механических характеристик двигателя m = f(v) при α=const, построенных в относительных единицах на основании уравнения (1.11), где α=0,25; 0,50; 0,75; 1,0.

Рис. 1.3 Механические характеристики при якорном управлении

Из уравнения (1.11) и рис. 1.3 следует, что при заданном постоянном коэффициенте сигнала (напряжении управления) частота вращения двигателя уменьшается с увеличением момента на валу по линейному закону.

Максимальный момент двигателя имеет место при пуске (при v=0). Величина максимального (пускового) момента в относительных единицах равна коэффициенту сигнала (при v = 0; m=α), т. е. пусковой момент пропорционален напряжению управления: М_пуск1≡U_y. Последнее означает, что напряжение трогания U_тр (напряжение, при котором якорь двигателя при заданном моменте сопротивления на валу начинает вращаться) прямо пропорционально моменту сопротивления. При уменьшении напряжения управления (коэффициента сигнала) механические xapaктеристики двигателя смещаются (параллельно) в сторону меньших частот и моментов. Жесткость (наклон) механических характеристик при этом не изменяется.

Частота вращения при холостом ходе двигателя v₀ (при m=0) в относительных единицах, как это следует из уравнения (1.11), равна коэффициенту сигнала α, т. е. пропорциональна напряжению управления (n₀=U_y).

Если выражение (1.11) переписать в виде

то оно будет являтьсяуравнением регулировочной характеристики двигателя с якорным управлением: ν=f(α) при m=const.

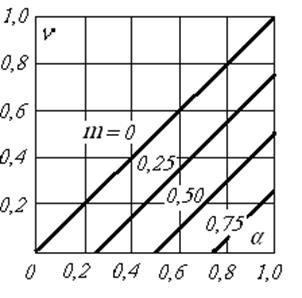
На рис. 1.4 изображено семейство регулировочных характеристик, построенных в относительных единицах для m = 0; 0,25; 0,50; 0,75.

Рис. 1.4. Регулировочные характеристики при якорном управлении

Из этих характеристик, а также из выражения (1.12) следует, что при любом заданном моменте сопротивления на валу частота вращения двигателя v возрастает с увеличением напряжения управления U_y (коэффициента сигнала α) по линейному закону. Иными словами, частота вращения пропорциональна напряжению управления: n≡U_у.

Максимальная частота вращения, которую развивает двигатель при определенном моменте сопротивления на валу, имеет место при номинальном напряжении управления (при α=1). Эта частота обратно пропорциональна моменту сопротивления m.

Весьма ценным свойством исполнительных двигателей постоянного тока с якорным управлением является линейность их механических и регулировочных характеристик. Этим свойством не обладает ни один другой исполнительный двигатель.

Мощность возбуждения исполнительного двигателя с якорным управлением равна электрическим потерям в активном сопротивлении r_в обмотки возбуждения:

(1.13)

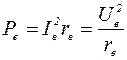
Эта мощность при постоянном напряжении возбуждения U_в (что имеет место в реальных двигателях) постоянна — она не зависит от нагрузки. Ее величина, как и величина потерь в обмотках возбуждения любого двигателя постоянного тока, незначительна, поскольку основная часть потребляемой двигателем мощности идет через якорь.

Мощность возбуждения, выраженная в процентном отношении к полной мощности, потребляемой двигателем, растет с уменьшением номинальной мощности двигателя: от 5% (в двигателях с номинальной механической мощностью 250 Вт) до 30% (в двигателях с мощностью 5÷7 Вт).

Мощность управления двигателя постоянного тока c 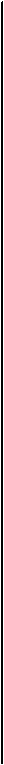якорным управлением равна произведению напряжения U_у на ток I_у (ток якоря):

Эта мощность равна сумме полной механической мощности развиваемой двигателем (включая потери на трение в подшипниках, о воздух), и потерь в якоре (электрические — в обмотке магнитные — в стали). Это, по существу, вся мощность, потребляемая двигателем, за исключением потерь в обмотке возбуждения Р_в. Мощность управления достаточно велика, что является большим недостатком двигателей постоянного тока с якорным управлением, так как в случае питания обмотки управления от усилителя приходится значительно увеличивать габариты его, следовательно, и автоматического устройства в целом.

При постоянном моменте на валу, что чаще всего бывает на практике, вследствие постоянства потока Ф_в ток управления [см. (1.3)] постоянен и мощность управления [см. (1.14)] пропорциональна напряжению управления U_y (коэффициенту сигнала α).

Механическая мощность на валу двигателя (Р₂=Мω или в относительных единицах p₂=mv) при заданном напряжении управления (коэффициенте сигнала α) является нелинейной функцией частоты вращения:

При пуске (v=0) и холостом ходе (m=0) она равна нулю и достигает максимума при частоте вращения, равной половине частоты вращения холостого хода v₀=α, т. е. при v_p2max= 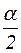, в чем можно убедиться, продифференцировав зависимость (1.15) по v и приравняв производную нулю.

Максимум механической мощности р_2max может быть найден путем подстановки v_p2max в выражение (1.15):

р_2mах= 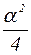, (1.16)

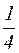
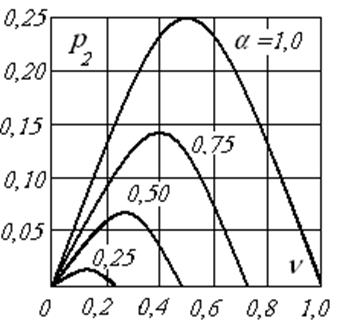
т. е. максимальная механическая мощность двигателя пропорциональна квадрату коэффициента сигнала (напряжения управления). При номинальном напряжении управления (α=1) р_2mах составляет от мощности, потребляемой якорем двигателя при пуске, когда n=0 и U_y=U_в (эта мощность принимается за единичную).

На рис. 1.5 представлено семейство кривых p₂=f(ν) при α=const, где α=0,25; 0,50; 0,75; 1,0.

Рис. 1.5 Зависимость механической мощности от частоты вращения при якорном управлении

К исполнительным двигателям постоянного тока с якорным управлением, кроме двигателей с обмоткой возбуждения на полюсах, относятся также двигатели с постоянными магнитами. У этих двигателей обмотка возбуждения отсутствует, основной магнитный поток создается постоянными магнитами.

По своим рабочим и регулировочным свойствам двигатели постоянными магнитами практически не отличаются от двигателей с якорным управлением: они имеют такие же механические и регулировочные характеристики, такие же зависимости p₂=f(ν).

Преимущество двигателей с постоянными магнитами — у них нет обмотки возбуждения, они имеют более высокий КПД из-за отсутствия потерь на возбуждение, их магнитный поток практически не зависит от изменений температуры окружающей среды (чего нельзя сказать об обычных двигателях).

Недостатки двигателей с постоянными магнитами — старение магнитов, которое особенно интенсивно происходит в условиях тряски и вибраций, что приводит к уменьшению магнитного потока и к изменению свойств двигателей; стоимость двигателей с постоянными магнитами, несмотря на кажущуюся -их простоту, не меньше, а иногда даже больше стоимости двигателей с обмоткой возбуждения. Причинами этого являются высокая стоимость и сложность обработки магнитотвердых материалов, идущих для изготовления постоянных магнитов. Именно поэтому до недавнего времени с постоянными магнитами выпускались лишь микродвигатели мощностью до 10÷15 Вт. Наибольшее распространение получили микродвигатели серии ДПМ.

В’ последние годы появились и получили довольно широкое промышленное распространение дешевые легко обрабатываемые ферритно-бариевые магниты. Они позволили создать сравнительно недорогие исполнительные двигатели постоянного тока больших мощностей — 10 кВт и более. Это так называемые высокомоментные двигатели, применение которых дает значительный экономический и технический эффект, особенно в станкостроительной промышленности.

Источник