Пример алгебраического способа задачи

Решение задач алгебраическим методом
методическая разработка по алгебре (5 класс)

Знакомство с алгебраическим методом решения текстовых задач

Скачать:

Вложение	Размер
reshenie_tekstovyh_zadach_algebraicheskim_metodo1.docx	26.38 КБ
reshenie_tekstovyh_zadach_algebraicheskim_metodo1.docx	26.38 КБ

Предварительный просмотр:

РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ АЛГЕБРАИЧЕСКИМ МЕТОДОМ

Лиханова В.Е., учитель математики МБОУ «СОШ №12» г. Ноябрьск, ЯНАО

Наряду с арифметическим, практическим методами решения задач ученики 5 класса знакомятся и с алгебраическим методом. Многие ученики сначала не будут принимать новый метод, поэтому роль учителя на данном этапе должна заключаться в том, чтобы показать преимущества данного метода, но ни в коем случае не навязывать его. С этой целью необходимо предлагать задачи, которые арифметически решить трудно.

Особенностями алгебраического метода является введение переменной величины, что позволяет действовать с ней как с явной. Выполняется анализ основных зависимостей между явными и неявными значениями величин, производится моделирование условия задачи в виде уравнения. Если при выборе действий опираемся на сюжетные особенности, то такой метод решения называется алгебраическим. Следует отметить, что в учебнике «Математика 5» авторского коллектива: Г.В.Дорофеев, И.Ф. Шарыгин, Е.А. Бунимович, Л.В. Кузнецова существуют определенные недостатки по обучению решению задач алгебраическим методом. Самым главным из них является недостаточность системы упражнений, готовящих детей к усвоению данного метода, а именно на составление различных выражений по сюжету задач и выяснение их сюжетного смысла.

Необходимые базовые знания для решения задач алгебраическим методом:

• усвоение понятия переменной величины;
• умение решать простые и составные уравнения;
• умение составлять по тексту задачи простые и составные выражения и определять их сюжетный смысл;
• находить выражения с одинаковым сюжетным смыслом.

Основные этапы формирования умения решать задачи алгебраическим методом:

1. Подготовительный.
2. Этап ознакомления с алгоритмом рассуждения и записью решения задачи.
3. Закрепление, выработка умения.

На первом этапе учитель должен познакомить учащихся с понятием «сюжетный смысл выражения», научить составлять всевозможные выражения по тексту задачи, определять их сюжетный смысл. Это можно сделать через следующую систему упражнений:

1. Дать текст с числами. Составить по этому тексту несколько выражений, записать их смысл.
2. Дать текст. Учитель составляет по этому тексту выражения, а ученики объясняют их смысл по тексту.
3. Предложить задание, подобное предыдущему, но среди выражений должны быть такие, которые не имеют сюжетного смысла по данному тексту.
4. По предложенному тексту с числами дети сами составляют выражения и определяют их смысл. В заключение находят выражения с одинаковым сюжетным смыслом.
5. Дать задачу, показать способ обозначения величины, которую требуется найти в вопросе задачи через х, показать способ составления выражений по задаче с использованием этой неизвестной величины как с известной. Определить сюжетный смысл выражений по тексту задачи.
6. По предложенному тексту учитель показывает сюжетный смысл одного из выражений. Детям предлагается составить выражение с тем же сюжетным смыслом.

У пруда росли липы, осины, березы и ели. Лип росло 12, осин – в 3 раза больше, чем лип, несколько елей, берез – на 5 меньше, чем елей. Составь различные выражения и объясни, что они обозначают.

Учитель предлагает обозначить число елей буквой х , работать с ней как с обыкновенным числом. Можно составить следующие выражения:

12·3 – количество осин,

х-5 – количество берез,

12+х – количество лип и елей,

12+(х-5) – количество лип и берез,

12·3+(х-5)+х –общее количество осин, берез, елей.

Основная задача второго этапа – введение понятия «основание для составления уравнения», введение алгоритма рассуждения и развернутой формы записи решения задачи алгебраическим методом. Деятельность учителя может быть организована следующим образом.

1. Дать текст задачи. Решить ее арифметическим методом.
2. Предложить обозначить через х неизвестную величину, значение которой требуется найти.
3. Составить ряд выражений по тексту и определить их сюжетный смысл.
4. Найти выражения с одинаковым сюжетным смыслом. Сообщить детям, что если выражения имеют одинаковый смысл, то они равны.
5. Составить равенство из двух выражений, в одно из которых входит переменная.
6. Вместе с детьми определить, что данная запись является уравнением.
7. Решить его и установить, что значение х и есть ответ.
8. Сообщить учащимся, что сюжетный смысл выражений, которые мы использовали для составления уравнения, будем называть основанием для составления уравнения, а метод решения задачи – алгебраическим.
9. Решить еще одну задачу таким же методом. Запомнить алгоритм рассуждений и полную форму записи решения задачи.
10. Решив другую задачу, учитель предлагает проверить правильность решения задачи. Для этого необходимо вспомнить все известные способы проверки правильности решения, которые использовали ранее.
11. Сообщить детям новый способ проверки. Для этого надо составить уравнение по другому основанию. Сделать вывод.
12. Сопоставляя решения первой и второй задачи, учитель в процессе фронтальной беседы составляет алгоритм решения задачи алгебраическим методом.

Алгоритм решения задачи алгебраическим методом.

1. Обозначить буквой неизвестную величину.
2. Составить выражения.
3. Выбрать основание.
4. Составить уравнение.
5. Решить уравнение.

6. Проверить правильность решения.

Знакомство с новым методом решения задачи можно начать:

• с простой задачи;
• сразу с составной.

В первом случае работа будет выполняться достаточно быстро, но учащиеся не увидят преимущества данного метода (ведь задача и так решена !).

Рассмотрим задачу. Ученики изготовили 135 елочных украшений, из них фонариков на 5 больше, чем хлопушек, а снежинок в 3 раза больше, чем снежинок. Сколько хлопушек изготовили дети?

Необходимо показать, что задача решается с помощью уравнения. Для этого надо ввести переменную величину. Обозначить буквой можно как число хлопушек, так и число фонариков, так и число снежинок (проще — число хлопушек). Составляем выражения с переменной.

Хлопушки- ? штук

Фонарики-?, на 5 штук больше 135 штук

Снежинки-?, в 3 раза больше

Пусть х штук хлопушек сделали дети, тогда они изготовили (х+5) штук фонариков, 3х штук снежинок. Всего было сделано (х+(х+5)+3х) штук украшений , а это – 135 штук украшений. Выражения ( х+(х+5)+3х ) и 135 имеют один и тот же сюжетный смысл, значит, их можно приравнять. Требуется подчеркнуть, чту уравнивать можно только выражения, имеющие одинаковый сюжетный смысл. Получится уравнение:

х+(х+5)+3х=135. Обратить внимание, что в уравнении наименования не пишутся. Решим уравнение

Итак, 26 хлопушек сделали дети.

Предложить решить задачу арифметическим методом . Без вспомогательной модели это сделать трудно. Составим схематический чертеж.

Хл.

Ф. 5 ш. 135 ш.

Сн. .

Все украшения можно разделить на 5 равных частей, если бы не было5 штук фонариков. Уберем их, при этом общее количество уменьшится на 5.

1) 135-5=130 (шт.) — украшений всего.

1. 130:5=26 (шт.) – в одной части , т.е. столько хлопушек сделали дети.

В задачах с пропорциональными величинами желательно использовать таблицу не только для краткой записи содержания, но и для проведения рассуждений при составлении уравнения. Сначала в таблице записывается содержание задачи, а затем (желательно другим цветом) заполняются все пустые графы выражениями с переменной величиной.

Из двух городов, расстояние между которыми 1620 км вышли одновременно навстречу друг другу два поезда, скорость одного на 10 км/ч больше скорости другого и через 18 часов они встретились. Какова скорость каждого поезда?

Скорость

Расстояние

(х+10)км/ч На 10 км/ч больше

Источник

Решение задач алгебраическим способом

Презентация к уроку математики в 5 классе «Решение задач алгебраическим способом» по учебнику И.И.Зубаревой. Цели презентации:
— показать правило решения задач алгебраическим способом;
— формировать умение решать задачи арифметическим и алгебраическим способами.

На примерах решения задач № 509 и № 510 из учебника «Математика. 5 класс» И.И.Зубаревой рассматриваются арифметический и алгебраический способы решения. При использовании данной презентации на уроке учитель может предложить учащимся самостоятельно найти разные способы решения задач и затем дополнить их способы новым способом – алгебраическим. С помощью специальных гиперссылок в презентации учащимся можно демонстрировать варианты записи решения задач.

Просмотр содержимого документа
«Решение задач алгебраическим способом»

Решение задач алгебраическим способом (с помощью уравнений) По учебнику И.И. Зубаревой, А.Г. Мордковича

Автор работы : Белякова Ольга Владимировна,

учитель математики МОУ «ЛСОШ №2»

г. Лихославль Тверской области

Цели: — показать правило решения задач алгебраическим способом; — формировать умение решать задачи арифметическим и алгебраическим способами.

Арифметический (решение задачи по действиям)

Алгебраический (решение задачи с помощью уравнения)

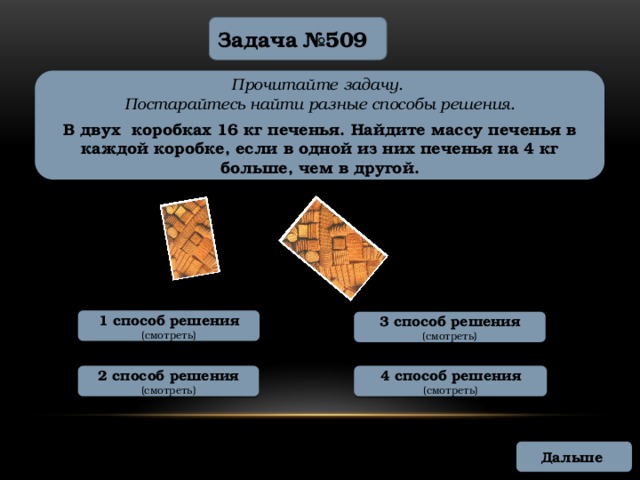
Постарайтесь найти разные способы решения.

В двух коробках 16 кг печенья. Найдите массу печенья в каждой коробке, если в одной из них печенья на 4 кг больше, чем в другой.

1 способ решения

3 способ решения

2 способ решения

4 способ решения

1 способ (арифметический)

• 16 – 4 = 12 (кг) – печенья останется в двух коробках, если из первой коробки достать 4 кг печенья.

• 12 : 2 = 6 (кг) – печенья было во второй коробке.

• 6 + 4 = 10 (кг) – печенья было в первой коробке.

Ответ : масса печенья в первой коробке – 10 кг, а во второй 6 кг.

В решении использован способ уравнивания .

Вопрос : почему он получил такое название?

2 способ (арифметический)

• 16 + 4 = 20 (кг) – печенья станет в двух коробках, если во вторую коробку добавить 4 кг печенья.

• 20 : 2 = 10 (кг) – печенья было в первой коробке.

• 10 — 4 = 6 (кг) – печенья было во второй коробке.

Ответ : масса печенья в первой коробке – 10 кг, а во второй 6 кг.

В решении использован способ уравнивания .

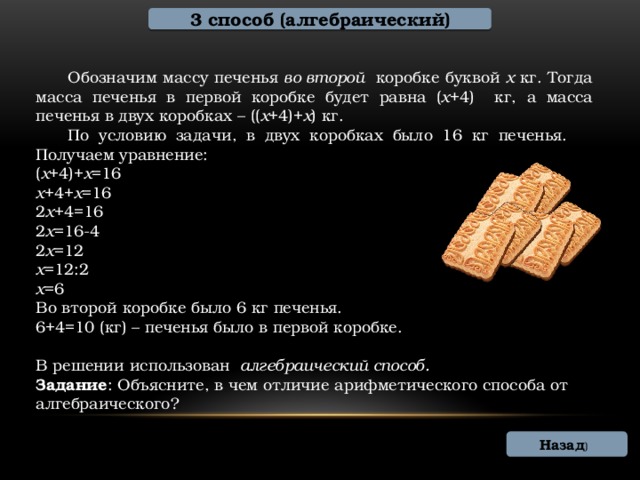
3 способ (алгебраический)

Обозначим массу печенья во второй коробке буквой х кг. Тогда масса печенья в первой коробке будет равна ( х +4) кг, а масса печенья в двух коробках – (( х +4)+ х ) кг.

По условию задачи, в двух коробках было 16 кг печенья. Получаем уравнение:

Во второй коробке было 6 кг печенья.

6+4=10 (кг) – печенья было в первой коробке.

В решении использован алгебраический способ.

Задание : Объясните, в чем отличие арифметического способа от алгебраического?

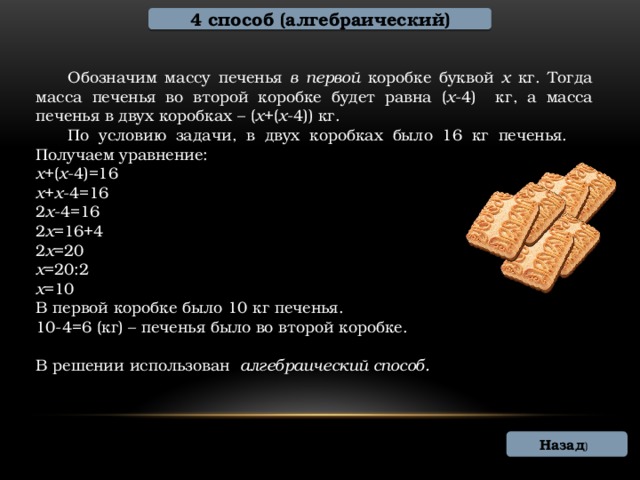
4 способ (алгебраический)

Обозначим массу печенья в первой коробке буквой х кг. Тогда масса печенья во второй коробке будет равна ( х -4) кг, а масса печенья в двух коробках – ( х +( х -4)) кг.

По условию задачи, в двух коробках было 16 кг печенья. Получаем уравнение:

В первой коробке было 10 кг печенья.

10-4=6 (кг) – печенья было во второй коробке.

В решении использован алгебраический способ.

• Какие два способа решения задачи были использованы?
• Что собой представляет способ уравнивания?
• Чем первый способ уравнивания отличается от второго?
• В одном кармане на 10 рублей больше, чем в другом. Как можно уравнять количество денег в обоих карманах?
• В чем заключается алгебраический способ решения задачи?
• Чем отличается 3 способ решения задачи от 4-го?
• В одном кармане на 10 рублей больше, чем в другом. Известно, что меньшее количество денег обозначили переменной х . Как будет выражаться через х количество денег в другом кармане?
• Если за х обозначить большее количество денег в кармане, тогда как будет выражаться через х количество денег в другом кармане?
• В магазине шампунь стоит на 25 руб дороже, чем в супермаркете. Обозначьте одну переменную буквой у и выразите другую стоимость через эту переменную.

Решите задачу арифметическим и алгебраическим способами.

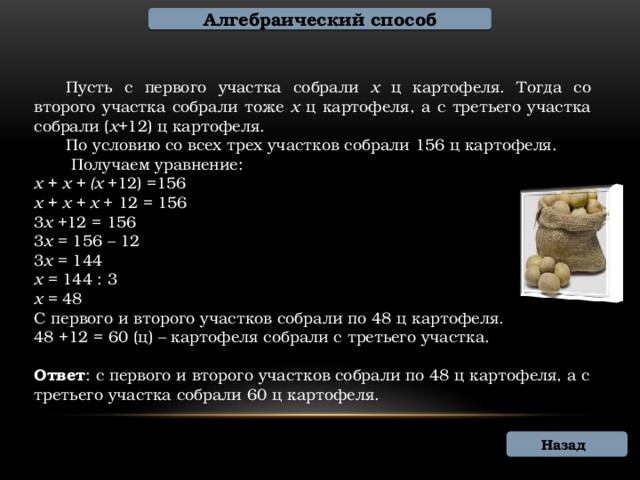
С трех участков земли собрали 156 ц картофеля. С первого и второго участков картофеля собрали поровну, а с третьего – на 12 ц больше, чем с каждого из двух первых. Сколько картофеля собрали с каждого участка.

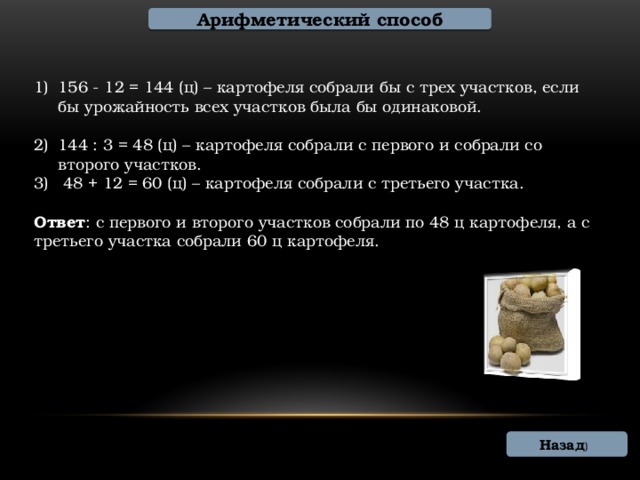
• 156 — 12 = 144 (ц) – картофеля собрали бы с трех участков, если бы урожайность всех участков была бы одинаковой.

• 144 : 3 = 48 (ц) – картофеля собрали с первого и собрали со второго участков.
• 48 + 12 = 60 (ц) – картофеля собрали с третьего участка.

Ответ : с первого и второго участков собрали по 48 ц картофеля, а с третьего участка собрали 60 ц картофеля.

Пусть с первого участка собрали х ц картофеля. Тогда со второго участка собрали тоже х ц картофеля, а с третьего участка собрали ( х +12) ц картофеля.

По условию со всех трех участков собрали 156 ц картофеля.

х + х + х + 12 = 156

С первого и второго участков собрали по 48 ц картофеля.

48 +12 = 60 (ц) – картофеля собрали с третьего участка.

Ответ : с первого и второго участков собрали по 48 ц картофеля, а с третьего участка собрали 60 ц картофеля.

Источник