Применяя способ преобразования чертежа высоту пирамиды

Способы преобразования чертежа: Способ замены плоскостей проекций, Способы вращения: Методические рекомендации для самостоятельной работы студентов , страница 2

Часто для приведения прямой, плоской фигуры или пространственной формы в то частное положение, которое требуется для решения задачи, приходится заменять обе плоскости проекций. Переход от заданной системы плоскостей V/H к новой V₁/H₁ может быть осуществлен по одной из приведенных ниже схем:

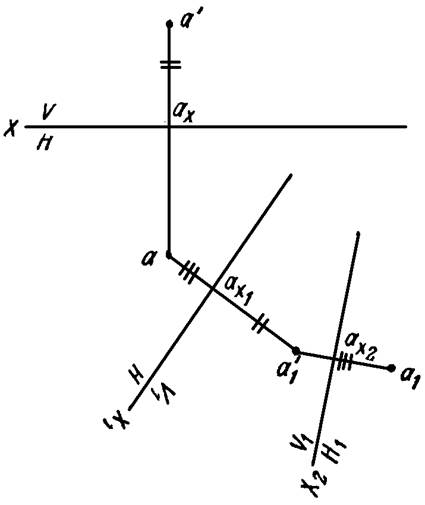
На рисунке 12 задана точка A в системе V/H. Затем осуществлен переход от системы V/H к системе V₁/H₁: проведена новая ось проекций Х₁, найдена новая проекция а’₁ точки А. Далее система V₁/H заменена новой системой плоскостей проекции V₁/H₁ —вместо горизонтальной плоскости проекций введена новая плоскость Н₁.

Положение новых осей проекций выбирается в соответствии с конкретными условиями задачи.

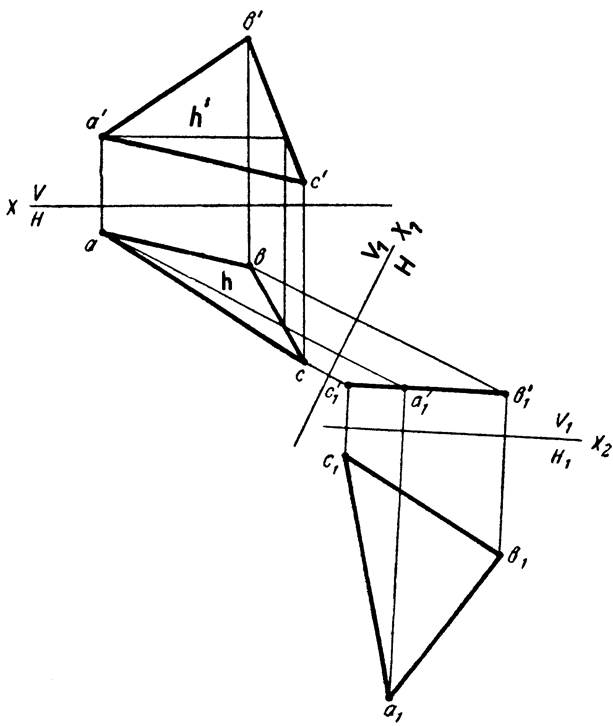
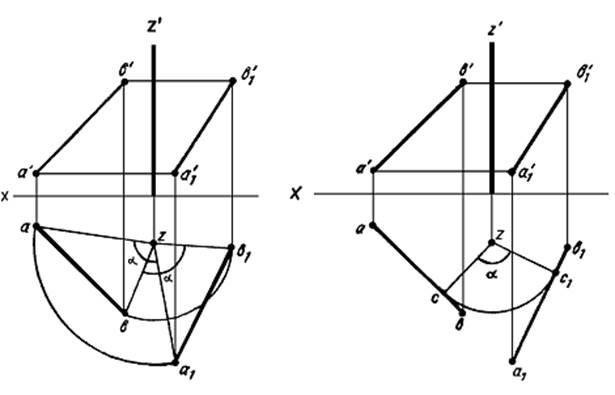
Пример 6. Определить истинную фигуру треугольника ABC (рисунок 13).

Треугольник спроектируется в натуральную величину на какую-либо плоскость проекций, если он окажется параллельным этой плоскости. Для того чтобы треугольник АВС оказался параллельным одной из плоскостей проекций, необходимо выполнить двойную замену плоскостей.

Сначала заменим плоскость V на плоскость V₁. Плоскость V₁ выберем перпендикулярно плоскости треугольника АВС — новая ось проекций x₁должна быть перпендикулярна горизонтальной проекции горизонтали h. На новую фронтальную плоскость проекций треугольник cпроектируетcя в виде прямой линии c’₁a’₁b’₁. Затем введем новую плоскость проекций H₁ параллельно плоскости треугольника.

Горизонтальная проекция a₁b₁c₁ треугольника ABC в новой системе — истинная величина его.

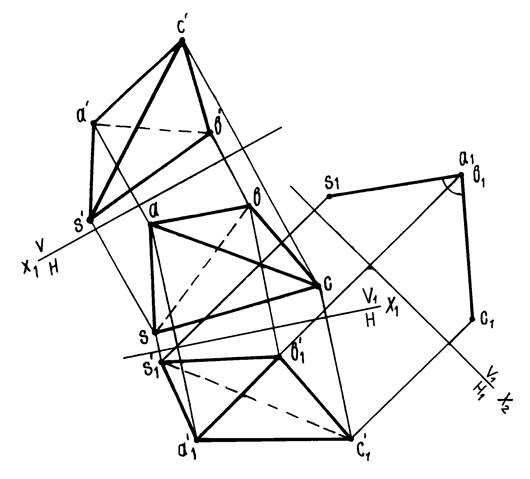
Пример 7. Дана пирамида SАВС (рисунок 14). Определить величину двугранного угла при ребре АВ.

Задача сводится к построению проекции данного угла на плоскость проекций, перпендикулярную к его ребру.

Так как ребро АВ — прямая общего положения, то необходимо произвести две последовательные замены плоскостей проекций. Плоскость V заменяем плоскостью V₁, параллельной отрезку АВ.

Находим новую фронтальную проекцию s’₁a’₁b’₁c’₁ пирамиды SАВС на новой фронтальной плоскости проекций. Затем от системы V₁/H перейдем к системе V₁/H₁. Плоскость H₁ расположим перпендикулярно отрезку АВ. На плоскость Н₁ ребро АВ спроектируется в точку, а грани SАВ и САВ — в прямые. Угол s₁a₁c₁ будет искомым.

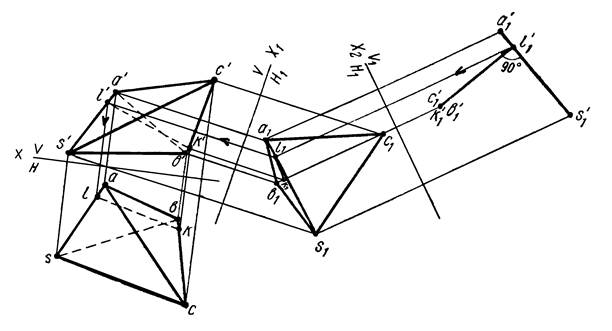
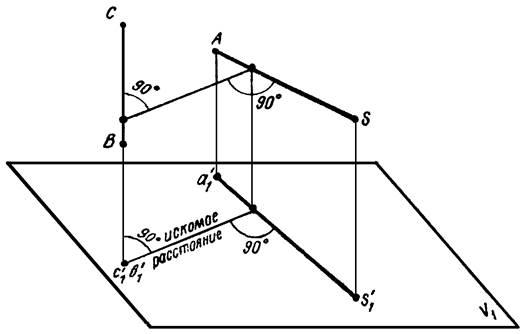
Пример 8. Дана пирамида SАВС (рисунок 15). Определить кратчайшее расстояние между ребрами SА и ВС.

Прямые SА и ВС являются скрещивающимися. Следовательно, задача сводится к определению кратчайшего расстояния между двумя скрещивающимися прямыми. Для решения задачи необходимо произвести такую замену плоскостей проекций, чтобы в новой системе одна из прямых, например ВС (рисунок 16), оказалась перпендикулярной к какой-либо плоскости проекций. Замену плоскостей проекций осуществляем по схеме V/H → V/H₁ → V₁/H₁.

Следовательно, решение задач методами преобразования сводится к выполнению четырех основных этапов:

1) преобразование прямой общего положения в прямую уровня (определение углов наклона прямой к плоскостям проекций и натуральной величины отрезков);

2. преобразование прямой уровня в проецирующую прямую (определение величины двугранного угла, расстояния между прямыми);

3. преобразование плоскости общего положения в проецирующую плоскость (определение углов наклона плоскости к плоскостям проекций, расстояния от точки до плоскости);

4. преобразование плоскости проецирующей в плоскость уровня (определяется натуральная величина плоскости).

В системе V₁H₁ прямая ВС (см. рисунок 15) проектируется в точку. Отрезок k’₁l’₁ — кратчайшее расстояние между ребрами АS и ВС. Для построения проекций кратчайшего расстояния в системе V/H находим по линии связи точку l₁ и проводим l₁k₁ параллельно оси проекций Х₂ , после чего при помощи линий связи находим основные проекции kl и k’l’.

Сущность способов вращения заключается в том, что заданная геометрическая форма путем вращения вокруг некоторой оси перемещается в пространстве до тех пор, пока она не займет частное положение по отношению к неизменной системе плоскостей проекций.

В зависимости от положения оси вращения по отношению к плоскостям проекций различают следующие способы вращения:

а) вращение вокруг осей, перпендикулярных к плоскостям проекций;

б) то же без указания положения осей вращения;

в) вращение вокруг горизонтали или фронтали;

г) вращение вокруг одного из следов плоскости (совмещение).

Рисунок 17 Рисунок 18

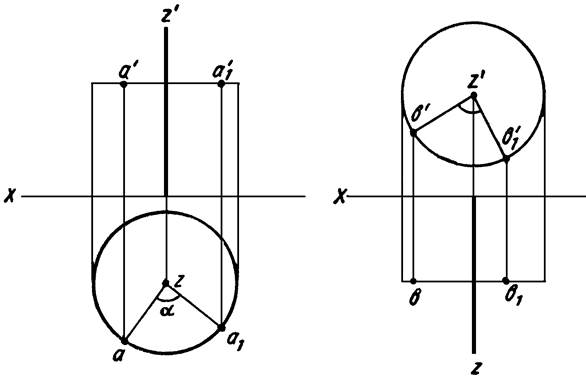
На эпюре (рисунок 17) изображена точка А и ось вращения Z, перпендикулярная к плоскости проекций H. При вращении вокруг оси Z точка А будет перемещаться по окружности, лежащей в плоскости, перпендикулярной оси вращения (параллельной плоскости проекций H). Если точку А переместить из положения А в положение A₁ т. е. повернуть ее вокруг оси Z, на некоторый угол α , то ее горизонтальная проекция (а) займет положение a₁, описав при этом дугу радиуса za (za — радиус вращения), а фронтальная проекция (а’) точки переместится по прямой a’a’₁, параллельной оси X.

Если ось вращения Z (рисунок 18) перпендикулярна к плоскости проекций V, то при вращении точки В вокруг этой оси фронтальная проекция траектории её перемещения будет окружностью, а горизонтальная — прямой, параллельной оси X.

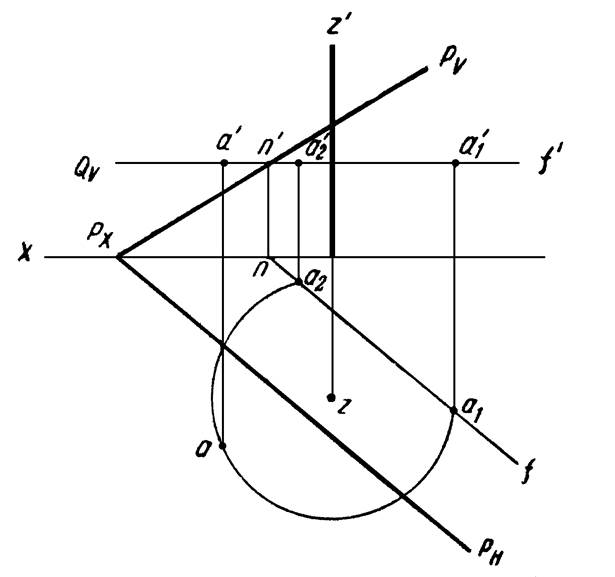
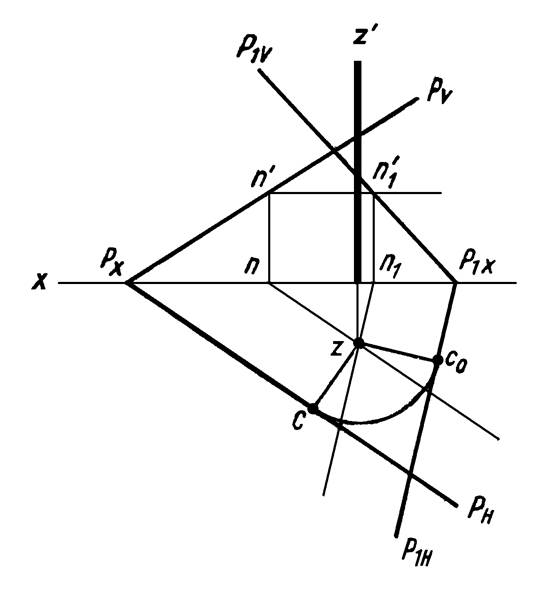
Пример 9. Совместить точку А с плоскостью Р путем вращения ее вокруг заданной оси Z (рисунок 19).

При вращении вокруг оси Z, точка А опишет окружность в плоскости Q, перпендикулярной этой оси. Плоскость Q пересечет заданную плоскость Р по горизонтали NF. Очевидно, точка А окажется в плоскости Р тогда, когда окружность, описываемая точкой А, пересечет горизонталь NF. Задача, как видно из чертежа, имеет два решения.

Чтобы повернуть прямую АВ (рисунок 20) на некоторый угол α, достаточно повернуть на заданный угол две принадлежащие, ей точки. Из чертежа видно, что треугольники abz и a₁b₁z₁ равны между собой (по двум сторонам и углу между ними), а из их равенства следует, что ab = a₁b₁, т. е. величина горизонтальной проекции отрезка при вращении его вокруг оси, перпендикулярной Н, не изменяется, изменяется только ее положение относительно оси проекций. Это обстоятельство позволяет упростить построения при решении приведенного примера

Рисунок 20 Рисунок 21

На рисунке 21 для поворота прямой АВ вокруг оси Z на угол α из z, опущен перпендикуляр на ab. Затем точка с повернута на заданный угол α, через точку c₁ проведена прямая, перпендикулярная радиусу c₁z, и отложены отрезки c₁a₁=са и c₁b₁=cb.

Вращение плоскости вокруг оси, перпендикулярной плоскости проекций, осуществляется путем вращения на один и тот же угол в одном и том же направлении точек и прямых, которыми задана плоскость.

На рисунке 22 плоскость, заданная треугольником АВС, повернута вокруг оси Z. в положение, перпендикулярное фронтальной плоскости проекций (горизонтальная проекция горизонтали А1 заняла положение, перпендикулярное оси X).

Если же плоскость задана следами, то для поворота плоскости на некоторый угол необходимо повернуть на заданный угол один из ее следов и горизонталь или фронталь этой плоскости (рисунок 23).

Таким образом, при вращении любой пространственной формы около оси, перпендикулярной одной из плоскостей проекций, проекция ее на эту плоскость по своей величине не изменится. Изменится лишь положение этой проекции относительно оси проекций. Пользуясь этим, для решения той или иной задачи можно применять способ вращения, не изображая на чертеже осей вращения.

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 267
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 603
• БГУ 155
• БГУИР 391
• БелГУТ 4908
• БГЭУ 963
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 120
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1966
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 299
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 408
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 498
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 131
• ИжГТУ 145
• КемГППК 171
• КемГУ 508
• КГМТУ 270
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2910
• КрасГАУ 345
• КрасГМУ 629
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 138
• КубГУ 109
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 369
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 331
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 637
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 455
• НИУ МЭИ 640
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 213
• НУК им. Макарова 543
• НВ 1001
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1993
• НГУЭУ 499
• НИИ 201
• ОмГТУ 302
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 120
• РАНХиГС 190
• РОАТ МИИТ 608
• РТА 245
• РГГМУ 117
• РГПУ им. Герцена 123
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 123
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 131
• СПбГАСУ 315
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 146
• СПбГПУ 1599
• СПбГТИ (ТУ) 293
• СПбГТУРП 236
• СПбГУ 578
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 194
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 379
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1654
• СибГТУ 946
• СГУПС 1473
• СибГУТИ 2083
• СибУПК 377
• СФУ 2424
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 325
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 309

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Источник

Задание 3. Многогранники

4.1. Краткие теоретические сведения

Многогранниками называются тела, ограниченные плоскими n-угольниками, которые называются гранями . Линии пересечения граней называются ребрами , точки пересечения ребер – вершинами. Для всех многогранников справедлива формула Эйлера: сумма граней и вершин за минусом числа ребер есть величина постоянная: Г + В – Р = 2.

Наиболее распространенными в технике многогранниками являются правильные и неправильные, прямые и наклонные призмы и пирамиды. Призмой называется многогранник, в основании которого находится плоский n-угольник, а остальные грани являются в общем случае параллелограммами. Пирамидой называется многогранник, в основании которого находится плоский n-угольник, а боковыми гранями являются треугольники с общей вершиной. На эпюре многогранники задаются проекциями ребер, так называемой сеткой ребер .

Типовой задачей для многогранников является задача о пересечении многогранников плоскостями частного и общего положения. Для построения фигуры сечения многогранника плоскостью используют следующие приемы:

• • определение каждой вершины сечения, как точки пересечения ребер многогранника с секущей плоскостью ( способ ребер );

• построение стороны сечения, как линии пересечения с секущей плоскостью граней многогранника ( способ граней ).

Чаще применяется первый из заданных приемов, второй же целесообразно применять в тех случаях, когда грани многогранника являются проецирующими плоскостями, линии пересечения которых с секущей плоскостью общего положения строятся очень просто.

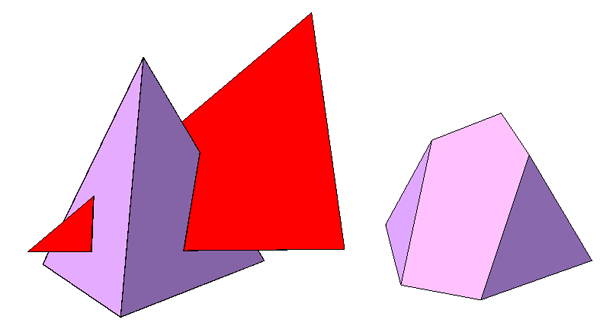
а б
Рисунок 4.1 – Пересечение пирамиды плоскостью (а — задание, б — результат)

В методе ребер несколько раз (по числу пересекаемых ребер) решается задача о пересечении прямой (ребра) с плоскостью (секущей плоскостью). В этом случае находятся точки 1, 2, 3 (рис. 4.1). Найденные точки являются вершинами сечения пирамиды плоскостью.

В методе граней несколько раз решается типовая задача о пересечении двух плоскостей (граней многогранника и секущей плоскости), в которой находят линии 1-2, 2-3, 3-1, являющиеся сторонами многоугольника (в данном примере, треугольника сечения). Если секущая плоскость является плоскостью частного положения, то задача решается упрощенно.

4.2. Способ перемены плоскостей проекций

Сущность способа перемены плоскостей проекций заключается в том, что положение геометрических элементов (точек, прямых, фигур, тел) в пространстве остается неизменным, а система плоскостей проекций заменяется новой, по отношению к которой эти элементы занимают положение, наиболее удобное для решения той или иной задачи.

В ряде случаев для решения задачи бывает достаточно заменить новой плоскостью одну из основных плоскостей проекций – фронтальную или горизонтальную. В других же случаях замена лишь одной плоскости проекций вопроса не разрешает и бывает необходимо последовательно заменить новыми плоскостями обе основные плоскости проекций.

При замене основной плоскости проекций новой плоскостью эта последняя должна располагаться по отношению к остающейся основной плоскости проекций перпендикулярно.

Рассмотрим способ перемены плоскостей проекций на примерах.

Для того чтобы данная прямая общего положения m=АВ оказалась линией уровня, следует ввести новую плоскость проекций π₄, которая была бы ей параллельна (рис. 4.2 и 4.3).

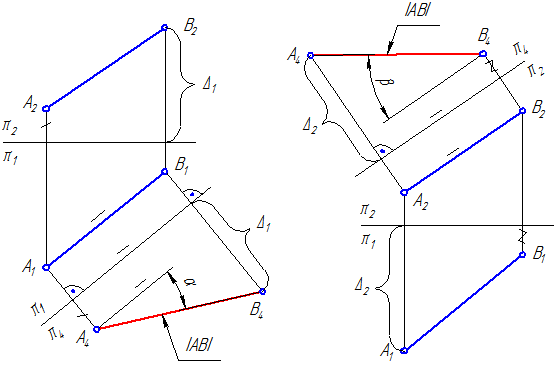
Рисунок 4.2 Рисунок 4.3

На Рисунке 4.2 введена плоскость π₄, параллельная прямой m и перпендикулярная к плоскости π₁; по новым линиям связи от оси π₁/π₄ откладываем расстояния от точек А и В до плоскости π₁ (отмеченное штрихом и D₁). В новой системе плоскостей проекций π₁/π₄ прямая m является линией уровня.

На Рисунке 4.3 плоскость π₄ параллельна прямой m=АВ и перпендикулярна к плоскости π₂. Прямая m в системе π₂/π₄ является линией уровня.

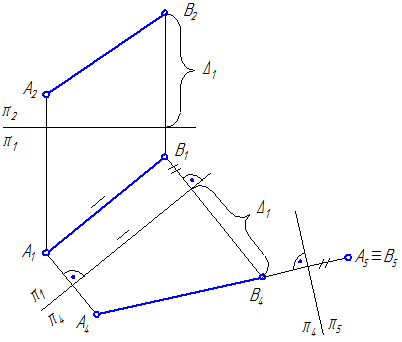
Для того чтобы прямая линия была проецирующей прямой вводится плоскость проекций, перпендикулярная к ней. Для прямой общего положения требуется провести две замены плоскостей проекций. На Рисунке 4.4 прямая m=АВ спроецирована на параллельную ей плоскость π₄. Затем вводится плоскость проекций π₅, перпендикулярная m₄. В системе плоскостей проекций π₅/π₄ прямая m проецируется в точку.

Рисунок 4.4 – Проецирование отрезка прямой в точку

Чтобы определить натуральную величину плоской фигуры общего положения (Рисунок 4.5), требуется сначала ввести такую плоскость проекций π₄, чтобы образовалась система, в которой плоскость α, заданная треугольником АВС будет проецирующей. Данную подзадачу можно решить, введя дополнительную плоскость проекций π₄ перпендикулярно либо горизонтальной проекции горизонтали, либо фронтальной проекции фронтали. Затем вводится дополнительная плоскость π₅, перпендикулярная к плоскости π₄ и параллельная плоскости α .

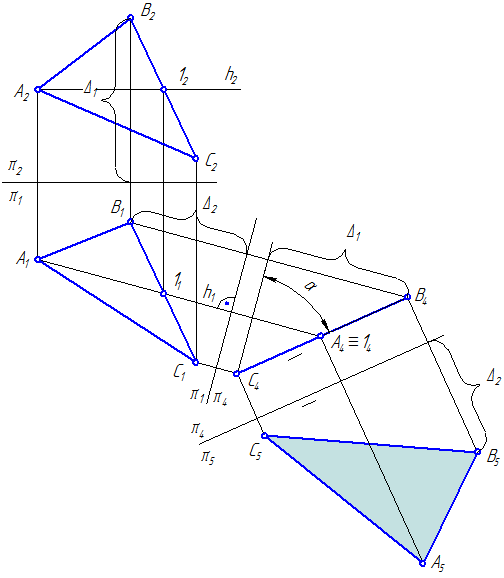
Рисунок 4.5 – Определение натуральной величины треугольника

4.3. Развертывание поверхностей

Разверткой называется плоская фигура, получаемая путем совмещения с плоскостью чертежа поверхности тела.

Построение разверток имеет большое значение в таких областях техники, как котлостроение, судостроение, кровельное и жестяночное дело, продукция которых изготовляется из листового материала.

Точные развертки могут быть построены лишь для линейчатых поверхностей, смежные положения образующих которых параллельны (цилиндрическая поверхность) или пересекаются (коническая поверхность).

Для нелинейчатых поверхностей, образующей которых является кривая линия (например, сферическая поверхность), можно построить развертки лишь приближенные. С этой целью такие поверхности разбиваются на небольшие элементы, и каждая такая часть кривой поверхности заменяется плоскостью. Это означает, что данная кривая поверхность заменяется вписанным в нее многогранником, развертка которого приближенно принимается за развертку кривой поверхности.

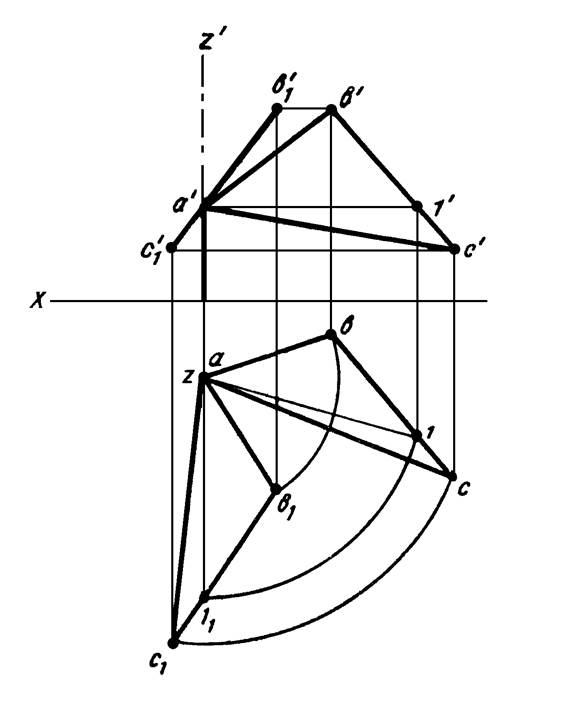
Развертка боковой поверхности пирамиды (Рисунок 4.7) состоит из трех треугольников, представляющих в истинном виде боковые грани пирамиды.

Для построения развертки необходимо предварительно определить истинные длины боковых ребер пирамиды. Повернув эти ребра вокруг высоты пирамиды до положения параллельного плоскости ?₂, на фронтальной плоскости проекций получим их истинные длины в виде отрезков S₂ A ₂, S₂ B ₂, S₂ C ₂ (Рисунок 4.6).

Построив по трем сторонам S₂ A ₂, S₂ B ₂ и A₁B₁ грань пирамиды ASB (Рисунок 4.7), пристраиваем к ней смежную грань – треугольник BSC, а к последнему – грань CSA. Полученная фигура представит собою развертку боковой поверхности данной пирамиды.

Для получения полной развертки к одной из сторон основания пристраиваем основание пирамиды – треугольник АВС.

Для построения на развертке линии, по которой поверхность пирамиды пересечется плоскостью α (Рисунок 4.7), следует нанести на ребра SA, SB и SC, соответственно, точки 1, 2 и 3, в которых эта плоскость пересекает ребра, определив истинные длины отрезков S1, S2 и S3.

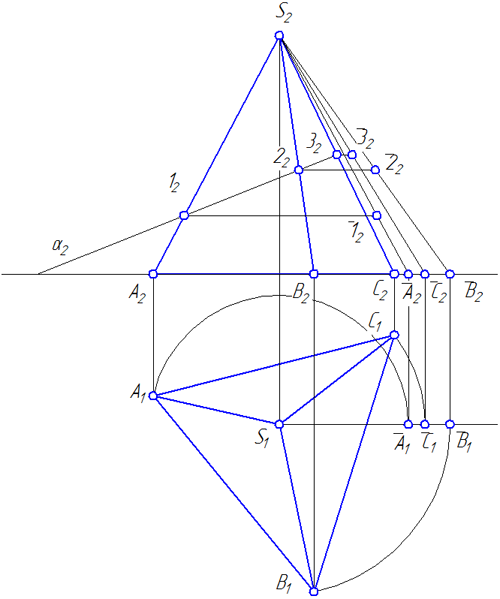
Рисунок 4.6 – Определение истинных длин ребер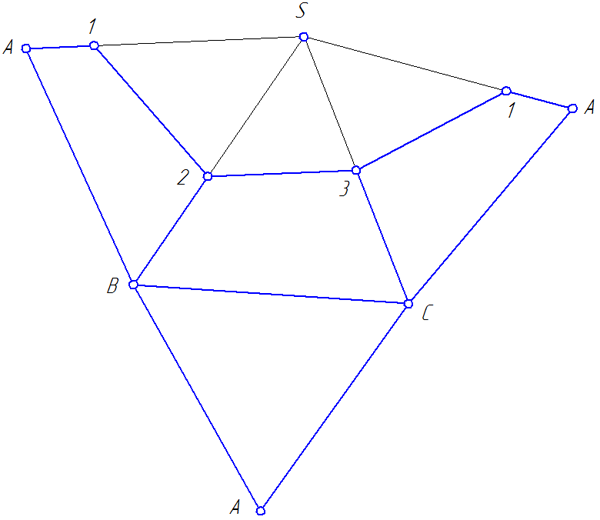

Рисунок 4.7 – Построение развертки

4.4. Задание 3. Построение натурального вида сечения пирамиды плоскостью

4.4.1. Условие задания

Задание следует выполнять в соответствии с алгоритмом:

1. 1. По координатам вершин (Таблицы 3.1- 3.3) построить: две проекции пирамиды 1234S;

1. 1. Выполнить две проекции сечения пирамиды плоскостью общего положения АВС (Таблица 3.4);

1. 1. Найти натуральный вид сечения способом перемены плоскостей проекций;

1. Выполнить развертку верхней отсеченной части пирамиды.

4.4.2. Рекомендации по выполнению задания № 2

Порядок выполнения задачи следующий:

1. Построить горизонтальные и фронтальные проекции пирамиды и 1234S и плоскости ∆АBC (Рисунок 4.8);
2. Способом ребер или способом граней построить проекции сечения пирамиды 1234S плоскостью ∆АBC.

Способ ребер заключается в том, что ребро пирамиды (например, 1S) заключается во фронтально-проецирующую плоскость γ: γπ₂≡1₂S₂. Затем выполняется построение точки 8 пересечения ребра 1S с плоскостью γ:

Аналогично выполняется построение остальных точек искомого сечения.

Способом граней строятся линии пересечения с помощью плоскостей-посредников;

Рисунок 4.8 – Построение сечения

1. Способом перемены плоскостей проекций найти натуральный вид сечения 56789.

Сущность способа перемены плоскостей проекций состоит в том, что положение геометрического образа (прямой, плоскости, поверхности) в пространстве остается неизменным, а система плоскостей проекций π₁/π₂ дополняется плоскостями, образующими с π₁ или π₂, либо между собой системы двух взаимно перпендикулярных плоскостей проекций. Расположение новой плоскости проекций по отношению к геометрическим образам выбирается в зависимости от условия задачи.

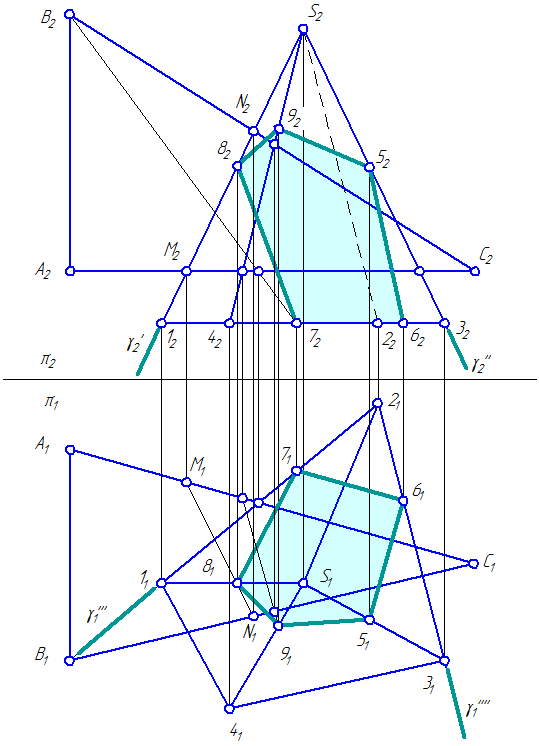
В данной задаче необходимо дважды ввести новые плоскости проекций: в системе плоскостей π₁/π₄ сечение 56789 станет проецирующей плоскостью, а в системе плоскостей проекций π₄/π₅ – плоскостью уровня;

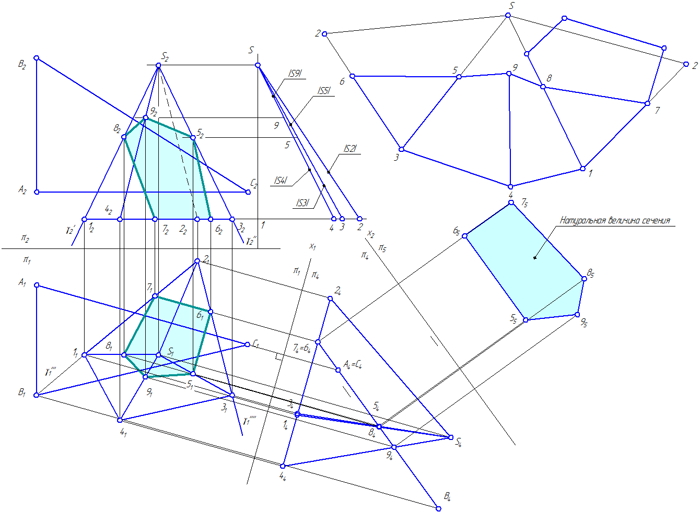
Рисунок 4.9 – Пересечение пирамиды плоскостью общего положения

1. Выполнить развертку нижней отсеченной части пирамиды.

Видеопример выполнения задания №3

4.5. Варианты задания 3

Таблица 3.1– Значения координат точек (для вариантов с 1 по 10)

S	1	2	3	4
X	50	90	30	10	70
Y	50	50	5	70	80
Z	90	10	10	10	10

Таблица 3.2– Значения координат точек (для вариантов с 11 по 20)

S	1	2	3	4
X	50	90	30	10	70
Y	50	50	5	70	80
Z	90	0	0	0	0

Таблица 3.3– Значения координат точек (для вариантов с 21 по 30)

S	1	2	3	4
X	50	100	25	5	80
Y	50	50	5	70	80
Z	100	10	10	10	10

Таблица 3.4– Значения координат точек

Вариант	Координаты (x, y, z) точек			Вариант	Координаты (x, y, z) точек
	А	В	С		А	В	С
1	100;15;30	35; 85; 90	10; 45; 30	16	90; 0; 0	100; 50; 70	5; 55; 40
2	65; 10; 0	100; 50; 80	20; 80; 80	17	95; 35; 40	50; 35; 0	5; 65; 50
3	100; 25;40	15; 90; 90	50; 15; 0	18	50; 50; 45	0; 55; 0	100; 20; 5
4	30; 80; 90	20; 25; 0	100; 25; 40	19	30; 90; 60	90; 30; 20	0; 35; 0
5	100; 15; 20	100; 60; 90	10; 45; 20	20	95; 15; 0	5; 60; 20	70; 85; 80
6	90; 0; 0	100; 50; 80	5; 55; 40	21	100;15;30	35; 85; 90	10; 45; 30
7	95; 35; 50	50; 35; 0	5; 65; 50	22	65; 10; 0	100; 50; 80	20; 80; 80
8	50; 50; 55	0; 55; 5	100; 20; 5	23	100; 25;40	15; 90; 90	50; 15; 0
9	30; 90; 70	90; 30; 30	0; 35; 0	24	30; 80; 90	20; 25; 0	100; 25; 40
10	95; 15; 10	5; 60; 30	70; 85; 80	25	100; 15; 20	100; 60; 90	10; 45; 20
11	100;15;20	35; 85; 80	10; 45; 30	26	90; 0; 0	100; 50; 80	5; 55; 40
12	65; 10; 0	100; 50; 70	20; 80; 80	27	95; 35; 50	50; 35; 0	5; 65; 50
13	100; 25;30	15; 90; 80	50; 15; 0	28	50; 50; 55	0; 55; 5	100; 20; 5
14	30; 80; 80	20; 25; 0	100; 25; 40	29	30; 90; 70	90; 30; 30	0; 35; 0
15	100; 15; 10	100; 60; 80	10; 45; 20	30	95; 15; 10	5; 60; 30	70; 85; 80

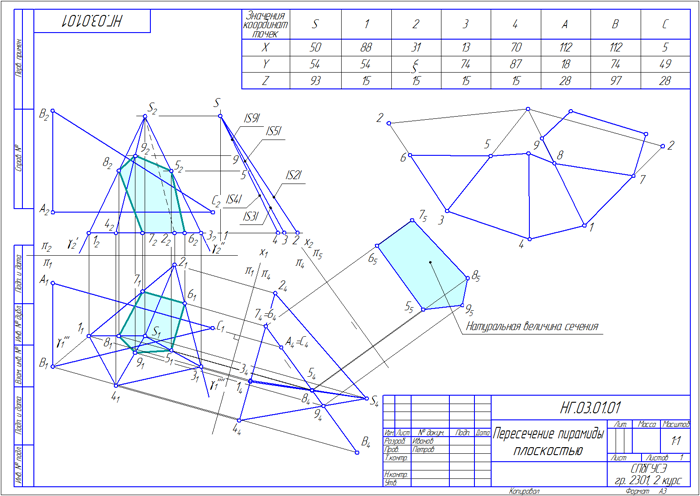
Рисунок 4.10 – Пример оформления задания 3

Источник