Методы детерминированного анализа
В настоящее время в литературе выделяют достаточно большое количество методов детерминированного факторного анализа или их еще называют методами анализа количественного влияния факторов на изменение результативного показателя. К наиболее используемым на предприятии методам относят: цепные подстановки, метод абсолютных разниц, метод относительных разниц, метод пропорционального деления и долевого участия, интегральный метод.
Первые три метода основаны на приеме элиминирования. Элиминировать (от лат. eliminare — исключать, устранять) — значит исключать влияния некоторых факторов с целью выделения какого-нибудь одного.
Метод цепных подстановок, широко применяющийся на практике, позволяет раскрыть взаимосвязь отдельных факторов и измерить их влияние на отклонение от плана тех показателей, которые непосредственно от них зависят. Подстановкой называется замена базовой величины частного (факторного) показателя отчетной. Число подстановок равно числу входящих в расчетную формулу частных показателей, поскольку при определении общей величины изменения обобщающего (результативного) показателя приводится расчет базовой величины, где все показатели базовые.
Сущность метода цепных подстановок заключается в последовательной и постепенной замене планового значения отдельных показателей, входящих в расчетную формулу, отчетным значением этих показателей и измерении влияния произведенной замены на изменение величины изучаемого обобщающего показателя.
Первоначально в расчетную формулу подставляют все плановые значение и определяют так называемый базовый (плановый) показатель. Затем в ту же формулу подставляют поочередно отдельные отчетные показатели, а все остальные величины остаются плановыми. После каждой замены того или иного показателя результат расчета сравнивают с базовым (плановым), который принимают на 100%. Полученное отклонение рассматривают как отражение влияния данного отчетного показателя, поскольку все остальные показатели, как в базовом, так и во вновь выполненном расчете одинаковы. Степень влияния тех или иных факторов на конечный результат определяют не только в абсолютных величинах, но и в процентах.
Рассмотрим расчет влияния факторов a, b на прирост результативного показателя f в мультипликативных моделях типа f = ab. Здесь следует обратить внимание что на первом месте всегда должен идти количественный фактор (например — объем), а потом качественный (цена). Для изучения влияния двух факторов на результативный показатель расчеты выполняются в следующем порядке:
— определяют базовое значение результативного показателя f0 = a0b0;
— определяют влияние первого показателя-фактора на анализируемый показатель. При этом базовое значение фактора a0 заменяют текущим значением a1, т.е. fa – a1b0;
— определяют степень влияния первого показателя-фактора на анализируемый показатель при плановой базе. Для этого из расчетной величины fa вычитают базовую величину f0:
Если в результате расчета получается ответ со знаком плюс, то это значит, что данный показатель-фактор способствовал улучшению анализируемого показателя, его увеличению; ответ со знаком минус свидетельствует о снижении уровня анализируемого показателя;
— определяют влияние показателя-фактора на анализируемый показатель в процентах:
; (3.6)
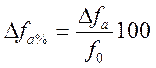
— аналогично определяют влияние другого показателя- фактора, входящего в формулу, по которой рассчитывают анализируемый показатель:
(3.8)
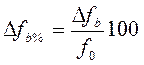
— определяют правильность предыдущих построений. При этом сумма найденных величин факторных отклонений должна соответствовать общему изменению рассматриваемого показателя:
Следует отметить, что на практике, как правило, такого равенства между суммой факторных отклонений и общим изменением результативного показателя не получается. При использовании метода цепных подстановок влияние каждого показателя рассматривается изолировано, без учета его взаимосвязи с другими показателями. В действительности между показателями существует определенная зависимость – изменение одного из показателей вызывает изменение других.
В результате взаимосвязанного влияния показателей образуется, так называемый, «неразложенный остаток». Существует несколько вариантов использования неразложенного остатка:
· неразложенный остаток условно прибавляют к влиянию качественного показателя (наиболее распространенный вариант);
· неразложенный остаток делят на равные части по факторам;
· неразложенный остаток делят пропорционально темпам прироста соответствующих факторов;
· пренебрегают неразложенным остатком.
С целью избавления от неразложенного остатка пользуются более сложными методами, например, интегральным, логарифмическим, кольцевым и др.
Метод абсолютных разниц. Как и метод цепных подстановок, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных моделях и смешанных моделях типа f – a (b – c). Хотя его использование ограничено, но благодаря своей простоте этот метод широко применяется в анализе финансово-хозяйственной деятельности предприятия.
При использовании этого метода величина влияния факторов рассчитывается умножением абсолютного прироста анализируемого фактора на базовую величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Рассмотрим применение метода на примере мультипликативной факторной модели типа f – abcd. Имеются базовые (плановые) и фактические значения по каждому факторному показателю, а также их абсолютные отклонения:
Определим изменение величины результативного показателя за счет влияния каждого фактора:
Как видно из приведенной схемы расчет строится на последовательной замене базовых значений факторных показателей их отклонениями, а затем фактическим уровнем этих показателей.
Здесь также как и в методе цепных подстановок необходимо следить за соотношением алгебраической суммы прироста результативного показателя за счет отдельных факторов (Δfa + Δfb + Δfc + Δfd) и общим его приростом (f1 – f0). Если равенство между ними не достигнуто, то образуется неразложенный остаток, избавиться от которого можно любым из вариантов, описанных выше.
Метод относительных разниц, как и предыдущий, применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях и смешанных моделях типа f = a (b – c). Он значительно проще метода цепных подстановок, что при определенных обстоятельствах делает его достаточно эффективным для использования в анализе финансово-хозяйственной деятельности предприятия. Это касается тех случаев, когда исходные данные содержат уже определенные ранее относительные отклонения факторных показателей в процентах (или коэффициентах).
Рассмотрим применение метода на примере мультипликативной модели типа f = abc.
Сначала необходимо рассчитать относительные отклонения факторных показателей в процентах:
; (3.18)
; (3.19)
. (3.20)
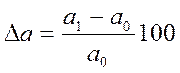
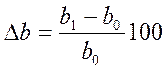
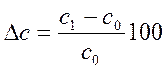
Тогда изменение величины результативного показателя за счет влияния каждого фактора определяется следующим образом:
; (3.21)
; (3.22)
(3.23)
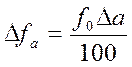
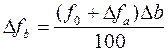
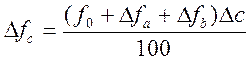
Для расчета влияния первого фактора на изменение результативного показателя необходимо базовую величину результативного показателя умножить на относительный прирост первого фактора, выраженного в процентах, и результат разделить на 100. Чтобы рассчитать влияние второго фактора, нужно к базовой величине результативного показателя прибавить изменение его за счет первого фактора, далее полученную сумму умножить на относительный прирост второго фактора, выраженного в процентах, и результат разделить на 100. Влияние третьего фактора определяется аналогично: к базовой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора (в процентах) и т.д.
Также как и в методе абсолютных разниц здесь следует учитывать возможность получения нераспределенного остатка.
Метод относительных разниц удобно применять в тех случаях, когда требуется рассчитать влияние большого числа факторов (более 8). При этом, в отличие от предыдущих методов, значительно сокращается объем вычислений.
Метод пропорционального деления и долевого участия в ряде случаев могут быть использованы для определения величины влияния факторов на изменение результативного показателя. Это касается тех случаев, когда имеют дело с аддитивными моделями и смешанными моделями типа:
. (3.24)
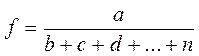
Рассмотрим применение метода пропорционального деления на примере аддитивной модели f = a + b + c.
Изменение величины результативного показателя за счет влияния каждого фактора определяется следующим образом:
; (3.25)
; (3.26)
. (3.27)
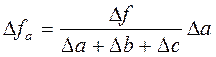
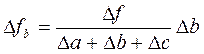
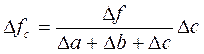
При использовании моделей смешанного типа расчеты, производимые по методу пропорционального деления, значительно усложняются. Так, для определения изменения величины результативного показателя за счет влияния каждого фактора, во- первых, строится дерево факторов, во-вторых, вводится и рассчитывается коэффициент, который учитывает иерархический уровень факторов, входящих в модель.
Применяя метод долевого участия (если имеется та же аддитивная модель, что и в предыдущем примере) сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя:
; (3.28)
; (3.29)
. (3.30)
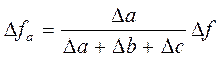
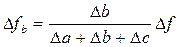
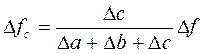
Интегральный метод отличается высокой точностью расчетов, по сравнению со всеми разобранными ранее методами и применяется для измерения влияния факторов на прирост результативного показателя в мультипликативных, кратных и смешанных моделях. Его сущность заключается в суммировании приращений функции, определенной как частная производная, умноженная на приращение аргумента на бесконечно малых промежутках, при соблюдении необходимых условий. Для этого в интегральном методе пользуются специально определенными формулами. Основные из них для разных моделей приведены в таблице 3.2.
Таким образом, использование интегрального метода не требует знания всего процесса интегрирования. Достаточно в готовые рабочие формулы из таблицы 3.2 подставить необходимые числовые данные и сделать соответствующие расчеты.
Источник
Приемы детерминированного факторного анализа
Для определения влияния факторов в детерминированных факторных моделях используются следующие основные методы: цепных подстановок, абсолютных и относительных разниц, долевого участия, индексный метод, интегральный метод.
Большая часть традиционных (специальных) приемов детерминированного факторного анализа основана на элиминировании.
Смысл элиминирования заключается в следующем: Все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, затем изменяются два, три и т.д. при неизменности остальных.
Используют логику элиминирования методы: цепных подстановок, индексный, абсолютных и относительных (процентных) разниц.
Прием цепных подстановок используется во всех видах детерминированных факторных моделей для измерения изолированного влияния факторов на изменение результативного показателя. Факторы в модели должны быть последовательно расположены: от количественных к качественным, от более общих к более частным. Данное требование связано с признанием более активной роли в изменении результативного показателя качественного фактора, вследствие чего возникающий от совместного влияния факторов неразложимый остаток приписывается именно ему.
Порядок применения. Рассчитывается ряд скорректированных значений результативного показателя путем последовательной замены базисных значений факторов на фактические значения.
Разность между последовательно полученными результативными показателями представляет величину их изменения вследствие влияния соотвествующего фактора (таблица 4.1).
Исходная модель: П = А * В * С * D, в которой исследуются факторы базисного (А0,…D0) и отчетного периода (А1,…D1). В исходную базисную модель последовательно подставляются факторы отчетного периода.
Для проверки правильности расчетов методами факторного анализа составляется баланс отклонений, сумма которых должна быть равна абсолютному отклонению результивного показателя.
| № подстановки | Порядок подстановки факторов | Результативный показатель, П | Изменение результативного показателя, DП |
| А0 * В0 * С0 * D0 | П0 | — | |
| А1* В0 * С0 * D0 | ПА | DП А =ПA-П0 | |
| А1 * В1 * С0 * D0 | ПB | DП B = ПB-ПA | |
| А1 * В1 * С1 * D0 | ПC | DП C = ПC-ПB | |
| А1 * В1 *С1 *D1 | ПD=П1 | DП D = П1-ПC | |
| Баланс отклонений: D П = D П A + D П B + D П C + D П D |
Прием абсолютных разниц используется аналогично приему цепных подстановок в детерминированных факторных моделях, в том числе мультипликативных и смешанных типа: Y = (A-B)*C и Y = A*(B-C). Необходимо следовать тем же требованиям подстановок показателей.
Порядок применения.Величина влияния отдельного фактора на изменение результативного показателя определяется путем умножения абсолютного прироста исследуемого фактора на базисную величину факторов, которые в модели находятся справа от него, и на фактическую величину факторов, расположенных слева.
В случае исходной мультипликативной модели П=А*В*С*D получим: изменение результативного показателя:
5.Общее изменение (отклонение) результативного показателя (баланс отклонений):DП=D П A +D П B +D П C +D П D
Баланс отклонений должен соблюдаться (так же как в приеме цепных подстановок).
Прием относительных (процентных) разниц также применяется для измерения изолированного влияния факторов на изменение результативного показателя в детерминированных факторных моделях, в том числе мультипликативных и смешанных (комбинированных) типа: Y = (A-B)*C. Его целесообразно применять, когда известны определенные ранее относительные отклонения факторных показателей в процентах или коэффициентах. Требования к последовательности расположения факторов в модели отсутствуют. Результативный признак изменяется пропорционально изменению факторного признака.
Порядок применения. Величина влияния отдельного фактора на изменение результативного показателя определяется путем умножения базисного (планового) значения результативного показателя на относительный прирост факторного признака.
Y=А*В*С
Изменение результативного показателя:
1. За счет фактора А:
, где 
2. За счет фактора В:
где 
3. За счет фактора С:
, где 
Баланс отклонений: общее отклонение результативного показателя складывается из отклонений по факторам: DY= Y1 — Y0 = D Y A +D Y B +D Y C
Интегральный метод выступает альтернативой вышерассмотренным приемам детерминированного факторного анализа в измерении влияния факторов на изменение результативного показателя. По сравнению с приемами, основанными на элиминировании, дает более точные результаты, поскольку дополнительный прирост результативного показателя за счет взаимодействия факторов распределяется пропорционально их изолированному воздействию на результативный показатель. Отличается также и сложностью вычислений, возрастающей пропорционально увеличению числа факторов в моделях. Может использоваться в таких детерминированных факторных моделях, как мультипликативные, кратные и смешанные типа 
.
Порядок применения. Величина влияния отдельного фактора на изменение результативного показателя определяется на основе формул для разных факторных моделей, выведенных с применением дифференцирования и интегрирования в факторном анализе.
Обобщающий (результативный) показатель рассматривается как функция многих переменных (факторов).
Ниже приведены типы факторных моделей и рабочие формулы для определения влияния факторов.
1. f = x * y
Изменение результативного показателя за счет фактора х:
; за счет ΔY B фактора у: 
;
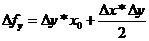
Общее изменение результативного показателя: D¦ = D¦x + D¦у
2. f = x * y * z
Изменение результативного показателя за счет фактора х:
;
за счет фактора y:
;
за счет фактора z:
;
Баланс отклонений: D¦ =D¦х +D¦у + D¦ z
3. f= 
Изменение результативного показателя за счет фактора х:
;
за счет фактора y:
;
Баланс отклонений: D¦ =D¦х + D¦у
4. f= 
Изменение результативного показателя за счет фактора х:
;
за счет фактора y:
;
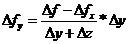
за счет фактора z:
Баланс отклонений: D¦ =D¦x +D¦у + D¦ z
Индексный прием экономического анализа используется в статистике, планировании и анализе хозяйственной деятельности для количественной оценки роли отдельных факторов в динамике изменений обобщающих показателей. Так, изучая зависимость объема выпуска продукции на предприятии от изменений численности работающих и производительности их труда, можно воспользоваться следующей системой взаимосвязанных индексов:
; 
; 
, где I N – общий индекс изменения объема выпуска продукции; I R — индивидуальный индекс (факторный) изменения численности работающих; I λ — факторный индекс изменения производительности труда работающих; R0, R1 — среднегодовая численность персонала соответственно в базисном и отчетном периодах; λ0, λ1 – среднегодовой выпуск продукции на одного работающего в базисном и отчетном периодах.
Принцип построения факторной модели индексов учитывает следующее правило: если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода.
Индексный метод позволяет провести разложение по факторам не только относительных, но и абсолютных отклонений обобщающего показателя. Так, величина абсолютного отклонения объема выпуска товарной продукции будет рассчитана следующим образом:
, где — 
абсолютное изменение объема выпуска товарной продукции.
Изменение объема продукции за счет изменения численности работающих определяется по формуле: 
.
Изменение объема продукции за счет изменения производительности труда работающих определяется по формуле: 
.
Метод индексов не дает общего разложения абсолютных отклонений обобщающего показателя при числе факторов более двух и если их связь не является мультипликативной.
Прием пропорционального деления и долевого участия используется для измерения изолированного влияния отдельных факторов на изменение результативного показателя в детерминированных факторных моделях, в том числе: аддитивных и комбинированных типа: 
. Целесообразно использовать данный прием в случаях, когда значения факторов в различных периодах неизвестны, но известна величина их изменения.
Порядок применения. Величина влияния отдельного фактора на результативный показатель пропорциональна доле изменения данного фактора в общем суммарном изменении факторов.
В случае исходной аддитивной одноуровневой модели: Y = А + В + С
Изменение результативного признака:
1. За счет фактора А: 
;
2. За счет фактора В: 
;
3. За счет фактора С: 
Баланс отклонений: Общее отклонение результативного показателя складывается из отклонений по факторам: DY = Y1 — Y0 = D Y A + D Y B + D Y C
При наличии в мультипликативной модели комплексных факторов она может быть преобразована в многоуровневую с дальнейшим определением влияния факторов второго уровня на результативный признак (рис. 3.2).
Рис.3.2. Схема взаимодействия факторов
Детерминированная факторная модель будет выглядеть следующим образом: 
, где B= C+D. Или та же формула: 
. Для определения величины долевого участия влияния факторов С и D на результативный показатель Yсначала необходимо найти влияние факторов 1-го уровня А и В:
; 
; 
; 
.
Затем находится величина долевого участия факторов 2-го уровня:
1. Величина изменения за счет фактора C:
;
2. За счет фактора D:
3. Баланс отклонений ΔY= ΔY1— ΔY0 = ΔY A + ΔY B = ΔY A + (ΔY C + ΔY D )
Источник
