Решение задач различными методами и способами
Презентация содержит приёмы работы над задачами на уроках математики в начальной школе
Содержимое разработки
Решение задач различными методами и способами
Куличенко Валентина Геннадьевна
«Славгородский педагогический колледж»
Умение решать задачу различными способами связывается с развитием гибкости мышления и играет определенную роль в развитии умственных способностей и математического мышления.
Обучение решению задач различными способами способствует более глубокому осознанию задачной ситуации, пониманию взаимосвязей между величинами, входящими в задачу, между данными и искомыми, развивает наблюдательность и математическую зоркость.
В методической литературе отмечается, что решение задачи различными способами часто бывает более полезным, чем решение одним способом нескольких задач.
При оценке разных способов решения активно используются такие умственные операции, как анализ,
что оказывает положительное влияние на развитие умственных способностей учащихся.
Методы решения задач
- арифметический;
- алгебраический ;
- графический ;
- практический ;
- табличный ;
- логический ;
- смешанный.
основан на выборе арифметических действий, обусловленном различными связями и зависимостями между величинами, входящими в задачу, между данными и искомыми.
Задача 1. Для похода туристы закупили 96 банок консервов. В день они расходовали по 8 банок. Сколько банок консервов у них осталось после 10 дней?
Расходовали – 10 дн. по 8 б.
Задача 1. Для похода туристы закупили 96 банок консервов. В день они расходовали по 8 банок. Сколько банок консервов у них осталось после 10 дней?
Расходовали – 10 дн. по 8 б.
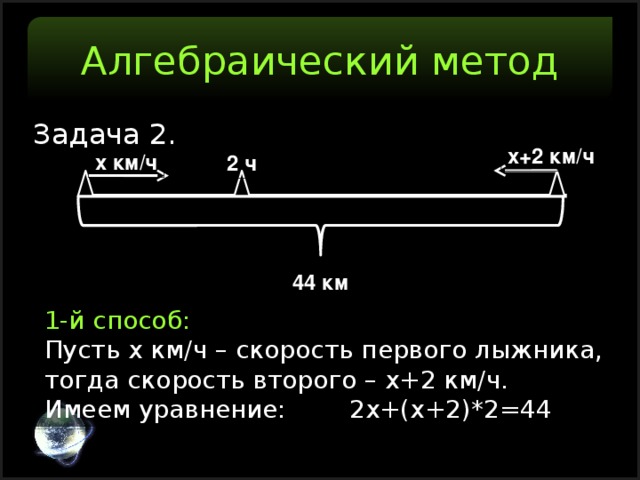
Задача 2. Из двух пунктов одновременно навстречу друг другу вышли два лыжника и через 2 ч встретились. Найдите скорость каждого лыжника, если расстояние между пунктами было 44 км, а скорость одного больше скорости другого на 2 км/ч.
Пусть х км/ч – скорость первого лыжника,
тогда скорость второго – х+2 км/ч.
Имеем уравнение: 2х+(х+2)*2=44
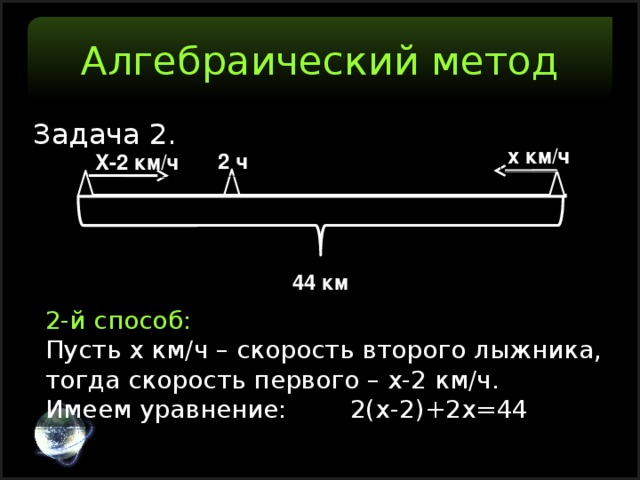
Пусть х км/ч – скорость второго лыжника,
тогда скорость первого – х-2 км/ч.
Имеем уравнение: 2(х-2)+2х=44
Задача 3. 8 яблок разложили на две тарелки. По скольку яблок на каждой тарелке?
Задача 4. Масса арбуза — 5 кг, а масса дыни на 2 кг меньше. Какова масса дыни?
Почти любую арифметическую задачу, которую решают в 1 классе, можно решить графически без выполнения арифметических действий. При этом учащиеся могут убедиться, что иногда этот подход к решению задач приводит к усложнению, а иногда позволяет легко и просто решить
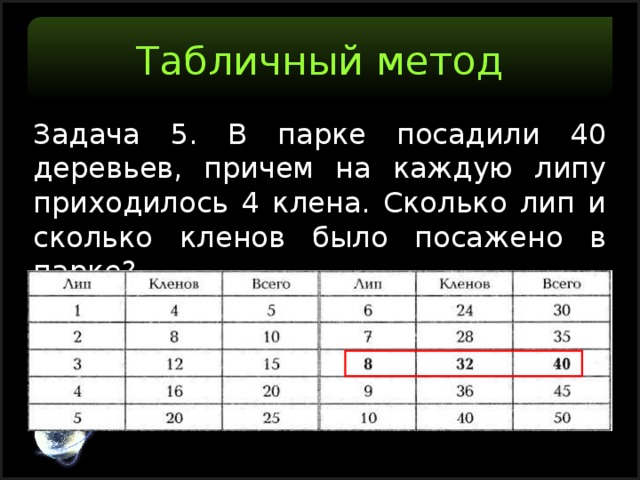
Задача 5. В парке посадили 40 деревьев, причем на каждую липу приходилось 4 клена. Сколько лип и сколько кленов было посажено в парке?
в процессе поиска решения на основе логических рассуждений можно дать ответ на вопрос задачи.
предполагает использование приемов работы по решению задач различными способами:
- беседа, в процессе которой учитель подводит учащихся к тому или иному способу решения задачи;
- обсуждение готовых решений — на доске учитель предлагает учащимся разные способы решения задачи и дает задание объяснить каждое выполняемое действие.
Задача 6. Рабочему было поручено изготовить 30 одинаковых деталей за 10 ч. Но рабочий, экономя время, успевал делать одну деталь за 15 мин. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени?
Задача 6. Рабочему было поручено изготовить 30 одинаковых деталей за 10 ч. Но рабочий, экономя время, успевал делать одну деталь за 15 мин. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени?
2) 600 — 450 = 150 (мин) —
Задача 6. Рабочему было поручено изготовить 30 одинаковых деталей за 10 ч. Но рабочий, экономя время, успевал делать одну деталь за 15 мин. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени?
- 60:15=4 (дет.) —
- 4-10=40 (дет.) —
- 40-30=10 (дет.) —
Задача 6. Рабочему было поручено изготовить 30 одинаковых деталей за 10 ч. Но рабочий, экономя время, успевал делать одну деталь за 15 мин. Сколько деталей сверх задания сделал рабочий за счет сэкономленного времени?
Источник