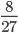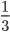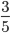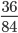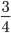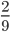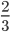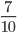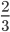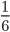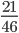При сокращении дробных выражений нужно аккуратно переносить запятые возможны два способа

Сокращение алгебраических дробей: правило, примеры.

Данная статья продолжает тему преобразования алгебраических дробей: рассмотрим такое действие как сокращение алгебраических дробей. Дадим определение самому термину, сформулируем правило сокращения и разберем практические примеры.

Смысл сокращения алгебраической дроби

В материалах об обыкновенной дроби мы рассматривали ее сокращение. Мы определили сокращение обыкновенной дроби как деление ее числителя и знаменателя на общий множитель.

Сокращение алгебраической дроби представляет собой аналогичное действие.

Сокращение алгебраической дроби – это деление ее числителя и знаменателя на общий множитель. При этом, в отличие от сокращения обыкновенной дроби (общим знаменателем может быть только число), общим множителем числителя и знаменателя алгебраической дроби может служить многочлен, в частности, одночлен или число.

К примеру, алгебраическая дробь 3 · x 2 + 6 · x · y 6 · x 3 · y + 12 · x 2 · y 2 может быть сокращена на число 3 , в итоге получим: x 2 + 2 · x · y 6 · x 3 · y + 12 · x 2 · y 2 . Эту же дробь мы можем сократить на переменную х , и это даст нам выражение 3 · x + 6 · y 6 · x 2 · y + 12 · x · y 2 . Также заданную дробь возможно сократить на одночлен 3 · x или любой из многочленов x + 2 · y , 3 · x + 6 · y , x 2 + 2 · x · y или 3 · x 2 + 6 · x · y .

Конечной целью сокращения алгебраической дроби является дробь более простого вида, в лучшем случае – несократимая дробь.

Все ли алгебраические дроби подлежат сокращению?

Опять же из материалов об обыкновенных дробях мы знаем, что существуют сократимые и несократимые дроби. Несократимые – это дроби, не имеющие общих множителей числителя и знаменателя, отличных от 1 .

С алгебраическими дробями все так же: они могут иметь общие множители числителя и знаменателя, могут и не иметь. Наличие общих множителей позволяет упростить исходную дробь посредством сокращения. Когда общих множителей нет, оптимизировать заданную дробь способом сокращения невозможно.

В общих случаях по заданному виду дроби довольно сложно понять, подлежит ли она сокращению. Конечно, в некоторых случаях наличие общего множителя числителя и знаменателя очевидно. Например, в алгебраической дроби 3 · x 2 3 · y совершенно понятно, что общим множителем является число 3 .

В дроби — x · y 5 · x · y · z 3 также мы сразу понимаем, что сократить ее возможно на х , или y , или на х · y . И все же гораздо чаще встречаются примеры алгебраических дробей, когда общий множитель числителя и знаменателя не так просто увидеть, а еще чаще – он попросту отсутствует.

Например, дробь x 3 — 1 x 2 — 1 мы можем сократить на х — 1 , при этом указанный общий множитель в записи отсутствует. А вот дробь x 3 — x 2 + x — 1 x 3 + x 2 + 4 · x + 4 подвергнуть действию сокращения невозможно, поскольку числитель и знаменатель не имеют общего множителя.

Таким образом, вопрос выяснения сократимости алгебраической дроби не так прост, и зачастую проще работать с дробью заданного вида, чем пытаться выяснить, сократима ли она. При этом имеют место такие преобразования, которые в частных случаях позволяют определить общий множитель числителя и знаменателя или сделать вывод о несократимости дроби. Разберем детально этот вопрос в следующем пункте статьи.

Правило сокращения алгебраических дробей

Правило сокращения алгебраических дробей состоит из двух последовательных действий:

• нахождение общих множителей числителя и знаменателя;
• в случае нахождения таковых осуществление непосредственно действия сокращения дроби.

Самым удобным методом отыскания общих знаменателей является разложение на множители многочленов, имеющихся в числителе и знаменателе заданной алгебраической дроби. Это позволяет сразу наглядно увидеть наличие или отсутствие общих множителей.

Само действие сокращения алгебраической дроби базируется на основном свойстве алгебраической дроби, выражаемой равенством undefined , где a , b , c – некие многочлены, причем b и c – ненулевые. Первым шагом дробь приводится к виду a · c b · c , в котором мы сразу замечаем общий множитель c . Вторым шагом – выполняем сокращение, т.е. переход к дроби вида a b .

Характерные примеры

Несмотря на некоторую очевидность, уточним про частный случай, когда числитель и знаменатель алгебраической дроби равны. Подобные дроби тождественно равны 1 на всей ОДЗ переменных этой дроби:

5 5 = 1 ; — 2 3 — 2 3 = 1 ; x x = 1 ; — 3 , 2 · x 3 — 3 , 2 · x 3 = 1 ; 1 2 · x — x 2 · y 1 2 · x — x 2 · y ;

Поскольку обыкновенные дроби являются частным случаем алгебраических дробей, напомним, как осуществляется их сокращение. Натуральные числа, записанные в числителе и знаменателе, раскладываются на простые множители, затем общие множители сокращаются (если таковые имеются).

К примеру, 24 1260 = 2 · 2 · 2 · 3 2 · 2 · 3 · 3 · 5 · 7 = 2 3 · 5 · 7 = 2 105

Произведение простых одинаковых множителей возможно записать как степени, и в процессе сокращения дроби использовать свойство деления степеней с одинаковыми основаниями. Тогда вышеуказанное решение было бы таким:

24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 — 2 3 2 — 1 · 5 · 7 = 2 105

(числитель и знаменатель разделены на общий множитель 2 2 · 3 ). Или для наглядности, опираясь на свойства умножения и деления, решению дадим такой вид:

24 1260 = 2 3 · 3 2 2 · 3 2 · 5 · 7 = 2 3 2 2 · 3 3 2 · 1 5 · 7 = 2 1 · 1 3 · 1 35 = 2 105

По аналогии осуществляется сокращение алгебраических дробей, у которых в числителе и знаменателе имеются одночлены с целыми коэффициентами.

Задана алгебраическая дробь — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z . Необходимо произвести ее сокращение.

Решение

Возможно записать числитель и знаменатель заданной дроби как произведение простых множителей и переменных, после чего осуществить сокращение:

— 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 · 3 · 3 · a · a · a · a · a · b · b · c · z 2 · 3 · a · a · b · b · c · c · c · c · c · c · c · z = = — 3 · 3 · a · a · a 2 · c · c · c · c · c · c = — 9 · a 3 2 · c 6

Однако, более рациональным способом будет запись решения в виде выражения со степенями:

— 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 3 3 · a 5 · b 2 · c · z 2 · 3 · a 2 · b 2 · c 7 · z = — 3 3 2 · 3 · a 5 a 2 · b 2 b 2 · c c 7 · z z = = — 3 3 — 1 2 · a 5 — 2 1 · 1 · 1 c 7 — 1 · 1 = · — 3 2 · a 3 2 · c 6 = · — 9 · a 3 2 · c 6 .

Ответ: — 27 · a 5 · b 2 · c · z 6 · a 2 · b 2 · c 7 · z = — 9 · a 3 2 · c 6

Когда в числителе и знаменателе алгебраической дроби имеются дробные числовые коэффициенты, возможно два пути дальнейших действий: или отдельно осуществить деление этих дробных коэффициентов, или предварительно избавиться от дробных коэффициентов, умножив числитель и знаменатель на некое натуральное число. Последнее преобразование проводится в силу основного свойства алгебраической дроби (про него можно почитать в статье «Приведение алгебраической дроби к новому знаменателю»).

Задана дробь 2 5 · x 0 , 3 · x 3 . Необходимо выполнить ее сокращение.

Решение

Возможно сократить дробь таким образом:

2 5 · x 0 , 3 · x 3 = 2 5 3 10 · x x 3 = 4 3 · 1 x 2 = 4 3 · x 2

Попробуем решить задачу иначе, предварительно избавившись от дробных коэффициентов – умножим числитель и знаменатель на наименьшее общее кратное знаменателей этих коэффициентов, т.е. на НОК ( 5 , 10 ) = 10 . Тогда получим:

2 5 · x 0 , 3 · x 3 = 10 · 2 5 · x 10 · 0 , 3 · x 3 = 4 · x 3 · x 3 = 4 3 · x 2 .

Ответ: 2 5 · x 0 , 3 · x 3 = 4 3 · x 2

Когда мы сокращаем алгебраические дроби общего вида, в которых числители и знаменатели могут быть как одночленами, так и многочленами, возможна проблема, когда общий множитель не всегда сразу виден. Или более того, он попросту не существует. Тогда для определения общего множителя или фиксации факта о его отсутствии числитель и знаменатель алгебраической дроби раскладывают на множители.

Задана рациональная дробь 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 . Необходимо ее сократить.

Решение

Разложим на множители многочлены в числителе и знаменателе. Осуществим вынесение за скобки:

2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · ( a 2 + 14 · a + 49 ) b 3 · ( a 2 — 49 )

Мы видим, что выражение в скобках возможно преобразовать с использованием формул сокращенного умножения:

2 · b 2 · ( a 2 + 14 · a + 49 ) b 3 · ( a 2 — 49 ) = 2 · b 2 · ( a + 7 ) 2 b 3 · ( a — 7 ) · ( a + 7 )

Хорошо заметно, что возможно сократить дробь на общий множитель b 2 · ( a + 7 ) . Произведем сокращение:

2 · b 2 · ( a + 7 ) 2 b 3 · ( a — 7 ) · ( a + 7 ) = 2 · ( a + 7 ) b · ( a — 7 ) = 2 · a + 14 a · b — 7 · b

Краткое решение без пояснений запишем как цепочку равенств:

2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · b 2 · ( a 2 + 14 a + 49 ) b 3 · ( a 2 — 49 ) = = 2 · b 2 · ( a + 7 ) 2 b 3 · ( a — 7 ) · ( a + 7 ) = 2 · ( a + 7 ) b · ( a — 7 ) = 2 · a + 14 a · b — 7 · b

Ответ: 2 · a 2 · b 2 + 28 · a · b 2 + 98 · b 2 a 2 · b 3 — 49 · b 3 = 2 · a + 14 a · b — 7 · b .

Случается, что общие множители скрыты числовыми коэффициентами. Тогда при сокращении дробей оптимально числовые множители при старших степенях числителя и знаменателя вынести за скобки.

Дана алгебраическая дробь 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 . Необходимо осуществить ее сокращение, если это возможно.

Решение

На первый взгляд у числителя и знаменателя не существует общего знаменателя. Однако, попробуем преобразовать заданную дробь. Вынесем за скобки множитель х в числителе:

1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2

Теперь видна некая схожесть выражения в скобках и выражения в знаменателе за счет x 2 · y . Вынесем за скобку числовые коэффициенты при старших степенях этих многочленов:

x · 1 5 — 2 7 · x 2 · y 5 · x 2 · y — 3 1 2 = x · — 2 7 · — 7 2 · 1 5 + x 2 · y 5 · x 2 · y — 1 5 · 3 1 2 = = — 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10

Теперь становится виден общий множитель, осуществляем сокращение:

— 2 7 · x · — 7 10 + x 2 · y 5 · x 2 · y — 7 10 = — 2 7 · x 5 = — 2 35 · x

Ответ: 1 5 · x — 2 7 · x 3 · y 5 · x 2 · y — 3 1 2 = — 2 35 · x .

Сделаем акцент на том, что навык сокращения рациональных дробей зависит от умения раскладывать многочлены на множители.

Источник

Сокращение обыкновенных дробей

О чем эта статья:

Что такое «сокращение дробей»

Математика любит точность и краткость: лохматыми громоздкими числами ее расположение не заслужить. Поэтому, следуя негласному правилу, сокращайте все, что можно сократить.

Сократить дробь — значит разделить ее числитель и знаменатель на их общий делитель. Общий делитель должен быть положительным и не равен нулю и единице.

В результате сокращения вы получаете новую дробь, равную исходной дроби. Такие дроби равны по основному свойству:

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число — получится дробь, равная данной.

С основным свойством дроби знакомятся в 5 классе, но встречаться оно будет до самого окончания школы. Поэтому запоминаем, как выглядит основное свойство дроби в виде буквенных выражений:

=

=

где a, b, m — натуральные числа.

Графически сокращение дробей обычно записывается вот так:

Числитель и знаменатель зачеркиваются черточками. В этом примере числитель — 8, знаменатель — 36. Справа над ними записывают результаты деления числителя и знаменателя на их общий делитель. Общий делить 8 и 36 — 4. Это число не нужно записывать.

Пример 1. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 3.

= =

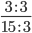
Сокращение выполнено: =

Пример 2. Сократим обыкновенную дробь

Разделим числитель и знаменатель на общий делитель 2.

= =

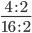
Сокращение выполнено: =

Приведение дробей к несократимому виду

Смысл сокращения дробей в том, чтобы в результате сокращения в числителе и знаменателе оказались наименьшие из возможных чисел.

Так, в результате сокращения в примере 2, мы из дроби получили дробь

Выходит, что дробь выдержит еще одно сокращение и придет к виду

Сокращая дробь, стремитесь в итоге получить несократимую дробь.

Разделите числитель и знаменатель дроби на их НОД (наибольший общий делитель). Так вы приведете дробь к несократимому виду.

— несократимая дробь, так как по свойствам НОД мы знаем, что:

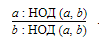
a : НОД(a, b) и b : НОД(a, b) — взаимно простые числа.

Два целых числа a и b называются взаимно простыми, если их наибольший общий делитель равен единице, НОД(a, b) = 1.

• Несократимые дроби: ; ; ;

Пример 3. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 12

Найдем частное: 12 : 12 = 1

= =

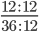
Сокращение выполнено: =

Пример 4. Приведите обыкновенную дробь к несократимому виду

Найдем НОД числителя и знаменателя. НОД = 5

Найдем частное: 15 : 5 = 3

= =

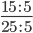
Сокращение выполнено: =

Правило сокращения дробей

Чтобы без труда сокращать любую обыкновенную дробь, запомните правило.

Выполняйте сокращение дробей по следующему алгоритму:

1. Найдите НОД числителя и знаменателя дроби.
2. Разделите числитель и знаменатель дроби на НОД.

В 6 классе каждая вторая задачка — с дробями. Чтобы легко управляться с ними и уметь сокращать любые числа, нужно хорошо потренироваться. Давайте разберем еще несколько примеров сокращения обыкновенных дробей.

Чтобы легко сокращать дроби, нужно уметь быстро находить НОД числителя и знаменателя. Для этого неплохо бы знать таблицу умножения и уметь раскладывать числа на простые множители.

• Например, дана дробь

Чтобы найти НОД числителя и знаменателя, разложим числа на простые множители.
36 = 2 * 2 * 3 * 3
84 = 2 * 2 * 3 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 = 12.
НОД 36 и 84 = 12.

Пример 5. Сократите дробь

Разложим числа в числителе и знаменателе на множители.
135 = 9 * 3 * 5
180 = 9 * 2 * 2 * 5

Мысленно убираем все общие множители и перемножаем оставшиеся.

= =

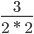
Сокращение выполнено: =

Пример 6. Сократите обыкновенную дробь

Найдем НОД числителя и знаменателя. НОД = 9

= =

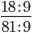
Сокращение выполнено: =

Дробь можно сократить, последовательно сокращая числитель и знаменатель на общий делитель. Такой способ подходит, если в числителе и знаменателе стоят крупные числа, и вы не уверены в подобранном НОД.

Пример 6. Сократите дробь:

= = =

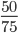
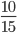
Сокращение выполнено: =

Пример 7. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

168 = 2 * 2 * 2 * 3 * 7

240 = 2 * 2 * 2 * 2 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 2 * 3 = 24

НОД 168 и 240 равен 24

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 168 : 24 = 7

= =

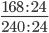
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

360 = 2 * 2 * 2 * 3 * 3 * 5

540 = 2 * 2 * 3 * 3 * 3 * 5

Перемножаем все общие множители между собой 2 * 2 * 3 * 3 * 5 = 180

НОД 360 и 540 равен 180

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 360 : 180 = 2

= =

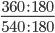
Сокращение выполнено: =

Пример 8. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

420 = 2 * 2 * 3 * 5 * 7

2520 = 2 * 2 * 2 * 3 * 3 * 5 * 7

Перемножаем все общие множители между собой 2 * 2 * 3 * 5 * 7 = 420

НОД 420 и 2520 равен 420

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 420 : 420 = 1

= =

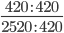
Сокращение выполнено. Дробь приведена к несократимому виду: =

Пример 9. Сократите дробь

Найдем НОД, разложив числитель и знаменатель на простые множители.

1575 = 3 * 3 * 5 * 5 * 7

3450 = 2 * 3 * 5 * 5 * 23

Перемножаем все общие множители между собой 3 * 5 * 5 = 75

НОД 1575 и 3450 равен 72

Следующим шагом разделим числитель и знаменатель дроби на их наибольший общий делитель: 1575 : 75 = 21

= =

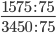
Сокращение выполнено. Дробь приведена к несократимому виду: =

Иногда разложение на простые множители занимает немало времени, особенно если раскладываемые числа большие, как в двух предыдущих примерах. Чтобы быстро разложить любое число на простые множители, можно обратиться к онлайн-калькулятору — в интернете их много. Воспользуйтесь одним из них.

Если времени совсем не хватает — можно использовать онлайн-калькулятор и для нахождения НОД. Однако не стоит постоянно прибегать к калькулятору для решения задач, пока вы не научитесь уверенно и быстро вычислять сами.

Источник
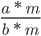
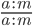
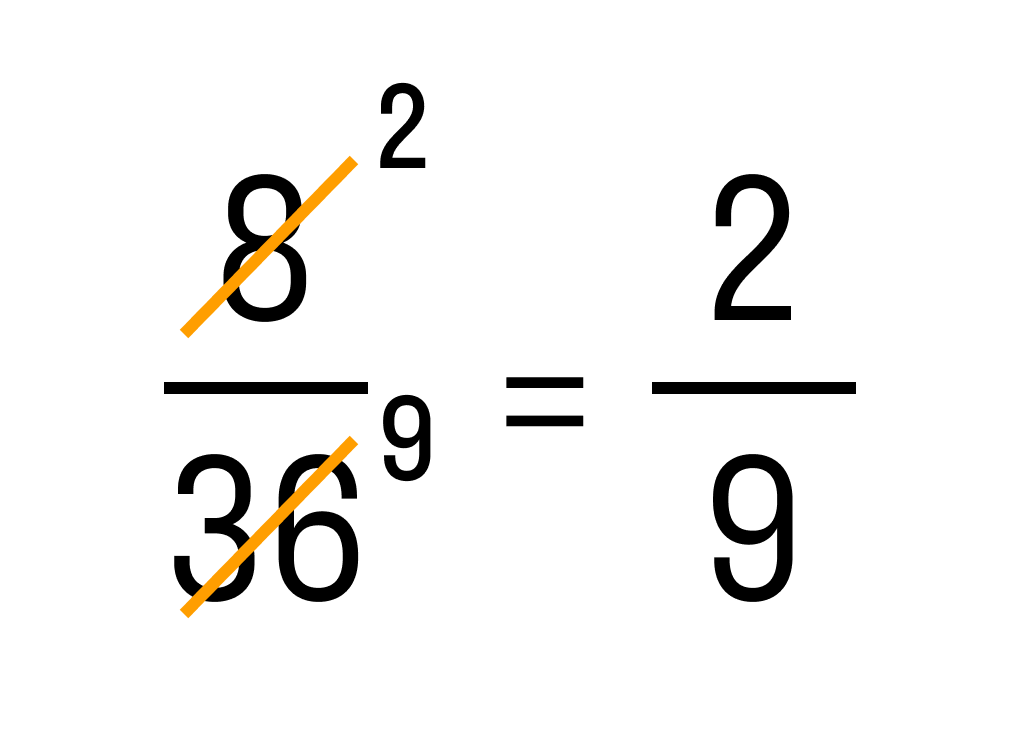
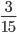
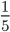
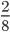
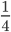
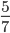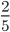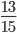