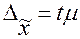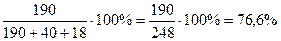ОСНОВНЫЕ СПОСОБЫ ФОРМИРОВАНИЯ ВЫБОРОЧНОЙ СОВОКУПНОСТИ
Поможем написать любую работу на аналогичную тему
Результаты выборочного наблюдения, размер ошибки выборки и методы ее определения зависят от способа и метода формирования выборочной совокупности.
Существует два МЕТОДА ОТБОРА единиц из генеральной совокупности в выборочную: бесповторный и повторный.
БЕСПОВТОРНЫМ называется такой отбор, при котором попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор.
При ПОВТОРНОМ ОТБОРЕ попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность.
МЕТОД ОТБОРА определяет возможность продолжения участия отобранной единицы в процедуре отбора.
СПОСОБ ОТБОРА – это конкретный механизм или процедура выборки единиц из генеральной совокупности.
Различают четыре вида (способа) формирования выборочной совокупности:
Ø случайный (собственно случайный);
Ø серийный (гнездовой).
СЛУЧАЙНЫЙ ОТБОР. При этом способе отбора единицы из генеральной
совокупности выбираются наугад, без каких- либо элементов системности.
Технически собственно случайный отбор производится методом жеребьевки или
по таблице случайных чисел.
Собственно – случайный отбор может быть как повторным, так и бесповторным.
МЕХАНИЧЕСКИЙ ОТБОР . Применяется в тех случаях, когда генеральная
совокупность, каким – либо образом упорядочена ( по алфавиту, по табельным
номерам, по адресам и т. п.). Для проведения такой выборки устанавливается
пропорция отбора, например, каждая десятая единица, каждая 50-я единица.
ТИПИЧЕСКАЯ ВЫБОРКА используется в тех случаях, когда единицы генеральной совокупности можно разбить на несколько типических групп. При обследовании населения такими группами могут быть социальные группы, возрастные или образовательные; при обследовании предприятий – группы по формам собственности, по отраслям и т. д.
Отбор единиц для исследования производится собственно случайным или механическим способом.
СЕРИЙНЫЙ ОТБОР. Отбору подлежат не отдельные единицы совокупности, а целые группы (гнезда, серии), отобранные собственно случайным или механическим способом.
Источник
Способы формирования выборочной совокупности
В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.
Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.
Существуют следующие способы отбора единиц из генеральной совокупности:
1) индивидуальный отбор — в выборку отбираются отдельные единицы;
2) групповой отбор — в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор — это комбинация индивидуального и группового отбора.
Способы отбора определяются правилами формирования выборочной совокупности.
Выборка может быть:
- собственно-случайная состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.
- механическая состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке — каждая 20-я единица (1:0,05) и т.д. Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица.
- типическая – при которой генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность;
- серийная — при которой генеральную совокупность делят на одинаковые по объему группы — серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию;
- комбинированная — выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.
В статистике различают следующие способы отбора единиц в выборочную совокупность:
- одноступенчатая выборка — каждая отобранная единица сразу же подвергается изучению по заданному признаку (собственно-случайная и серийная выборки);
- многоступенчатая выборка — производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы (типическая выборка с механическим способом отбора единиц в выборочную совокупность).
Источник
Основные способы формирования выборочной совокупности
Достоверность рассчитанных по выборочным данным характеристик в значительной степени определяется репрезентативностью выборочной совокупности, которая в свою очередь, зависит от способа отбора единиц из генеральной совокупности. В каждом конкретном случае в зависимости от целого ряда условий, а именно сущности исследуемого явления, объема совокупности, вариации и распределения наблюдаемых признаков, материальных и трудовых ресурсов, выбирают наиболее предпочтительную систему организации отбора, которая определяется видом, методом и способом отбора.
По виду различают:
· индивидуальный (при индивидуальном отборе в выборочную совокупность отбираются отдельные единицы генеральной совокупности)
· групповой (группы единиц)
· комбинированный (сочетание группового и индивидуального отбора)
Метод отбора определяет возможность продолжения участия отобранной единицы в процедуре отбора.
· бесповторный (попавшая в выборку единица не возвращается в совокупность, из которой осуществляется дальнейший отбор.
· повторный (попавшая в выборку единица после регистрации наблюдаемых признаков возвращается в исходную (генеральную) совокупность для участия в дальнейшей процедуре отбора. При этом методе отбора объем генеральной совокупности остается неизменным, что обуславливает постоянную вероятность попадания в выборку всех единиц совокупности.
Способ отбора определяет конкретный механизм или процедуру выборки единиц из генеральной совокупности. В практике выборочных обследований наибольшее распространение получили следующие виды выборки:
Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности.
Технически собственно-случайный отбор проводят методом жеребьевки или по таблице случайного отбора.
Собственно-случайный отбор может быть как повторным, так и бесповторным.
Механическая выборкаприменяется в том случаях, когда генеральная совокупность каким-либо образом упорядочена, т. е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т. п.)
Для проведения механической выборки устанавливается пропорция отбора, которая определяется соотнесением объемов выборочной и генеральной совокупностей. Так, если из совокупности в 500 000 единиц предполагается получить 2 % выборку, т. е. отобрать 10 000 единиц, то пропорция отбора составит
Отбор единиц осуществляется в соответствии с установленной пропорцией через равные интервалы. Например при 2 % выборке отбирается каждая 50-я единица, при 5% выборке каждая 20-я единица и т. д.
Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или его завышением (если из каждого интервала регистрируется последние значение). Поэтому целесообразно отбор начинать с середины первого интервала, например при 5 % выборке отобрать 10, 30, 50, 70 и с таким же интервалом последующие единицы.
Опасность систематической ошибки при механической выборке также может появиться вследствие случайного совпадения выбранного интервала и циклических закономерностей в расположении единиц генеральной совокупности. Так, при Всесоюзной переписи населения 1989 г. в ходе 25 % выборочного обследования семей имела место опасность попадания в выборку квартир только одного типа (например, только однокомнатных или только трехкомнатных), так как на лестничных площадках многих типовых домов располагаются именно по 4 квартиры. Чтобы избежать систематической ошибки, в каждом новом подъезде счетчик менял начало отбора.
Для определения средней ошибки механической выборки используется формула средней ошибки при собственно-случайном бесповторном отборе.
Типический отбор. Этот способ отбора используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. При обследованиях населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы, при обследовании предприятий — отрасль и подотрасль, форма собственности и т. п.. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки, которая в этом случае определяется только внутригрупповой вариацией.
Отбор единиц в типическую группировку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака.
При выборке, пропорциональной объему типических групп, число единиц, подлежащих отбору из каждой группы, определяется следующим образом:
где 
-объем i — группы
ni — объем выборки из i — группы
Средняя ошибка такой выборки находится по формулам:
(повторный отбор)
(бесповторный отбор)
где 
— средняя из внитригрупповых дисперсий
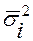
При выборке, пропорциональной дифференциации признака, число наблюдений по каждой группе рассчитывается по формуле
,
где si — средняя из внутригрупповых дисперсий
Средняя ошибка такого отбора определяется следующим образом
(повторный отбор)
(бесповторный отбор)
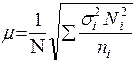
Отбор, пропорциональный дифференциации признака, дает лучшие результаты, однако на практике его применение затруднено вследствие трудности получения сведений о вариации до проведения выборочного наблюдения.
Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном либо механическом отборе серий, внутри которых производится сплошное обследование единиц.
Поскольку внутри групп (серий) обследуются все без исключения единицы, средняя ошибка серийной выборки (при отборе равновеликих серий) зависит от величины только межгрупповой (межсерийной) дисперсии и определяется по следующим формулам:
(повторный отбор)
(бесповторный отбор)
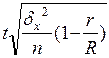
где r — число отобранных серий
R — общее число серий
Межгрупповую дисперсию вычисляют следующим образом:
где — средняя i-й серии
— общая средняя по всей выборочной совокупности.
Комбинированный отбор. В практике статистических обследований помимо рассмотренных выше способов отбора применяется и их комбинация. Так, например, можно комбинировать типическую и серийную выборки, когда серии отбираются в установленном порядке из нескольких типических групп. Возможна также комбинация серийного и собственно-случайного отборов, при которой отдельные единицы отбираются внутри серии в собственно-случайном порядке. Ошибка такой выборки определяется ступенчатостью отбора.
Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом более мелкие и так до тех пор пока не будут отобраны те единицы, которые подвергаются обследованию.
В отличии от многоступенчатой многофазная выборка предполагает сохранение одной и той же единицы отбора на всех этапах его проведения, при этом отобранные на каждой стадии единицы подвергаются обследованию (на каждой последующей стадии отбора программа обследования расширятся).
Исходя из вышеизложенного приведем формулы предельной ошибки выборки для наиболее часто используемых на практике способов формирования выборочной совокупности.
Предельная ошибка выборки для некоторых способов формирования выборочной совокупности 
| повторный | бесповторный | |||
| для средней | для доли | для средней | для доли | |
| 1. Собственно-случайная и механическая |  |  |  |  |
| 2. Типическая (при пропорциональном объему групп отборе) |  |  |  |  |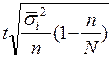
| 3. Серийная (гнездовая) |  |  |  |  |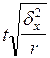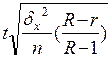
Практические задания
Задача 1
На основе данных, приведенных в следующей таблице о численности городского и сельского населения (млн. чел.), исчислить показатели, характеризующие динамику численности и структуру.
| Год | Все население, млн.чел. | В том числе |
| городское | сельское | |
| 129,9 | 80,6 | 49,3 |
| 133,6 | 88,9 | 44,7 |
| 138,1 | 96,1 | 42,0 |
| 142,5 | 102,4 | 40,1 |
| 147,7 | 108,8 | 38,9 |
| 148,3 | 108,3 | 40,0 |
| 146,3 | 107,1 | 39,2 |
| 143,2 | 104,8 | 38,4 |
| 142,9 | 105,4 | 37,5 |
| 146,5 | 108,6 | 37,9 |
| 146,8 | 109,5 | 37,3 |
Решение.
Абсолютный прирост на цепной основе вычисляется по формуле 
, 
.
Абсолютный прирост на базисной основе вычисляется по формуле 
, .
Темп роста на цепной основе вычисляется по формуле 
, .
Темп роста на базисной основе вычисляется по формуле 
, .
Темп прироста на цепной основе вычисляется по формуле 
.
Темп прироста на базисной основе вычисляется по формуле 
.
Абсолютное значение 1% прироста 
, 
.
Вычисленные по данным формулам показатели сведены в таблицу.
| Все население, млн.чел. | Абсолютный прирост, млн.чел. | Темп роста, % | Темп прироста, % | Абсолютное содержание 1 % прироста, млн.чел. | |||
| Базисный | Цепной | Базисный | Цепной | Базисный | Цепной | ||
| 129,9 | — | — | — | — | — | — | — |
| 133,6 | 3,7 | 3,7 | 102,8 | 102,8 | 2,8 | 2,8 | 1,299 |
| 138,1 | 8,2 | 4,5 | 106,3 | 103,4 | 6,3 | 3,4 | 1,336 |
| 142,5 | 12,6 | 4,4 | 109,7 | 103,2 | 9,7 | 3,2 | 1,381 |
| 147,7 | 17,8 | 5,2 | 113,7 | 103,6 | 13,7 | 3,6 | 1,425 |
| 148,3 | 18,4 | 0,6 | 114,2 | 100,4 | 14,2 | 0,4 | 1,477 |
| 146,3 | 16,4 | -2 | 112,6 | 98,7 | 12,6 | -1,3 | 1,483 |
| 143,2 | 13,3 | -3,1 | 110,2 | 97,9 | 10,2 | -2,1 | 1,463 |
| 142,9 | -0,3 | 110,0 | 99,8 | 10,0 | -0,2 | 1,432 | |
| 146,5 | 16,6 | 3,6 | 112,8 | 102,5 | 12,8 | 2,5 | 1,429 |
| 146,8 | 16,9 | 0,3 | 113,0 | 100,2 | 13,0 | 0,2 | 1,465 |
Вычислим показатели структуры городского и сельского населения за каждый год.
ОВС = Часть совокупности · 100% / Итог совокупности
Данные расчетов сведем в таблицу.
| Год | Все население, % | В том числе |
| городское | сельское | |
| 100,0 | 62,0 | 38,0 |
| 100,0 | 66,5 | 33,5 |
| 100,0 | 69,6 | 30,4 |
| 100,0 | 71,9 | 28,1 |
| 100,0 | 73,7 | 26,3 |
| 100,0 | 73,0 | 27,0 |
| 100,0 | 73,2 | 26,8 |
| 100,0 | 73,2 | 26,8 |
| 100,0 | 73,8 | 26,2 |
| 100,0 | 74,1 | 25,9 |
| 100,0 | 74,6 | 25,4 |
Таким образом, доля городского населения ежегодно увеличивается.
Задача 2
По данным таблицы определите средний возраст, моду, медиану и показатели вариации возраста безработных.
| Возраст, лет | Число безработных, % |
| 15 – 19 | 13,6 |
| 20 – 24 | 18,6 |
| 25 – 29 | 19,1 |
| 30 – 49 | 36,5 |
| 50 – 54 | 5,1 |
| 55 – 59 | 4,0 |
| 60– 65 | 3,1 |
| Итого |
Решение.
Определим средний возраст безработного по формуле средней арифметической взвешенной, в качестве вариант используем середины интервалов: 
лет.
Найдем моду, для этого сначала найдем модальный интервал, т.е. интервал с наибольшей частотой. Чтобы найти конкретное значение моды, необходимо использовать формулу
где xМо — нижняя граница модального интервала; iМо — величина модального интервала; fМо — частота модального интервала; fМо-1 — частота интервала, предшествующего модальному; fМо+1 — частота интервала, следующего за модальным.
лет
Найдем медиану, для этого сначала найдем медианный интервал, т.е. первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений (совпадает с модальным).
Численное значение медианы обычно определяют по формуле
где: 
— нижняя граница медианного интервала;
— величина медианного интервала;
— накопленная частота интервала, предшествующего медианному;
— частота медианного интервала;
лет
| Возраст, лет | Число безработных, %,  |  | |  |  |
| 15 – 19 | 13,6 | 231,2 | 251,159104 | 3415,763814 | |
| 20 – 24 | 18,6 | 409,2 | 117,679104 | 2188,831334 | |
| 25 – 29 | 19,1 | 515,7 | 34,199104 | 653,2028864 | |
| 30 – 49 | 36,5 | 39,5 | 1441,75 | 44,249104 | 1615,092296 |
| 50 – 54 | 5,1 | 265,2 | 366,799104 | 1870,67543 | |
| 55 – 59 | 583,319104 | 2333,276416 | |||
| 60– 65 | 3,1 | 62,5 | 193,75 | 879,241104 | 2725,647422 |
| Итого | 3284,8 | 2276,645728 | 14802,4896 |
Дисперсия 
.
Среднее квадратическое отклонение 
лет
Коэффициент вариации 
, т.к. коэффициент вариации больше 33%, то исследуемую совокупность нельзя считать однородной.
Задача 3
На предприятии работают 190 менеджеров, 40 курьеров и 18 руководителей. Рассчитать ОВС (относительные величины структуры).
Решение.
ОВС = Часть совокупности · 100% / Итог совокупности
ОВС менеджеры = 
ОВС курьеры = 
ОВС руководители = 
Список литературы
1. Елисеева И.А., Юзбашев М.М. Общая теория статистики. — М.: Финансы и статистика, 2016.
2. Ефимова М.Р., Бычкова С.Г. Социальная статистика: Учебное пособие. — М.: Финансы и статистика, 2012.
3. Общая теория статистики: статистическая методология в изучении коммерческой деятельности. Под ред. О.Э. Бащина. — М.: Финансы и статистика, 2013.
Источник
