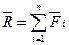wiki.eduVdom.com
Инструменты пользователя
Инструменты сайта
Боковая панель
Теория вероятностей и математическая статистика 
Строительная механика для строительных специальностей
Матанализ. Дифференциальное и интегральное исчисление
economics
Теоретическая механика. Статика:
Контакты
Графическое определение равнодействующей сходящихся сил
Теорема 1. Равнодействующая системы сходящихся сил существует, приложена в центре системы, равна их геометрической (векторной) сумме и изображается замыкающей стороной силового многоугольника.
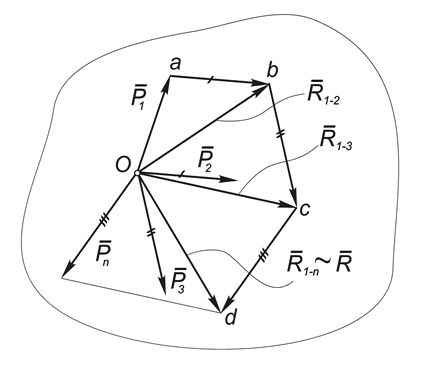
Для доказательства рассмотрим систему сходящихся сил, приложенных в центре О : (Рис.1).
По аксиоме параллелограмма две первых силы этой системы можно заменить равнодействующей $\vec
Затем точно так же можно найти равнодействующую силы $\vec
Продолжая эту процедуру, мы найдем равнодействующую всей системы:
, которая изображается замыкающей стороной силового многоугольника Oabcd.
Отметим, что в общем случае этот многоугольник будет пространственной фигурой, поэтому графический метод определения равнодействующей удобен только для плоской системы сил.
Универсальным для определения равнодействующей системы сходящихся сил является аналитический метод, к рассмотрению которого мы и переходим.
Источник
Графический способ определения равнодействующей сходящихся сил на плоскости.
Пусть задана произвольная система сходящихся сил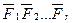 
, приложенных к твердому телу.
Перенесем эти силы как скользящие векторы в точку пересечения линий их действия. Затем, пользуясь аксиомой о параллелограмме сил, найдем равнодействующую этих сил. Равнодействующая такой системы может быть определена графически и аналитически.
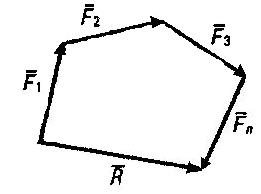
Графически сложение двух сходящихся сил производится по правилу параллелограмма, причем 
. Затем по правилу параллелограмма складываем силы 
и 
, и получаем их равнодействующую 
. Продолжая процесс, получим 
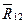
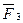
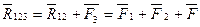
Процесс последовательного применения правила параллелограмма приводит к построению многоугольника из заданных сил. В силовом многоугольнике конец одной из сил служит началом другой. Равнодействующая сила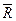 
в силовом многоугольнике соединяет начало первой силы с концом последней, т.е. изображается замыкающей силового многоугольника.
Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской — плоской.
Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпадать с началом первой силы.
Такой силовой многоугольник называют замкнутым.
Получено условие равновесия системы сходящихся сил: для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая сила равнялась нулю 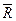= 0. Это условие является геометрическим.
Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.
Источник
Техническая механика. Шпаргалка
Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.
Оглавление
- 1. Аксиомы и понятие силы статики
- 2. Связи и реакции связей
- 3. Определение равнодействующей геометрическим способом
- 4. Определение равнодействующей аналитическим способом
- 5. Пара сил. Момент силы
Приведённый ознакомительный фрагмент книги Техническая механика. Шпаргалка предоставлен нашим книжным партнёром — компанией ЛитРес.
4. Определение равнодействующей аналитическим способом
Проекция сил на ось определяется отрезком оси, отсекаемой перпендикулярами, опущенными на ось из начала и конца вектора.
Величина проекции силы на ось равна произведению модуля силы на косинус угла между вектором силы и положительным направлением сил. Проекция имеет знак: положительный при одинаковом направлении вектора силы и оси и отрицательный при направлении в сторону отрицательной полуоси.
Проекция силы на две взаимно перпендикулярные оси.
Величина равнодействующей равна векторной (геометрической) сумме векторов системы сил. Определим равнодействующую аналитическим способом. Выберем систему координат, определим проекции всех заданных векторов на эти оси. Складываем проекции всех векторов на оси х и у.
Модуль (величину) равнодействующей можно определить по известным проекциям:
Направление вектора равнодействующей можно определить по величинам и знакам косинусов углов, образуемых равнодействующими с осями координат:
Плоская система сходящихся сил находится в равновесии, если алгебраическая сумма проекций всех сил системы на любую ось равна нулю.
Система уравнений равновесия плоской системы сходящихся сил:
При решении задач координатные оси выбирают так, чтобы решение было наиболее простым. При этом желательно, чтобы хотя бы одна неизвестная сила совпадала с осью координат.
Источник
Рассматриваем равновесие шарнира В.
Алгоритм и пример практического занятия №1
Тема: Определение реакций идеальных связей аналитическим и графическим способом.
Знать: способы сложения двух сил и разложение силы на составляющие, геометрический и аналитический способы определения равнодействующей силы, условия равновесия плоской сходящейся системы сил.
Уметь: определять равнодействующую системы сил, решать задачи на равновесие геометрическим и аналитическим способом, рационально выбирая координатные оси.
АЛГОРИТМ ВЫПОЛНЕНИЯ ПРАКТИЧЕСКОГО ЗАНЯТИЯ № 1
Указывают точку, равновесие которой рассматривается.
Ø В задачах такой точкой является центр тяжести тела или точки пересечения всех стержней и нитей.
Ø 2 Прикладывают к рассматриваемой точке активные силы.
Активными силами являются собственный вес тела или вес груза, которые направлены к центру тяжести земли. При наличии блока вес груза действует на рассматриваемую точку вдоль нити. Направление действия этой силы устанавливается из чертежа. Вес тела принято обозначать G
Мысленно отбрасывают связи, заменяя их действия реакциями связей.
Ø При замене связей реакциями следует помнить, что реакция плоскости направлена по нормали (перпендикуляру)к ней в точке контакта, а реакции стержня и нити – по их осям. Реакцию нити и стержня принято называть усилиями.
Выбираем положение прямоугольной системы координат
Ø Начало координат совмещают с точкой, равновесие которой рассматривается.
5 Составляют уравнения равновесия вида: ΣFx = 0; ΣFу = 0
Ø Напомним, что проекцией силы на ось является произведение модуля (величины) этой силы на косинус угла между направлением силы и направлением оси. Если угол между направлениями силы и оси острый, то перед величиной проекции ставится знак «плюс», т.е. сила и ось направлены в одну сторону, если они направлены в противоположные стороны, то ставится знак «минус».
Выполняем проверку решения
Ø Аналитическим или графическим способом.
Фонарь весом 80 Н подвешен на кронштейне АВС, укреплённом на вертикальной стене (рис. 2-а). Определить усилия возникшие в горизонтальном стержне СВ и наклонной тяге АВ после подвески фонаря, если СВ=1м и АВ= 1,2м. Соединения в точках А, В и С – шарнирные.
|
2-а
Дано: АВ-1,2м
 |
Рассматриваем равновесие шарнира В.
2 Освобождаем шарнир В от связей и изображаем дейс
твующие на него активные силы и реакции связей
 |
2-б У 3 Выбираем систему координат и составляем уравнение
RA для системы сил, действующих на шарнир В
RС Х ΣFУ = 0 RА cos β — G = 0 (2)
G4. Определяем реакции стержней, решая уравнения (1) и
Из уравнения (2): RА = G / cos β
По теореме Пифагора находим АС: АС = √АВ 2 –ВС 2 = √1,2 2 –1 2 = 0,664 м.
cos β = 0,664 / 1,2 , тогда RА = ( 80 · 1,2) / 0,664 = 144,5 Н
Из уравнения (1): — RС = RА cos α ; RС = 144,5 · (1/ 1,2) = — 120,5 Н
Знак минус перед значением RС указывает на то, что направление реакции в
противоположную сторону, т. е. к шарниру В.
5.Правильность полученных результатов можно проверить, решая задачуграфически.
Для решения задачи графическим способом выбирают масштаб (например 1:20) и строят кронштейн АВС. Для чего из произвольной точки С (рис. 2-в) проводим горизонтальную и вертикальную линии. На горизонтальной линии отложим отрезок СВ= (1м=1000мм/20)=50 мм. При помощи циркуля из точки В отложим отрезок АВ=60 мм. Построенный треугольник АВС изображает в масштабе данный в условии задачи кронштейн. (2-в)
|
Вес фонаря G =80 Н, действующий на кронштейн вертикально вниз, изобразим
отрезком ВД=20 мм.
Значит масштаб построения для сил : М = G / ВД = 80 Н / 20 мм = 4 Н/мм ( 4 Н в 1 мм ). Благодаря тому, что в точках А, В и С кронштейна соединения шарнирные, стержни, находясь под действием веса фонаря, либо сжимаются, либо растягиваются. Иными словами, искомые усилия действуют вдоль стержней.
Изобразим направление действия искомых сил линиями Аа и Сс, пересекающимися в точке В – точка приложения к кронштейну веса фонаря . Из точки Д (конца вектора G ) проводим прямые ДМ параллельно Аа. В получившемся параллелограмме ВМДL стороны ВМ и ВL изображают силы RА и RС , действующие соответственно на тягу АВ и стержень ВС. При помощи масштабной линейки измерим отрезки ВМ и ВL : ВМ = 36 мм, ВL = 30 мм
RА = МF · ВМ = 4 Н/ мм · 36 мм = 144 Н
RС = МF · В L = 4 Н/ мм · 30 мм = 120 Н
Графическое решение подтверждает правильность первого решения.
Примечание: Если при решении реакция связи окажется отрицательной, значит, вектор силы направлен в противоположную сторону.
Цель: Научиться определять вероятные направления реакций связей.
| Рисунок: | Дано: _______________________________________ ________________________________________ ________________________________________ Определить усилия в стержнях: _______________________________________ _______________________________________ |
| Расчётная схема: | 1 Выбираем объект, равновесие которого рассматриваем: точка___________________ 2 Освобождаем объект от связей и прикладываем к рассматриваемому объекту равновесия все активные ______________________________________и реактивные силы_______________________ _______________________________________ |
| 3 Проанализируем, полученную систему сил. Тело находится в равновесии под действием плоской системы сходящихся сил (линии их действия пересекаются в центре) — точка_____ 4Выбираем систему координат — проводим оси «Х» и «У» 5 Составляем уравнения равновесия вида: ΣFx = 0____________________________________________________________ ΣFу = 0___________________________________________________________ |
Решение уравнений:_____________________________________________________
Решив полученную систему уравнений, определяем усилия в стержнях (нитях).
6 Правильность полученных результатов можно проверить, решая задачуграфически:Выбираем масштаб М __________________, строим замкнутый многоугольник.
| Проверяем графическое построение по теореме синусов: _________________________________________ _________________________________________ _________________________________________ _________________________________________ _________________________________________ _________________________________________ _________________________________________ _________________________________________ _________________________________________ |
Графическое решение подтверждает правильность аналитического решения задачи.
 |
1.Какое движение является простейшим?__________________________________
2.Что называется материальной точкой?____________________________________
3.Что называется системой? ______________________________________________
4.Какое действие производят силы на реальные тела?_________________________
5.Какую систему сил образуют две силы, линии действия которых перекрещиваются?_______________________________________________________
6.Чему станет эквивалентна система сил, если к ней добавить уравновешивающую силу?__________________________________________________________________
7. При каком способе графического определения равнодействующей двух сил приходится выполнять меньшее число построений?__________________________
8. Почему силы действия и противодействия не могут взаимно уравновешиваться?______________________________________________________
9. К чему приложена реакция опоры?_______________________________________
10. В каком случае задача на равновесие плоской системы сходящихся сил является статически определимой?_________________________________________
Источник
