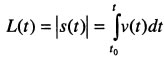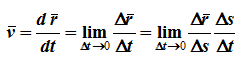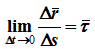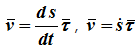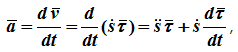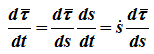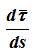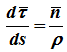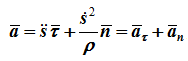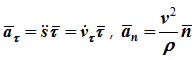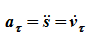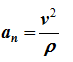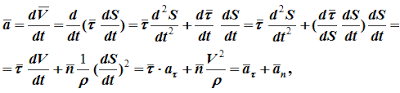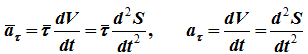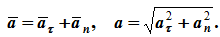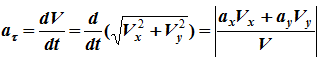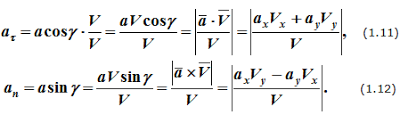При естественном способе задания движения точки ее касательное ускорение определяется второй

3) Скорость и ускорение точки при естественном способе задания движения.

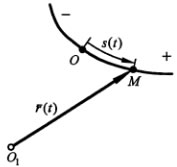
Если траектория точки известна (т.е. в некоторой системе отсчета определена графически, с помощью уравнения или другим образом), то задать движение точки можно естественным способом. Для этого необходимо: зафиксировать на трактории точку начала отсчета, выбрать положительное и отрицательное направления отсчета дуговой координаты и указать уравнение движения точки по траектории в виде S=S(t).

Скалярный параметр S в данном случае имеет смысл криволинейной (дуговой) координаты, модуль которой определяет текущее расстояние по траектории от начала отсчета (точки О) до подвижной точки М, а знак показывает, по какую сторону от начала отч=счета находится точка М на траектории.

Следует отметить, что уравнение движения в форме S=S(t) определяет текущее положение точки именно на траектории, при этом может быть установлена взаимно однозначная связь между значениями координаты S и радиус-вектором точки М в той системе отсчета, в которой определена в рассматриваемом случае траектория движения точки. Тогда радиус-вектор точки может быть представлен в виде функциональной зависимости от параметра S в виде r=r(S).

Модуль скорости, т.е. ее численное значение, при естественном способе задания движения точки определятся так: .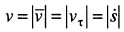

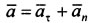
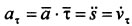
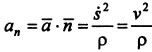
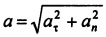
Ускорение составляет сумму касательной и нормальной составляющих: , где и . Следовательно: .

Дополнение: Значение пути —

Источник

Естественный способ задания движения точки

Введение

Естественный способ задания движения материальной точки применяется в тех случаях, когда траектория заранее известна. Например, точка движется внутри желоба в твердом теле. В этом случае мы, произвольным образом, выбираем некоторую неподвижную точку на траектории. Эту точку мы принимаем за начало отсчета. Далее мы произвольным образом выбираем положительное направление. Рассмотрим подвижную точку на траектории. Пусть – расстояние от точки до точки , измеренное вдоль дуги траектории. Введем криволинейную координату следующим образом. Если точка находится в положительном направлении относительно начала отсчета , то . Если точка находится в отрицательном направлении относительно начала отсчета , то . Тогда криволинейная координата однозначно определяет положение точки на траектории. При движении точки, координата изменяется со временем :
.

Таким образом, при естественном способе задания движения материальной точки, мы задаем следующие данные:
1) траекторию точки;
2) начало отсчета с указанием положительного и отрицательного направления отсчета;
3) криволинейную координату, как функцию от времени: .

Определение кинематических величин

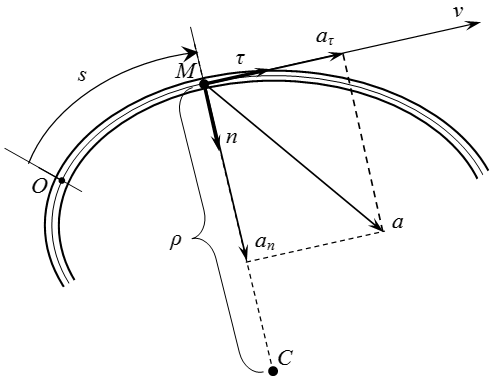
В начале мы должны определить геометрические характеристики траектории – касательную, главную нормаль и радиус кривизны.

По заданной траектории, для любого положения точки, мы можем определить единичный вектор , направленный по касательной к траектории; единичный вектор , направленный вдоль главной нормали (к центру кривизны) траектории и радиус кривизны траектории. Поскольку вектор можно направить по касательной двумя взаимно противоположными способами, то мы направим вектор вдоль направления, которое мы приняли за положительное. Вектор можно направить только одним способом – к центру кривизны траектории. Векторы и представляют собой два орта естественного трехгранника. В простых случаях, найти векторы , и радиус кривизны траектории можно геометрическим способом (см. пример решения задачи ниже). Как найти эти величины в более сложных случаях, указано на странице “Оси естественного трехгранника”. Там же приводится пример определения векторов , и радиуса кривизны траектории для винтовой линии.

После того, как мы определили орты естественного трехгранника , и радиус кривизны траектории , мы можем найти векторы скорости и ускорения точки . Выводы представленных ниже формул даны на странице “Кинематика материальной точки”.

Дифференцируя по , находим проекцию скорости на вектор :
.
Модуль скорости:
.
Вектор скорости:
.
Скорость, как и следовало, направлена по касательной к траектории. Если скорость направлена в положительном направлении, то
.
Если скорость направлена в отрицательном направлении, то
.

Дифференцируя по , находим тангенциальное ускорение (проекцию ускорения на вектор ):
.
Вектор тангенциального ускорения:
.
Нормальное ускорение:
.
Вектор нормального ускорения:
.
Вектор полного ускорения:
.
Модуль полного ускорения:
.

Пример решения задачи

Точка движется по дуге окружности радиуса по закону

( s – в метрах, t – в секундах), где – расстояние от до , измеренное вдоль дуги окружности. Определить скорость и ускорение точки в момент времени . Изобразить на рисунке векторы и , считая, что точка в этот момент находится в положении , а положительное направление отсчета – от к .

Определим положение точки в момент времени .
.
Пусть – центр окружности. Угол между векторами и :
.
По условию, положительное направление – от к , то есть слева направо. Поскольку , то точка расположена слева от точки .

Дифференцируя по , находим проекцию скорости на направление касательной к траектории:
.
В момент времени :
.
Поскольку , то вектор скорости направлен по касательной к траектории в сторону возрастания . Абсолютное значение (модуль) скорости:
.

Дифференцируя по , находим касательное ускорение точки:

.
В момент времени :
.
Поскольку , то вектор касательного ускорения направлен по касательной к траектории в сторону возрастания .

Нормальное ускорение:
.
Вектор направлен к центру окружности.

Автор: Олег Одинцов . Опубликовано: 09-04-2016

Источник

iSopromat.ru

Рассмотрим определение скорости и ускорения точек при естественном способе задания движения:

— единичный вектор касательной, тогда

Алгебраическая скорость – это проекция вектора скорости на касательную, равная производной от дуговой координаты по времени.

Если производная положительна, то точка движется в положительном направлении отсчета дуговой координаты.

поскольку τ — переменный по направлению вектор, то:

определяется только свойствами траектории в окрестности данной точки, при этом

n — единичный вектор главной нормали,
ρ — радиус кривизны траектории в данной точке.

т.е. вектор ускорения раскладывается на две составляющие — касательное и нормальное ускорения:

алгебраическое значение касательного ускорения (проекция вектора ускорения на касательную) характеризует изменение скорости по величине;

Движение точки ускоренное, если знаки проекций векторов скорости и ускорения на касательную совпадают.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

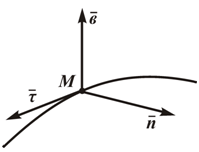
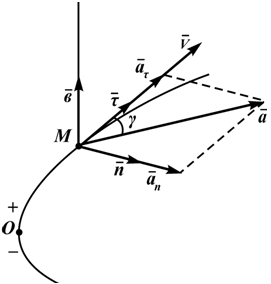
При естественном способе задания движения точки предполагается определение параметров движения точки в подвижной системе отсчета, начало которой совпадает с движущейся точкой, а осями служат касательная, нормаль и бинормаль к траектории движения точки в каждом ее положении.

τ — орт касательной;
n — орт нормали;
b — орт бинормали;

Единичные орты τ, n, b определяют направление соответствующих осей в каждой точке кривой.

Чтобы задать закон движения точки естественным способом необходимо:

знать траекторию движения;
установить начало отсчета на этой кривой;
установить положительное направление движения;
дать закон движения точки по этой кривой, т.е. выразить расстояние от начала отсчета до положения точки на кривой в данный момент времени ∪OM=S(t).

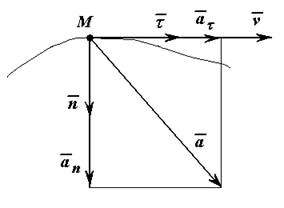
Зная эти параметры можно найти все кинематические характеристики точки в любой момент времени (рисунок 1.5).

Скорость и ускорение точки

Скорость точки при естественном способе задания её движения определяется по формулам

Первая формула определяет величину и направление вектора скорости, вторая формула только величину.

Ускорение определяется как производная от вектора скорости:

оно характеризует быстроту изменения величины скорости точки;

Нормальное ускорение точки

характеризует быстроту изменения направления вектора скорости;

ρ — радиус кривизны траектории в данной точке (например, для окружности: ρ = R, для прямой линии ρ = ∞).

Полное ускорение точки при естественном способе задания движения определяется следующим образом (рисунок 1.5):

Ранее отмечалось, что всегда можно перейти от одного способа задания закона движения точки к другому, например, от координатного к векторному. Поэтому, преобразовывая одни и те же формулы, можно получить другое их написание.

Далее, для естественнго способа задания движения точки, получаем

Источник

При естественном способе задания движения точки ее касательное ускорение определяется второй

1. Система сходящихся сил, действующих на твердое тело, имеет равнодействующую, которая равна геометрической сумме этих сил и проходит через точку пересечения их линий действия.
2. Для равновесия тела под действием системы сходящихся сил необходимо и достаточно, чтобы были равны нулю суммы моментов всех сил данной системы на каждую из координатных осей.
3. Укажите количество независимых уравнений равновесия при действии пространственной системы параллельных сил: 3.
4. Система двух равных по модулю параллельных сил, направленных в противоположные стороны, называется парой сил.

5. Реакция идеального стержня направлена вдоль стержня.
6. Вектор момента пары сил — это свободный вектор.
8. Укажите количество независимых уравнений равновесия при действии на тело плоской системы параллельных сил: 2.
9. Система сил, действующих на твердое тело, линии действия которых лежат в одной плоскости — это плоская система сил.
10. Реакция сферического шарнира может быть представлена тремя составляющими.
11. Одной из задач статики является установление условий равновесия тел при действии различных систем сил.
12. Алгебраическим моментом силы относительно центра называется взятое со знаком плюс или минус произведение модуля силы на плечо.
13. Силы, действующие на твердое тело и не являющиеся реакциями связей, называются активными.
14. Абсолютно твердое тело — тело, у которого расстояния между любыми двумя точками остается неизменным.
15. Сила, эквивалентная данной системе сил, называется равнодействующей.
16. Укажите количество независимых уравнений равновесия при действии на тело произвольной пространственной системы сил:6.
17. Тела, ограничивающие перемещение данного тела, называются связями.
18. Для равновесия твердого тела, находящегося под действием плоской системы сил, необходимо и достаточно, чтобы суммы проекций сил на две координатные оси и сумма моментов сил относительно произвольной точки равнялись нулю.
19. Две системы сил эквивалентны между собой, если, не нарушая состояния тела, одну систему сил можно заменить другой.
20. Плечо силы — это расстояние от центра момента до линии действия силы.
21. Момент пары сил равен моменту одной из сил пары относительно точки приложения другой силы.

22. Алгебраический момент пары сил равен алгебраическому моменту одной из сил пары относительно точки приложения другой силы или, то же самое, равен взятому со знаком плюс или минус произведению модуля одной из сил пары на плечо.
23. Силы, с которыми связи действуют на данное тело, называются реакциями связей.
24. Укажите количество независимых уравнений равновесия при действии на тело произвольной плоской системы сил: 3.
25. Реакция опорной точки перпендикулярна опирающейся поверхности.
26. Теорема о трех силах: Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.
27. Две пары, действующие на твердое тело и лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен геометрической сумме моментов составляющих пар.
28. Реакция идеальной нити направлена по нити от закрепленного тела.
29. Сумма моментов сил пары относительно произвольной точки равна моменту пары.
30. Для равновесия твердого тела под действием системы сходящихся сил, необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут.
31. Задачей статики является изучение методов преобразования систем сил в другие эквивалентные данным.
32. Реакция жесткой заделки состоит из одной силы и пары сил. Момент этой пары называется моментом заделки.
33. Моментом силы относительно оси называется алгебраическая величина, равная проекции вектора момента силы относительно произвольной точки оси на эту ось.
34. Реакция цилиндрического шарнира лежит в плоскости, перпендикулярной оси шарнира, может быть представлена двумя взаимно-перпендикулярными составляющими.

35. Для равновесия твердого тела под действием произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор системы сил и главный момент системы сил относительно произвольно выбранного центра равнялись нулевым векторам.
36. Укажите количество независимых уравнений равновесия при действии на тело пространственной системы сходящихся сил: 3.
37. Для характеристики вращательного действия силы вводится понятие момента силы относительно центра (или точки).
38. Задача статики о равновесии системы тел называется статически определенной, если число неизвестных не превышает числа уравнений равновесия.
39. Моментом силы относительно центра называется векторное произведение радиус-вектора, проведенного из данного центра в точку приложения силы, на вектор силы.
40. Существуют ли эквивалентные формы записи уравнений равновесия твердого тела под действием плоской системы сил?
Да
41. Пару сил, приложенную к твердому телу, можно перемещать в плоскости действия, сохраняя при этом ее момент.
42. Система сил, линии действия которых пересекаются в одной точке, называется сходящейся.
43. Для равновесия системы пар, действующих на твердое тело, необходимо и достаточно, чтобы сумма моментов пар равнялась нулю.
44. Пару сил, действующую на твердое тело, можно переносить в любую плоскость, параллельную плоскости ее действия.
45. Аксиомы статики — это простейшие правила эквивалентного преобразования систем сил, простейшие условия равновесия и взаимодействия тел.
46. Для равновесия твердого тела под действием пространственной системы параллельных сил необходимо и достаточно, чтобы сумма проекций всех сил на координатную ось, параллельную силам, и суммы моментов всех сил относительно остальных осей были равны нулю.
47. Теоремы о парах это простейшие правила эквивалетного преобразования пар и их систем.
48. Реакция гладкой поверхности направлена по нормали к этой поверхности.
49. Не изменяя действия силы на твердое тело, ее можно переносить параллельно самой себе в любую точку тела, добавляя при этом пару сил, момент которой равен моменту данной силы относительно новой точки приложения.
50. Расстояние между линиями действия сил пары — это плечо пары сил.
51. Коэффициент пропорциональности в зависимости максимального момента сопротивления качению от нормальной реакции – это коэффициент трения качения.
52. Поверхность, образованная линией действия максимальной реакции при стремлении сдвинуть тело в различных направлениях, — это конус трения.
53. Задачей расчета ферм является определение реакций внешних связей и усилий в стержнях.
54. На практике используются различные способы нахождения центра тяжести. Один из основных — это
экспериментальный метод (при подвешивании тела за любую точку его центр тяжести лежит на линии подвеса).
55. При определении усилий в стержнях фермы полагают, что стержни растнуты, направляя силы реакций от узлов. Отрицательный знак усилия, полученный в результате решения, означает, что соответствующий стержень сжат.
56. У статически определимых ферм число стержней s и число узлов n связаны соотношением: s=2n-3.
57. При повороте всех сил системы параллельных сил на один и тот же угол линия действия равнодействующей повернется в ту же сторону на тот же угол вокруг некоторой точки. Эта точка называется центром параллельных сил.
58. Ферма — это жесткая (геометрически неизменяемая) стержневая конструкция. Точка соединения стержней — узел.
59. Основными методами расчета усилий в стержнях плоских ферм являются: метод вырезания узлов и метод сечений (Риттера).
60. В результате экспериментальных исследований были установлены законы Амонтона − Кулона:
2) Максимальное значение силы трения скольжения не зависит от площади контакта, а определяется величиной нормальной реакции, материалом и состоянием контактирующих поверхностей.

61.Количество независимых уравнений равновесия при действии на ферму произвольной плоской системы сил.
3

62.Центром тяжести твердого тела называется центр параллельных сил тяжести частиц данного тела.
63. Количество независимых уравнений равновесия узла фермы, находящегося под действием плоской системы сходящихся сил:
2

64. Сопротивление, возникающее при качении одного тела по поверхности другого, — это трение качения.
65. На практике используются различные способы нахождения центра тяжести. Один из основных — это аналитический метод (интегрирование по областям, заданным аналитическими выражениями).
66. На практике используются различные способы нахождения центра тяжести. Один из основных — это метод разбиения на части (для составных тел).
67. 1) Mmaxc=Nδ – Закон трения качения

2)Fmaxтр=fN – Закон трения скольжения

68. Коэффициент трения скольжения — коэффициент пропорциональности в зависимости максимальной силы трения от нормальной реакции при неизменном состоянии контактирующих поверхностей.
69. В результате экспериментальных исследований были установлены законы Амонтона − Кулона:
1) Сила трения скольжения при равновесии тела меняется от нуля до некоторого максимального значения.

70. Центр тяжести треугольника совпадает с точкой пересечения его медиан.

71. При стремлении сдвинуть тело, лежащее на шероховатой поверхности, возникает сила реакции, которая имеет две составляющие – нормальную и силу трения скольжения.
72. На практике используются различные способы нахождения центра тяжести. Один из основных — это метод симметрии (с учетом особенностей формы тела).
73. Одной из основных задач кинематики твердого тела является определение кинематических характеристик отдельных точек тела.
74. Кинематическая мера движения точки, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета — это скорость точки.
75. Движение твердого тела, при котором любая прямая, связанная с телом, остается параллельным своему начальному положению — это поступательное движение.
76. Скорость точки − это кинематическая мера ее движения, равная производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета.
77. Кинематическая мера движения точки, равная производной по времени от скорости этой точки в рассматриваемой системе отсчета — это ускорение точки.
78. Одной из основных задач кинематики твердого тела является описание способов задания движения твердого тела.
79. Кинематическая мера движения точки, равная второй производной по времени от радиус-вектора этой точки в рассматриваемой системе отсчета — это ускорение точки.
80. Задачей кинематики является определение кинематических характеристик движения точки (скорости, ускорения) по заданному закону движения.
81. Нормальное ускорение точки — это проекция вектора ее ускорения на главную нормаль к траектории движения.
82. Ускорение точки характеризует изменение вектора скорости по величине и направлению.
83. Изменение скорости точки по величине характеризует касательное ускорение.
84. При естественном способе задания движения задаются: траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты.
85. Вектор углового ускорения − это производная вектора угловой скорости по времени.
86. Вращательным называется движение твердого тела, имеющего две неподвижные точки. Прямая, проходящая через эти точки — это ось вращения.
87. Нормальное ускорение точки определяется отношением квадрата ее скорости к радиусу кривизны траектории.
88. Механическое движение − это изменение положения одного тела относительно другого (тела отсчета), с которым связана система координат.
89. Алгебраическое значение касательного ускорения точки — это проекция вектора ускорения на касательную к траектории движения точки.
90. При естественном способе задания движения точки ее касательное ускорение определяется второй производной от дуговой координаты по времени.

91. Нормальное ускорение точки характеризует изменение ее скорости по направлению.
92. При поступательном движении твердого тела траектории, скорости и ускорения точек тела одинаковы.
93. Одной из основных задач кинематики точки является описание способов задания движения точки.
94. Одной из основных задач кинематики твердого тела является определение кинематических характеристик движения твердого тела.
95. Геометрическое место последовательных положений движущейся точки в рассматриваемой системе отсчета − это траектория точки.
96. При векторном способе задания движения точки ее положение определяется радиус-вектором, проведенным из неподвижной точки, связанной с телом отсчета.
97. Алгебраическая скорость − проекция вектора скорости на касательную, равная производной от дуговой координаты по времени.
98. Кинематическая мера изменения скорости — ускорение точки.
99. Естественные оси (касательная, главная нормаль, бинормаль) − это оси подвижной прямоугольной системы координат с началом в движущейся точке. Их положение определяется траекторией движения.
100. Система координат, в которой рассматривается движение точки, и тело отсчета называются системой отсчета.
101. При координатном способе задания движения задаются координаты точки как функции времени.
102. Вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости – это вектор угловой скорости.
103. Движение точки (или тела) по отношению к подвижной системе отсчета — относительное движение.
104.
v⃗ =v⃗r+v⃗ e — теорема сложения скоростей

a⃗ =a⃗ r+a⃗ e+a⃗ c, a⃗ c=2ω⃗ e×v⃗ r – Теорема Кориолиса

104. Теорема о сложении скоростей: При сложном движении точки абсолютная скорость равна сумме ее относительной и переносной скоростей.
105. Переносное ускорение точки − это ускорение того места подвижной системы координат, с которым в данный момент совпадает движущаяся точка.
106. Угловая скорость тела при его плоском движении, скорость его произвольной точки A и расстояние от этой точки до мгновенного центра скоростей P связаны соотношением:
ω=vAAP
Да

107. Способы вычисления ускорения Кориолиса:
1. По правилу вычисления векторного произведения.
2. По правилу Жуковского.
108. Движение, при котором все точки тела движутся в плоскостях, параллельных некоторой неподвижной плоскости – это плоское (или плоско-параллельное) движение твердого тела.
109. Скорость того места подвижной системы координат, с которым в данный момент совпадает движущаяся точка — это переносная скорость.
110. Движение подвижной системы отсчета относительно основной — переносное движение.
112. Движение плоской фигуры можно рассматривать как сложное, которое складывается из относительного и переносного. Поступательное движение подвижной системы координат вместе с произвольной точкой, жестко связанной с фигурой, называемой полюсом – это переносное движение.
113. Зависит ли закон изменения угла от выбора полюса?
Не зависит

114. Зависит ли угловая скорость твердого тела, совершающего плоское движение, от выбора полюса?

Не зависти
115. Правило Жуковского: Для определения направления ускорения Кориолиса надо вектор относительной скорости спроецировать на плоскость, перпендикулярную оси вращения в переносном движении, и повернуть в сторону вращения на угол 90 град.
116. Модуль ускорения Кориолиса:
ac=2∣ω⃗ e∣∣v⃗ r∣sinα
Верно

117. Скорость любой точки плоской фигуры находится как скорость во вращательном движении вокруг мгновенного центра скоростей.
118. Абсолютное ускорение точки − это ускорение точки в основной системе отсчета.
119. Движение точки (или тела) по отношению к основной системе отсчета — абсолютное движение.

120. Эти уравнения определяют движение плоской фигуры:
xA=xA(t),
yA=yA(t),
φ=φ(t)
Да

121. Теорема Кориолиса: При непоступательном переносном движении абсолютное ускорение точки находится как сумма трех ускорений: относительного, переносного и ускорения Кориолиса.
122. Движение плоской фигуры можно рассматривать как сложное, которое складывается из относительного и переносного. Вращение плоской фигуры вокруг выбранного полюса — это плоское движение.
123. Абсолютная скорость точки − это скорость точки в основной системе отсчета.
124. Относительное ускорение точки — это ускорение точки в подвижной системе отсчета.
125. Движение точки (или тела), которое рассматривается одновременно в разных системах отсчета, — это сложное движение.
126. Теорема. Скорость любой точки тела при плоском движении находится как сумма скорости полюса и скорости данной точки во вращательном движении вокруг полюса.
127.
v⃗ ,a⃗ — Кинематические характеристики абсолютного движения
v⃗ e,a⃗ e — Кинематические характеристики переносного движения
v⃗ r,a⃗ r — Кинематические характеристики относительного движения

128. При задании плоского движения за полюс может приниматься любая точка тела.
129. Относительная скорость точки — это скорость точки в подвижной системе отсчета.
130. Ускорение Кориолиса учитывает изменение относительной скорости, вызванное переносным движением, и изменение переносной скорости, вызванное относительным движением.
131. Теорема. При непоступательном движении плоской фигуры существует жестко связанная с ней точка, скорость которой в данный момент движения равна нулю. Эта точка является мгновенным центром скоростей.

Источник