При анализе вещества двумя способами по двум независимым выборкам объемов

Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. №567, стр.214

По двум независимым выборкам, объемы которых n=40 и m=50, извлеченным из нормальных генеральных совокупностей, найдены выборочные средние соответственно равные 130 и 140. Генеральные дисперсии известны: D(X)=80, D(Y)=100. Требуется при уровне значимости 0,01 проверить нулевую гипотезу Н₀:М(X)=М(Y) при конкурирующей гипотезе H₁:M(X)≠M(Y).

Другие задачи по теории вероятности

По выборке объема n=30 найден средний вес 130г изделий, изготовленных на первом станке; по выборке объема m=40 найден средний вес 125г изделий, изготовленных на втором станке. Генеральные дисперсии известны: D(X)=60гa 2 , D(Y)=80га 2 . Требуется, при уровне значимости 0,05, проверить нулевую гипотезу H₀: М(X)=М(Y) при конкурирующей гипотезе М(X)≠М(Y). Предполагается, что случайные величины X и Y распределены нормально и выборки независимы.

По выборке объема n=50 найден средний размер 20,1мм диаметра валиков, изготовленных автоматом №1; по выборке объема m=50 найден средний размер 19,8мм диаметра валиков, изготовленных автоматом №2. Генеральные дисперсии известны: D(X)=1,75мм 2 , D(Y)=1,375мм 2 . Требуется, при уровне значимости 0,05, проверить нулевую гипотезу H₀:М(X)=М(Y) при конкурирующей гипотезе М(X)≠М(Y). Предполагается, что случайные величины X и Y распределены нормально и выборки независимы.

По двум независимым малым выборкам, объемы которых n=12 и m=18, извлеченным из нормальных генеральных совокупностей X и Y, найдены выборочные средние: 31,2, 29,2 и исправленные дисперсии: s_X 2 =0,84 и s_Y 2 =0,40. Требуется при уровне значимости 0,05 проверить нулевую гипотезу H₀:М(X)=М(Y) при конкурирующей гипотезе Н₁:M(Х)≠М(Y).

Источник

Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. №556, стр.208

По двум независимым выборкам, объемы которых n₁=14 и n₂=10, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии s_X 2 =0,84 и s_Y 2 =2,52. При уровне значимости α=0,1, проверить нулевую гипотезу H₀:D(X)=D(Y) о равенстве генеральных дисперсий, при конкурирующей гипотезе H₁:D(X)≠D(Y).

Другие задачи по теории вероятности

По двум независимым выборкам, объемы которых n₁=9 и n₂=6, извлеченным из нормальных генеральных совокупностей X и Y, найдены выборочные дисперсии D_В(X)=14,4 и D_В(Y)=20,5. При уровне значимости α=0,1, проверить нулевую гипотезу H₀:D(X)=D(Y) о равенстве генеральных дисперсий, при конкурирующей гипотезе H₁:D(X)≠D(Y).

Двумя методами проведены измерения одной и той же физической величины.

Получены следующие результаты:

Можно ли считать, что оба метода обеспечивают одинаковую точность измерений, если принять уровень значимости α=0,1? Предполагается, что результаты измерений распределены нормально и выборки независимы.

Для сравнения точности двух станков-автоматов взяты две пробы (выборки), объемы которых n₁=10 и n₂=8. В результате измерения контролируемого размера отобранных изделий получены следующие результаты:

Можно ли считать, что станки обладают одинаковой точностью [H₀:D(X)=D(Y)], если принять уровень значимости α=0,1 и в качестве конкурирующей гипотезы Н₁:D(X)≠D(Y).

Из нормальной генеральной совокупности извлечена выборка объема n=21 и по ней найдена исправленная выборочная дисперсия s 2 =16,2. Требуется при уровне значимости 0,01 проверить нулевую гипотезу H₀:σ 2 =σ₀ 2 =15, приняв в качестве конкурирующей гипотезы Н₁:σ 2 >15.

Из нормальной генеральной совокупности извлечена выборка объема n=17 и по ней найдена исправленная выборочная дисперсия s 2 =0,24. Требуется при уровне значимости 0,05 проверить нулевую гипотезу H₀:σ 2 =σ₀ 2 =0,18, приняв в качестве конкурирующей гипотезы Н₁:σ 2 >0,18.

Из нормальной генеральной совокупности извлечена выборка объема n=31:

Требуется при уровне значимости 0,05 проверить нулевую гипотезу H₀:σ 2 =σ₀ 2 =0,18, приняв в качестве конкурирующей гипотезы Н₁:σ 2 >0,18.

Точность работы станка-автомата проверяется по дисперсии контролируемого размера изделий, которая не должна превышать σ₀ 2 =0,1. Взята проба из 25 случайных отобранных изделий, причем получены следующие результаты измерений:

Требуется при уровне значимости 0,05 проверить, обеспечивает ли станок требуемую точность.

Источник

Задачи с решениями

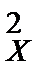
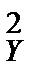
Задача 9.1. По двум независимым выборкам объемов n₁ = 10 и n₂ = 15, извлеченным из нормальных генеральных совокупностей X и Y, найдены оценки дисперсий: s = 8,42, s = 4,23. При уровне значимости α = 0,05 проверить гипотезу H₀: D(X)=D(Y) при конкурирующей гипотезе H₁: D(X)>D(Y).

Решение.1) По данным выборки вычисляем

= .

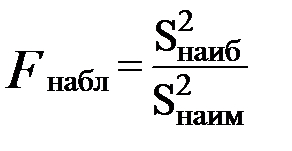
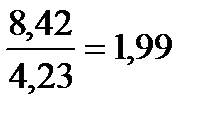
2) По табл. П 2.7 (см. приложение 2), учитывая значения

3) Сравниваем: так как 1,99

Решение. 1) По данным выборок вычисляем:

= 9 + 14 + 19 = 42,

=

=

= .

= ,

.

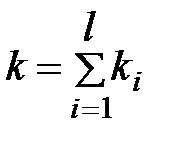
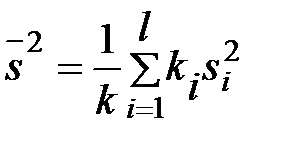
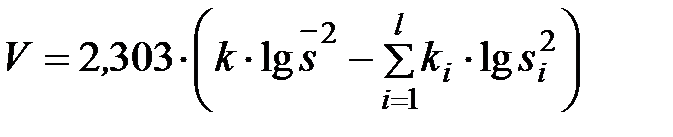
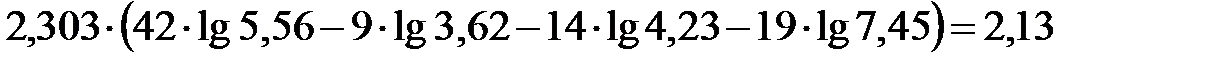
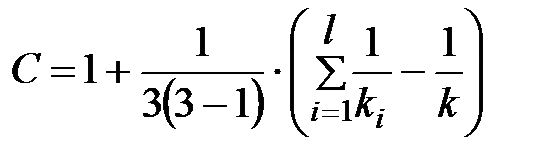
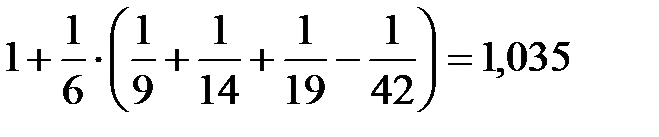
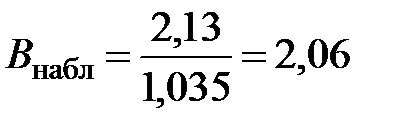
2) По табл. П 2.5 (см. приложение 2), учитывая значения

α = 0,05, k = 3 – 1 = 2,

3) Сравниваем: так как 2,06 2 _крит , следовательно нет основания отвергать нулевую гипотезу.

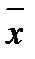
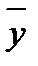
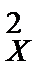
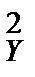
Задача 9.4. По двум независимым выборкам объемов n₁=10 и n₂=16, извлеченным из нормальных генеральных совокупностей X и Y, найдены оценки математических ожиданий =2,5, =3,1 и исправленные выборочные дисперсии s =0,62, s =0,43 . Проверить нулевую гипотезу: H₀ : M(X) = M(Y) при конкурирующей гипотезе H₁ : M(X) ≠ M(Y) и уровне значимости α = 0,01.

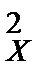
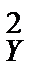
Решение. 1) Так как s ≠ s , то предварительно проверим гипотезу H₀: D(X)=D(Y) о равенстве генеральных дисперсий при конкурирующей гипотезе H₁: D(X)>D(Y). Для этого поступаем по аналогии с решением 1 задачи.

а) По данным выборки вычисляем

= ;

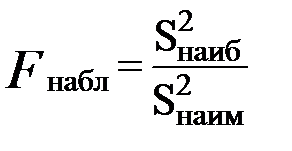
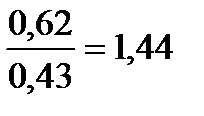
б) По табл. П 2.7 (см. приложение 2), учитывая значения

в) Сравниваем: так как 1,44

=

= =

= .

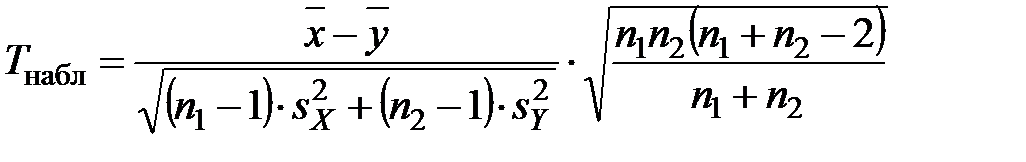
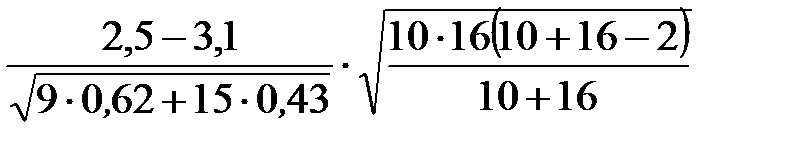
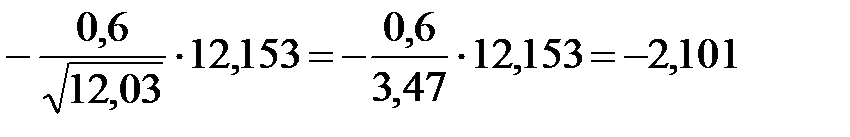
в) Сравнить числа T_крит и 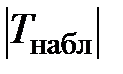: так как 2,101 1,96, т.е. N_набл > N_крит , то гипотезу H₀ отвергают. Значит, различие генеральных математических ожиданий значительное.

Задачи

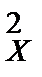
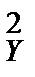
9.1. По двум независимым выборкам объемов n₁ = 10 и n₂ = 13, извлеченным из нормальных генеральных совокупностей X и Y , найдены исправленные выборочные дисперсии s = 0,52 и s = 0,28. При уровне значимости α = 0,01 проверить гипотезу H₀: D(X) = D(Y) при конкурирующей гипотезе H₁: D(X) > D(Y).

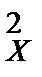
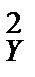
9.2. По двум независимым выборкам объемов n₁ = 15 и n₂ = 10, извлеченным из нормальных генеральных совокупностей X и Y , найдены исправленные выборочные дисперсии s = 1,92 и s = 3,21. При уровне значимости α = 0,1 проверить гипотезу H₀ : D(X) = D(Y) при конкурирующей гипотезе H₁: D(X) ≠ D(Y).

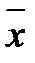
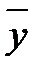
9.3. По двум независимым выборкам объемов n₁ = 15 и n₂ = 10, извлеченным из нормальных генеральных совокупностей X и Y c дисперсиями D(X) = 25, D(Y) = 32, найдены выборочные средние =53, = 61. При уровне значимости α = 0,1 проверить нулевую гипотезу H₀ : M(X)=M(Y) при конкурирующей гипотезе H₁ : M(X) ≠ M(Y).

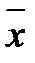
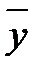
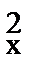
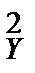
9.4. По двум независимым выборкам объемов n₁ = 15 и n₂ = 12, извлеченным из нормальных генеральных совокупностей X и Y найдены выборочные средние =11,2, = 15,7 и исправленные выборочные дисперсии s = 0,58 , s = 0, 83. При уровне значимости α = 0,05 проверить нулевую гипотезу H₀ : M(X)=M(Y) при конкурирующей гипотезе H₁: M(X) ≠ M(Y).

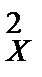
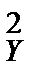
9.6. По двум независимым выборкам объемов n₁=12 и n₂=18, извлеченным из нормальных генеральных совокупностей X и Y найдены исправленные выборочные дисперсии s = 25,31 , s = 10,23. При уровне значимости α = 0,05 проверить гипотезу H₀: D(X) = D(Y) при конкурирующей гипотезе H₁ : D(X) > D(Y).

9.7. По двум независимым выборкам объемов n₁ = 12 и n₂ = 10, извлеченным из нормальных генеральных совокупностей X и Y найдены исправленные выборочные дисперсии D_в(X) = 12,3, D_в(Y) = 18,5. При уровне значимости α = 0,02 проверить гипотезу H₀: D(X) = D(Y) при конкурирующей гипотезе H₁ : D(X) ≠ D(Y).

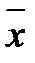
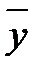
9.8. По двум независимым выборкам объемов n₁ = 40 и n₂ = 30, извлеченным из нормальных генеральных совокупностей X и Y c дисперсиями D(X) = 80, D(Y) = 70, найдены выборочные средние = 120, = 115. При уровне значимости α = 0,01 проверить нулевую гипотезу H₀ : M(X) = M(Y) при конкурирующей гипотезе H₁: M(X) ≠ M(Y).

9.9. Из двух партий изделий, изготовленных на двух одинаково настроенных станках, извлечены две выборки:

xi	2,2	2,6	2,8	3,1
mi

yi	2,5	2,7	2,8	3,0
mi

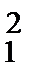
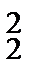
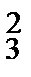
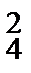
9.10. По четырем независимым выборкам объемов n₁ = 12 и n₂ = 15, n₃ = 18 и n₄ = 20 извлеченным из нормальных генеральных совокупностей X, Y, Z и U, найдены исправленные выборочные дисперсии S = 0,27 , S = 0,52, S = 0,85 и S = 0,99. При уровне значимости α = 0,01 проверить гипотезу H₀: D(X) = D(Y) = D(Z) = D(U).

Ответы

Указание. Предварительно проверить равенство дисперсий при заданном уровне значимости

9.5. H₀ принимается: B_набл = 4,064 , χ 2 _крит = 6,0.

Указание: Предварительно проверить равенство дисперсий при заданном уровне значимости

9.10. H₀ принимается: B_набл. = 2,918 , χ 2 = 11,3.

Источник