Презентация с алгебраическим способом задачи

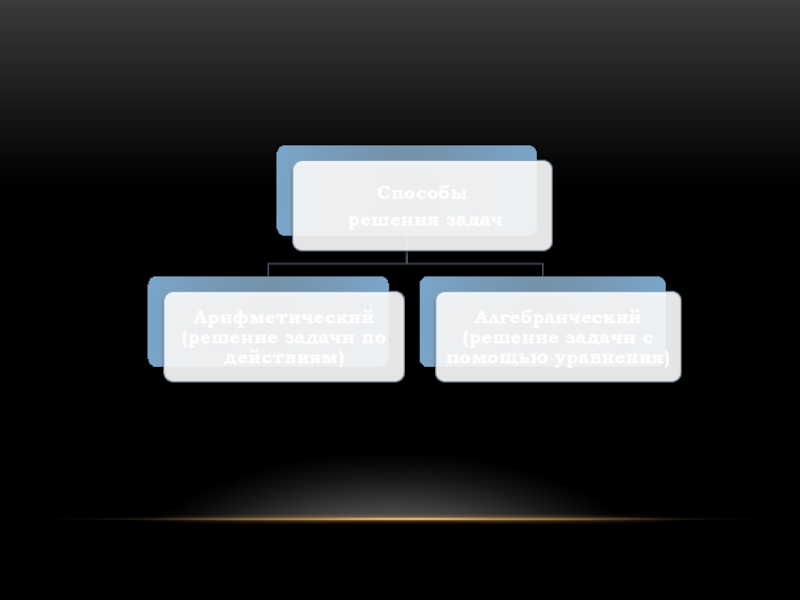
презентация к уроку алгебры 7 класс «Алгебраический способ решения задач»
презентация к уроку по алгебре (7 класс) на тему

Первый урок по алгебре в 7 классе «Алгебраический способ решения задач» к учебнику Дорофеева Г.В.

Скачать:

Вложение	Размер
algebraicheskiy_sposob_resheniya_zadach.pptx	411.1 КБ

Предварительный просмотр:

Подписи к слайдам:

“Математическая задача иногда столь же увлекательна, как кроссворд, и напряженная умственная работа может быть столь же желанным упражнением, как стремительный теннис” “Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия” Д. Пойа

18.11.2016 7 класс Алгебраический способ решения задач

Цель урока выработать навыки решения текстовых задач разными способами

Разминка Вариант 1 v t s Вариант 2 v t s 24 км/ч, 150 с, 0,1 мин, 194 ч, 0,009 м, 594 м/с, 709 км. 24 мин, 55 км/ч, 210км, 120 м/мин, 0, 12 м, 13 с, 132 м/с

Разминка Вариант 1 v t s 59 км/ч 0,01 ч 10 с 18,4 км 0,1 км/ч 73 км Вариант 2 v t s 120 мин 124,8 км 12 км/ч 0,3 ч 1,6 км/ч 96 км

Разминка Вариант 1 Для класса купили х тетрадей по 2 руб. за тетрадь и у тетрадей по 3 руб. за тетрадь. Сколько рублей заплатили за покупку? Поезд шел до остановки a ч со скоростью v км/ч, а затем после остановки b ч с той же скоростью. Какое расстояние прошел поезд? Вариант 2 От куска материи длиной с (м) три раза отрезали по а (м). Сколько метров материи осталось в куске? В семье c детей. Мама принесла a яблок и разделила их поровну между детьми. Затем пришел папа и принес b яблок. Он их тоже разделил между детьми поровну. Сколько яблок получил каждый из детей?

Проверка v t s v t s 24 км/ч, 150 с, 0,1 мин, 194 ч, 0,009 м, 594 м/с, 709 км. 24 км/ч 150 с 0,009 м 594 м/с 0,1 мин 709 км 194 ч 55 км/ч 24 мин 13 с 120 м/мин 210 км 0,12 м 132 м/с 24 мин, 55 км/ч, 210км, 120 м/мин, 0, 12 м, 13 с, 132 м/с

1 вариант v t s 59 км/ч 0,01 ч 10 с 18,4 км 0,1 км/ч 73 км 0, 59 км 1, 84 км/с 730 ч

2 вариант v t s 120 мин 124, 8 км 12 км/ч 0,3 ч 1,6 км/ч 96 км 62,4 60 ч 3,6 км

Разминка Вариант 1 Для класса купили х тетрадей по 2 руб. за тетрадь и у тетрадей по 3 руб. за тетрадь. Сколько рублей заплатили за покупку? 2х + 3у Вариант2 От куска материи длиной с (м) три раза отрезали по а (м). Сколько метров материи осталось в куске? с – 3а

Разминка Вариант 1 Поезд шел до остановки a ч со скоростью v км/ч, а затем после остановки b ч с той же скоростью. Какое расстояние прошел поезд? va + vb Вариант 2 В семье c детей. Мама принесла a яблок и разделила их поровну между детьми. Затем пришел папа и принес b яблок. Он их тоже разделил между детьми поровну. Сколько яблок получил каждый из детей?

Решить задачу арифметическим способом В семье две пары близнецов, родившихся с разницей в три года. В 2012 году всем вместе исполнилось 50 лет. Сколько лет было каждому из близнецов в 2010 году?

Арифметический способ 1) Сколько лет двум парам близнецов в 2010 году, если бы им было лет поровну? 50 – 2 – 2 – 5 – 5 = 36 (лет) 2) По сколько лет младшим близнецам? 36 : 4 = 9 (лет) 3) По сколько лет старшим близнецам? 9 + 3 = 12 (лет) Ответ: по 9 и 12 лет

Работа с текстом учебника пункт 4.1., страница103 а) С чего начинается решение задачи алгебраическим способом; б) Как называется равенство, содержащее букву; в) Как и когда зародился алгебраический способ решения задач.

Алгебраический способ 2010 год 2012 год Младшие близнецы Старшие близнецы х х + 3 х + 2 х + 5 50 лет ( х +2) + ( х + 2) + ( х + 5) + ( х + 5) = 50

Решение задач в парах На трех полках 50 книг. На средней полке на 4 книги меньше, чем на верхней, и на 2 книги больше, чем на нижней полке. Сколько книг на каждой полке? Составьте 3 уравнения, обозначив последовательно буквой х число книг на каждой из полок. Какое уравнение легче было составить?

Ответы 1 вариант: х + (х – 4) + (х – 6) = 50 2 вариант: (х + 4) + х + (х – 2) = 50 3 вариант: (х + 6) + (х + 2) + х = 50

Составление уравнений в группах 1 группа На одной овощебазе 500 т картофеля, а на другой 700 т. Ежедневно с первой базы отправляют в овощные магазины 20 ц картофеля, а со второй – 30 ц. Через сколько дней картофеля на овощных базах окажется поровну? 2 группа Сплав меди и цинка содержал 82% меди. После добавления в сплав 18 кг цинка процентное содержание меди в сплаве понизилось до 70%. Сколько меди и сколько цинка было в сплаве изначально?

Составление уравнений в группах 3 группа В одной машине 3 т яблок, а в другой – 5 т яблок. Из первой машины выгрузили несколько ящиков по 15 кг в каждом, а из второй – в 2 раза больше ящиков по 20 кг в каждом. После этого в первой машине осталось столько же яблок, сколько во второй. Сколько ящиков выгрузили из каждой машины? 4 группа. В клетке находятся фазаны и кролики. Известно, что у них 35 голов и 94 ноги. Узнайте число кроликов и число фазанов?

Жизнь Диофанта По преданию, на могильном камне имелась такая надпись: “Путник! Под этим камнем покоится прах Диофанта, умершего в глубокой старости. Шестую часть своей долгой жизни он был ребёнком, двенадцатую – юношей, седьмую провел неженатым. Через пять лет после женитьбы у него родился сын, который прожил вдвое меньше отца. Через четыре года после смерти сына уснул вечным сном и сам Диофант, оплакиваемый своими близкими. Скажи, если умеешь считать, сколько лет прожил Диофант?”

Способ подбора Число лет Диофанта делится на 6, 12, 7 и 2; НОК (6; 12; 7; 2) = НОК(12; 7) = 84. Заметим, что большие значения нереальны. Ответ: 84 года.

Алгебраический способ Пусть Диофант прожил х лет. Тогда составим и решим уравнение: 14х+7х+12х+420+42х+336=84х 9х=756 х=84

Примеры исторических задач Школа Пифагора Древнегреческая задача о статуи Минервы Задача великого французского математика XVIII века Э. Безу

Итог урока Задача Трудная, непонятная. Думать, рассуждать, решать. Развивает логическое мышление. Получится!

Домашнее задание Прочитать пункт 4.1, №№ 337, 343(б). Подобрать интересные задачи

Спасибо за урок

По теме: методические разработки, презентации и конспекты

Конспект урока алгебры по теме: «Решение задач с помощью уравнений».

Цель: — используя игровые формы, проверить умения и навыки учащихся при составлении квадратных и рациональных уравнений для практических задач; — с помощью экспресс — тестирования выяснить характ.

Урок алгебры 7 класс. Решение задач с помощью уравнений

Презентация к уроку алгебры по теме: «Решение задач с помощью уравнений».

Урок-конференция (заключительный) по данной теме.

Презентация к уроку алгебры «Графический способ решения уравнений»

Данный ЦОР может быть использован при изучении темы «Графическое решение уравнений» в 9 классе.

Методическая разработка урока алгебры по теме «Решение задач с помощью систем уравнений»

Урок алгебры в 7 классе по теме «Решение задач с помощью систем уравнений».

Презентация к уроку алгебры «Арифметическая прогрессия. Решение задач»

Презентация к уроку алгебры в 9 классе УМК Алимов и др. (Колягин и др.) «Арифметическая прогрессия. Решение задач»Презентация содержит 6 задач.

Презентация к уроку алгебры по теме « Решение задач на концентрацию, смеси и сплавы».

Данная презентация представляет собой учебное пособие по решению задач данного типа. Приём решения, рассказанный в слайдах данной презентации, могут использовать как обучающиеся, так и педагоги.

Источник

Презентация на тему Решение задач алгебраическим способом

Презентация на тему Презентация на тему Решение задач алгебраическим способом из раздела Математика. Доклад-презентацию можно скачать по ссылке внизу страницы. Эта презентация для класса содержит 13 слайдов. Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!

Слайды и текст этой презентации

Автор работы: Белякова Ольга Владимировна,
учитель математики МОУ «ЛСОШ №2»
г. Лихославль Тверской области

Решение задач алгебраическим способом (с помощью уравнений) По учебнику И.И. Зубаревой, А.Г. Мордковича

Цели: — показать правило решения задач алгебраическим способом; — формировать умение решать задачи арифметическим и алгебраическим способами.

Прочитайте задачу.
Постарайтесь найти разные способы решения.

В двух коробках 16 кг печенья. Найдите массу печенья в каждой коробке, если в одной из них печенья на 4 кг больше, чем в другой.

1 способ решения
(смотреть)

3 способ решения
(смотреть)

2 способ решения
(смотреть)

4 способ решения
(смотреть)

1 способ (арифметический)

16 – 4 = 12 (кг) – печенья останется в двух коробках, если из первой коробки достать 4 кг печенья.

12 : 2 = 6 (кг) – печенья было во второй коробке.

6 + 4 = 10 (кг) – печенья было в первой коробке.

Ответ: масса печенья в первой коробке – 10 кг, а во второй 6 кг.

В решении использован способ уравнивания.
Вопрос: почему он получил такое название?

2 способ (арифметический)

16 + 4 = 20 (кг) – печенья станет в двух коробках, если во вторую коробку добавить 4 кг печенья.

20 : 2 = 10 (кг) – печенья было в первой коробке.

10 — 4 = 6 (кг) – печенья было во второй коробке.

Ответ: масса печенья в первой коробке – 10 кг, а во второй 6 кг.

В решении использован способ уравнивания.

3 способ (алгебраический)

Обозначим массу печенья во второй коробке буквой х кг. Тогда масса печенья в первой коробке будет равна (х+4) кг, а масса печенья в двух коробках – ((х+4)+х) кг.
По условию задачи, в двух коробках было 16 кг печенья. Получаем уравнение:
(х+4)+х=16
х+4+х=16
2х+4=16
2х=16-4
2х=12
х=12:2
х=6
Во второй коробке было 6 кг печенья.
6+4=10 (кг) – печенья было в первой коробке.

В решении использован алгебраический способ.
Задание: Объясните, в чем отличие арифметического способа от алгебраического?

4 способ (алгебраический)

Обозначим массу печенья в первой коробке буквой х кг. Тогда масса печенья во второй коробке будет равна (х-4) кг, а масса печенья в двух коробках – (х+(х-4)) кг.
По условию задачи, в двух коробках было 16 кг печенья. Получаем уравнение:
х+(х-4)=16
х+х-4=16
2х-4=16
2х=16+4
2х=20
х=20:2
х=10
В первой коробке было 10 кг печенья.
10-4=6 (кг) – печенья было во второй коробке.

В решении использован алгебраический способ.

Какие два способа решения задачи были использованы?
Что собой представляет способ уравнивания?
Чем первый способ уравнивания отличается от второго?
В одном кармане на 10 рублей больше, чем в другом. Как можно уравнять количество денег в обоих карманах?
В чем заключается алгебраический способ решения задачи?
Чем отличается 3 способ решения задачи от 4-го?
В одном кармане на 10 рублей больше, чем в другом. Известно, что меньшее количество денег обозначили переменной х. Как будет выражаться через х количество денег в другом кармане?
Если за х обозначить большее количество денег в кармане, тогда как будет выражаться через х количество денег в другом кармане?
В магазине шампунь стоит на 25 руб дороже, чем в супермаркете. Обозначьте одну переменную буквой у и выразите другую стоимость через эту переменную.

Решите задачу арифметическим и алгебраическим способами.

С трех участков земли собрали 156 ц картофеля. С первого и второго участков картофеля собрали поровну, а с третьего – на 12 ц больше, чем с каждого из двух первых. Сколько картофеля собрали с каждого участка.

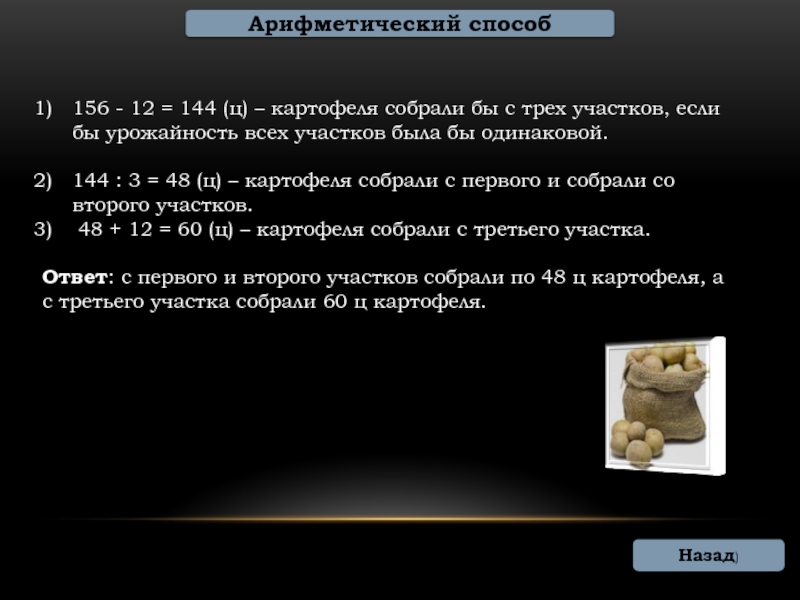
156 — 12 = 144 (ц) – картофеля собрали бы с трех участков, если бы урожайность всех участков была бы одинаковой.

144 : 3 = 48 (ц) – картофеля собрали с первого и собрали со второго участков.
48 + 12 = 60 (ц) – картофеля собрали с третьего участка.

Ответ: с первого и второго участков собрали по 48 ц картофеля, а с третьего участка собрали 60 ц картофеля.

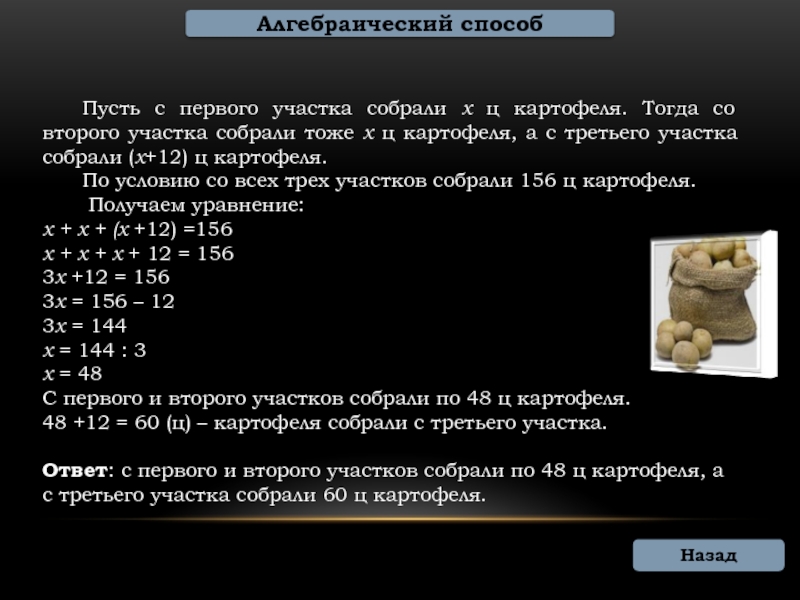
Пусть с первого участка собрали х ц картофеля. Тогда со второго участка собрали тоже х ц картофеля, а с третьего участка собрали (х+12) ц картофеля.
По условию со всех трех участков собрали 156 ц картофеля.
Получаем уравнение:
х + х + (х +12) =156
х + х + х + 12 = 156
3х +12 = 156
3х = 156 – 12
3х = 144
х = 144 : 3
х = 48
С первого и второго участков собрали по 48 ц картофеля.
48 +12 = 60 (ц) – картофеля собрали с третьего участка.

Ответ: с первого и второго участков собрали по 48 ц картофеля, а с третьего участка собрали 60 ц картофеля.

Источник