Преобразования плоскости симметрия геометрических фигур способы построения симметричных изображений

Геометрические преобразования пространства»

Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно точки , называется центральной симметрией пространства относительно точки . При этом точка отображается на себя и называется центром симметрии.

Примерами центральной симметрии являются: автомобильное колесо, окружность, куб, шар, снежинка, цветок и тд.

Симметрия относительно плоскости (зеркальная симметрия):

Определение.Преобразование пространства, при котором сохраняются расстояния между любыми двумя точками, называется движением пространства.

Свойства: при движении в пространстве прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, плоскости – в плоскости; сохраняются углы между полупрямыми.

Определение. Преобразование пространства, при котором каждая точка пространства отображается на точку, симметричную ей относительно плоскости , называется симметрией пространства относительно плоскости . Плоскость называется плоскостью симметрии.

Примеры симметрии относительно плоскости:

Определение. Параллельным переносом на вектор называется такое преобразование пространства, при котором любая точка отображается на такую точку , что выполняется векторное равенство . Это перенос (движение) всех точек пространства в одном и том же направлении, на одно и то же расстояние

Примеры параллельного переноса:

Определение. Осевая симметрия — это симметрия относительно проведённой прямой (оси).

Определение.Преобразования фигуры в фигуру называется преобразования подобия, если при этом преобразовании расстояние между точками изменяется в одно и тоже число раз. То есть преобразование, которое сохраняет форму фигуры, но изменяет их размеры.

Определение. Гомотетия — это преобразование подобия. Это преобразование, в котором получаются подобные фигуры (фигуры, у которых соответствующие углы равны и стороны пропорциональны).

Чтобы гомотетия была определена, должен быть задан центр гомотетии и коэффициент. Это можно записать: гомотетия .

Можно ли взаимно-однозначно отобразить: а) поверхность куба на поверхность другого куба; б) поверхность куба на сферу; Сделайте соответствующие рисунки.

Решение.а) Достаточно кубы расположить так, чтобы совпали их центры, а грани одного были параллельны граням другого. Тогда поверхность одного куба взаимно-однозначно отображается на поверхность другого куба посредством центрального проектирования из их общего центра. (Аналогичная задача планиметрии — о взаимно-однозначном отображении одного квадрата на другой посредством центрального проектирования.)

б) Достаточно центр сферы совместить с центром куба, тогда поверхность куба взаимно-однозначно отображается на сферу посредством центрального проектирования из их общего центра. (Аналогичная задача планиметрии — о взаимно-однозначном отображении квадрата — замкнутой ломаной — на окружность посредством центрального проектирования.)

Источник

Симметрия на плоскости
презентация к уроку по геометрии (9 класс) на тему

Урок подготовлен и проведён в 9 классе 2 отделения для слабослышащих учащихся.Целью этого урока было ознакомление учащихся с понятием симметрии, с её видами , практическим применением в геометрии и в жизни.

Скачать:

Вложение	Размер
simmetriya.ppt	860 КБ

Предварительный просмотр:

Подписи к слайдам:

Урок геометрии в 9 классе Учитель : Лежнина Е.А. Симметрия на плоскости

Изучение нового материала В геометрии существует два вида симметрии ОСЕВАЯ ЦЕНТРАЛЬНАЯ симметрия симметрия

Осевая симметрия для точки Две точки А и А 1 называются симметричными относительно прямой а , если эта прямая проходит через середину отрезка АА 1 и перпендикулярна к нему. Каждая точка прямой а считается симметричной самой себе.

Задание 1 Построить точку симметричную данной относительно прямой а

Осевая симметрия фигуры Фигура называется симметричной относительно прямой а , если для каждой точки симметричная ей точка относительно прямой а также принадлежит этой фигуре. Прямая а называется осью симметрии .

Задание 2 Определить количество осей симметрии у фигуры.

Осевая симметрия двух фигур Осевая симметрия двух фигур — это преобразование, при котором каждая точка одной фигуры переходит в симметричную точку другой фигуры относительно данной прямой.

Задание 3 Построить фигуру симметричную данной относительно прямой а

Осевая симметрия в природе, технике и архитектуре. «. быть прекрасным значит быть симметричным» Платон

Повторяющиеся фрагменты рисунка состоят из двух одинаковых частей и каждую из них можно получить из другой части поворотом на 180 градусов относительно некоторой точки.

Центральная симметрия Две точки А и А 1 называются симметричными относительно точки О , если эта точка – середина отрезка АА 1. Точка О считается симметричной самой себе. Фигура называется симметричной относительно точки О , если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии.

Центральная симметрия двух фигур. Центральная симметрия – это преобразование, при котором каждая точка фигуры переходит в симметричную относительно данной точки О.

Задание 1. Укажите центры симметрии фигур

Задание 2. Выберите фигуры, которые имеют центр симметрии и изобразите их в тетради.

Параллельный перенос Пусть а – данный вектор Параллельным переносом на вектор а называется отображение плоскости, при котором каждая точка М отображается в такую точку М1, что ММ1=а Параллельный перенос является движением

Поворот Отметим на плоскости точку О и зададим угол А Поворотом плоскости вокруг точки О на угол А называется отображение плоскости, при котором каждая точка М отображается в точку М1 так, что ОМ = ОМ1 и угол МОМ1 равен углу А Поворот является движением

По теме: методические разработки, презентации и конспекты

Третья часть блока обучающих презентаций «Координаты на плоскости»симметрия, симметрия относительно прямой, ось симметрии, симметричная фигура, координаты точек симметричных относительно осей ко.

Четвертая часть блока обучающих презентаций «Координаты на плоскости».

Учить учащихся строить точки на координатной плоскости, находить координаты точек. Выработать умение строить точки по заданным координатам, развивать воображение, наблюдательность, память. воспитывать.

1)Определение симметрии 2)Виды симметрии3)Симметрия относительно плоскости 4)Определение Центральной симметрии5)Определение Осевой симметрии6)Определение Поворотной симметрии7)Параллельный п.

2016Урок по математике в 6 классе «Координатная плоскость и симметрия&raquo.

Контрольная работа № 11 по теме «Перпендикулярные и параллельные прямые. Осевая и центральная симметрии. Координатная плоскость. Графики» для учащихся 6 класса общеобразовательной школы сост.

Контрольная работа № 11 по теме «Перпендикулярные и параллельные прямые. Осевая и центральная симметрии. Координатная плоскость. Графики» для учащихся 6 класса общеобразовательной школы сост.

Источник

Осевая и центральная симметрия

О чем эта статья:

Что такое симметрия

Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.

Ось симметрии фигуры — это прямая, которая делит фигуру на две симметричные части. Чтобы наглядно понять, что такое ось симметрии, внимательно рассмотрите рисунок.

Центр симметрии — это точка, в которой пересекаются все оси симметрии.

Вернемся к рисунку: на нем мы видим фигуры, имеющие ось и центр симметрии.

Рассмотрите фигуры с осевой и центральной симметрией.

• Ось симметрии угла — биссектриса.
• Ось симметрии равнобедренного треугольника — биссектриса, медиана, высота.
• Оси симметрии прямоугольника проходят через середины его сторон.
• У ромба две оси симметрии — прямые, содержащие его диагонали.
• У квадрата 4 оси симметрии, так как он сразу квадрат, треугольник (если его сложить пополам) и ромб.
• Ось симметрии окружности — любая прямая, проведенная через ее центр.

Витрувианский человек да Винчи — хрестоматийный пример симметрии. Принято считать, что, чем предмет симметричнее, тем он красивее. Хотя, по секрету, в природе нет ничего абсолютно симметричного, так уж задумано. Вся идеальная симметрия — дело рук человека.

Осевая симметрия

Вот как звучит определение осевой симметрии:

Осевой симметрией называется симметрия, проведенная относительно прямой. При осевой симметрии любой точке, расположенной по одну сторону прямой, всегда соответствует другая точка на второй стороне этой прямой.

При этом отрезки, соединяющие эти точки, перпендикулярны оси симметрии.

Осевая симметрия часто встречается в повседневной жизни. К сожалению, не на фото в паспорте и не в стрелках на глазах. Но её вполне себе можно встретить в половинках авокадо, на морде кота или в зданиях вокруг. Осевая симметрия — неотъемлемая часть архитектуры. Оглядитесь и поищите примеры осевой симметрии вокруг вас.

В геометрии есть фигуры, обладающие осевой симметрией: квадрат, треугольник, ромб, прямоугольник.

Давайте разберемся, как построить фигуру, симметричную данной относительно прямой.

Пример 1. Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC относительно прямой.

1. Проведем из вершин треугольника ABC три прямые, перпендикулярные оси симметрии, выведем эти прямые на другую сторону оси симметрии.
2. Найдем расстояние от вершин треугольника ABC до точек на оси симметрии.
3. С другой стороны прямой отложим такие же расстояния.
4. Соединяем точки отрезками и строим треугольник A₁B₁C₁, симметричный треугольнику ABC.
5. Получаем два треугольника, симметричных относительно оси симметрии.

Пример 2. Постройте треугольник, симметричный треугольнику ABC относительно прямой d.

1. Строим по уже известному алгоритму. Проводим прямые из вершин треугольника ABC и выводим их на другую сторону оси симметрии.
2. Измеряем расстояние от вершин до точек на прямой.
3. Откладываем такие же расстояния на другой стороне оси симметрии.
4. Соединяем точки и строим треугольник A₁B₁C₁.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно прямой l.

1. Измеряем расстояние от точки B до прямой l и от точки A до прямой l.
2. Проводим прямую от точки А через прямую l под прямым углом к прямой l, выводя за ось симметрии.
3. Проводим прямую от точки B через прямую l под прямым углом к прямой l, выводя за ось симметрии.
4. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Центральная симметрия

Теперь поговорим о центральной симметрии — вот ее определение:

Центральной симметрией называется симметрия относительно точки.

Фигуры с центральной симметрией, как и фигуры с осевой симметрией, окружают нас повсюду. Центральную симметрию можно заметить в живой природе, в разрезе фруктов и в цветах на 8 марта.

Давайте разберемся, как построить центральную симметрию и рассмотрим алгоритм построения фигур с центральной симметрией.

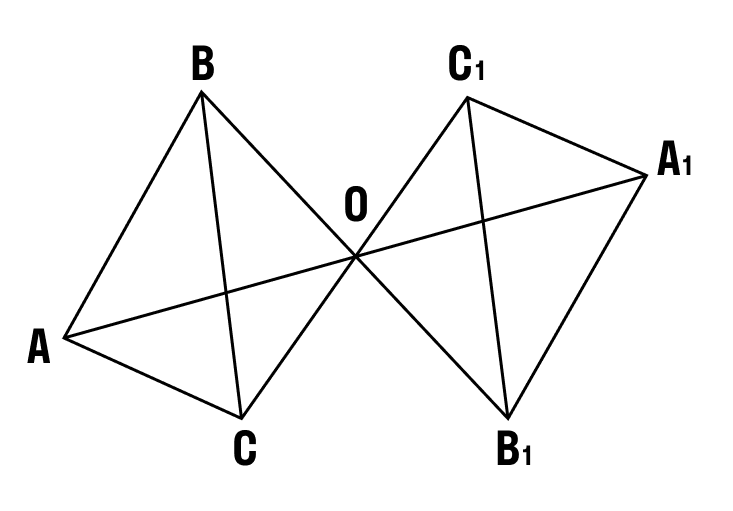
Пример 1: Постройте треугольник A₁B₁C₁ ,симметричный треугольнику ABC, относительно центра (точки О).

1. Соединяем точки ABC c центром и выводим эти прямые на другую сторону оси.
2. Измеряем отрезки AO, BO, CO и откладываем равные им отрезки с другой стороны от центра (точки О).
3. Получившиеся точки соединяем отрезками A₁B₁ A₁C₁ B₁C₁.
4. Получаем треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра.

Пример 2. Постройте треугольник A₁B₁C₁, симметричный треугольнику ABC, относительно центра (точки О).

1. По аналогии с предыдущим примером сначала соединяем точки ABC с точкой O.
2. Выводим прямые за точку О.
3. Измеряем отрезки AO, BO, CO и отмеряем такие же на противоположной стороне.
4. Получаем два центрально-симметричных треугольника.

Пример 3. Построить отрезок A₁B₁, симметричный отрезку AB относительно центра (точки О).

1. Измеряем расстояние от точки B до точки О и от точки А до точки О.
2. Проводим прямую из точки А через точку О и выводим ее на другую сторону.
3. Проводим прямую из точки B через точку О и выводим ее на другую сторону.
4. Чертим на противоположной стороне отрезки равные отрезкам АО и OB.
5. Соединяем точки A₁ и B₁ и получаем отрезок A₁B₁, симметричный данному.

Задачи на самопроверку

В 8 классе геометрия — сплошная симметрия: центральная, осевая, зеркальная да какая угодно. Чтобы во всем этом не поплыть, больше тренируйтесь. Чертите и приглядывайтесь, угадывайте вид симметрии и решайте больше задачек. Вот несколько упражнений для тренировки. Мы в вас очень верим!

Задачка 1. Рассмотрите симметричные геометрические рисунки и назовите вид симметрии.

Мы рассмотрели примеры осевой и центральной симметрии и знаем, что:

Симметрия относительно прямой — осевая
Симметрия относительно точки — центральная

Задачка 2. Пусть M и N какие-либо точки, l — ось симметрии. М₁ и N₁ — точки,
симметричные точкам M и N относительно прямой l. Докажите, что MN = М₁N₁.

Подсказка: опустите перпендикуляры из точек N и N₁ на прямую MМ₁.

Задачка 3. Постройте фигуру, симметричную данной относительно прямой a.

Источник