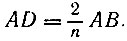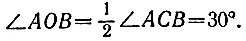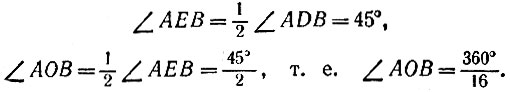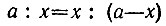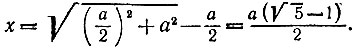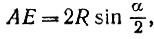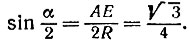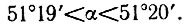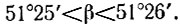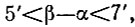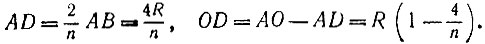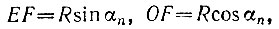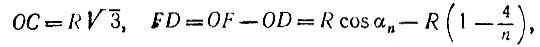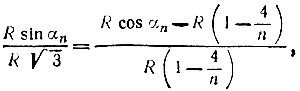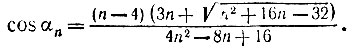Правильный пятиугольник построение способы

Пятиугольник

Здравствуйте коллеги.
Сегодня построим правильный пятиугольник в окружности, попробуем начертить циркулем и линейкой фигуру.

Рисунки художников очень тесно связаны с черчением и геометрией. Если мы задумали какую-то композицию, а в ней есть геометрические фигуры, то нам необходимо знать, как изобразить предмет, что бы он не выглядел смешно, и что бы вы не выглядели дилетантом и смогли нарисовать пятиконечную звезду циркулем или в фотошопе. От этого зависит ваш авторитет художника, а значит и заказы.

Построение правильного пятиугольника не так часто встречается в рисунке, но все же есть моменты, когда нам это необходимо.

Например, нам нужно нарисовать пятиконечную звезду (пентаграмму) для картины о Советском прошлом или о настоящем Китая. Правда для этого нужно уметь создать рисунок звезды в перспективе. Это посмотрите в другом уроке.

Мы попробуем нарисовать звезду в фотошопе фронтально. Точно так же вы сможете нарисовать фигуру карандашом на бумаге. Всего лишь с помощью таких инструментов:

Как правильно нарисовать звезду, что бы она выглядела ровно и красиво, сразу не ответишь. Количество углов не четное, поэтому просто разделить окружность на равные части циркулем или линейкой не получится.

Что бы вписанный пятиугольник в окружность был пропорциональный, нам необходимо точно вычислить одну из сторон, а затем отложить этот отрезок пять раз на теле овала.

Как выглядит пятиугольник и звезда

Внизу на фото разберем, как нарисовать звезду поэтапно.
Для начала рисуем окружность с центром О.

Дальше отложим отрезок OA равный радиусу и разделим его пополам точкой B, как показано на фото внизу.

Теперь от точки В до точки С проведем прямую.

Отложим расстояние отрезка ВС на диаметральной линии окружности. Для этого можно воспользоваться циркулем. Таким образом у нас появилась точка D.

И отрезок DB. Картинка внизу.

Дальше, проведя линию от точки D к точке С, Мы получи длину равную стороне пятиугольника.

Дальше этот отрезок можно отложить на окружности. У нас появилась точка Е. Смотрим фото ниже.

Итак, одна из сторон пятиугольника у нас есть, это линия ЕС.

Такие же отрезки наносим на всей части круга. Смотрим картинку.

На этом построение правильного пятиугольника можно закончить. Что бы нарисовать звезду нужно просто соединить углы через один.

Нарисовать пятиконечную звезду циркулем можно так же, как и на нашем уроке в программе Photoshop, весь процесс такой же, только вместо программы графического редактора используем инструменты для черчения.

Так же можно посмотреть уроки построения шестиугольника, разделение на восемь частей, деление круга на семь частей, десять равных частей.

Источник

Техническое черчение. Построение правильных многоугольников.

Построение вписанного в окружность правильного шестиугольника.

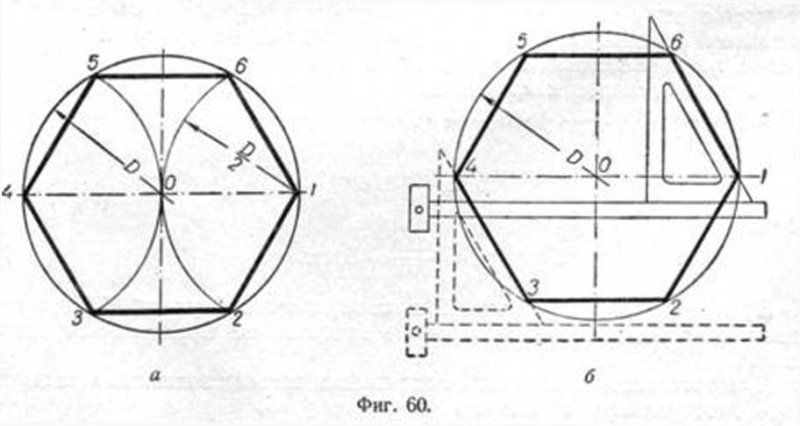
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой.

Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4, строим стороны 1 — 6, 4 — 3, 4 — 5 и 7 — 2, после чего проводим стороны 5 — 6 и 3 — 2.

Построение вписанного в окружность равностороннего треугольника.

Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля. Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.

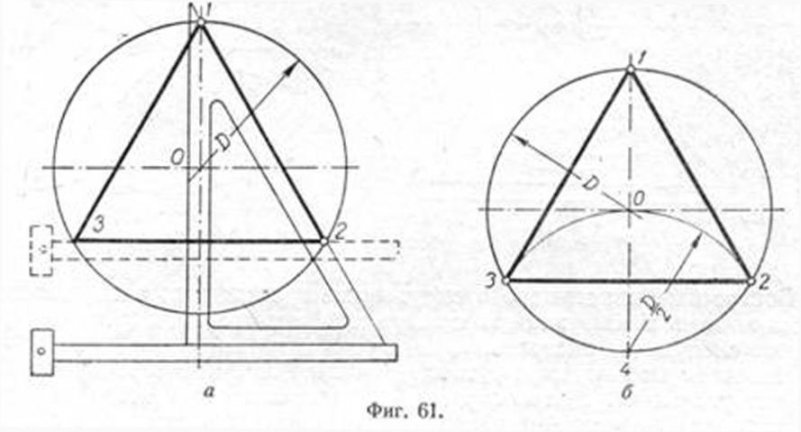
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0 — 1 — 2 равен 30°, то для нахождения стороны 1 — 2 достаточно построить по точке 1 и стороне 0 — 1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1 — 2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2 — 3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.

Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.

Для построения треугольника намечаем на диаметре вершину точку 1 и проводим диаметральную линию 1 — 4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.

Построение квадрата, вписанного в окружность.

Это построение можно выполнить при помощи угольника и циркуля.

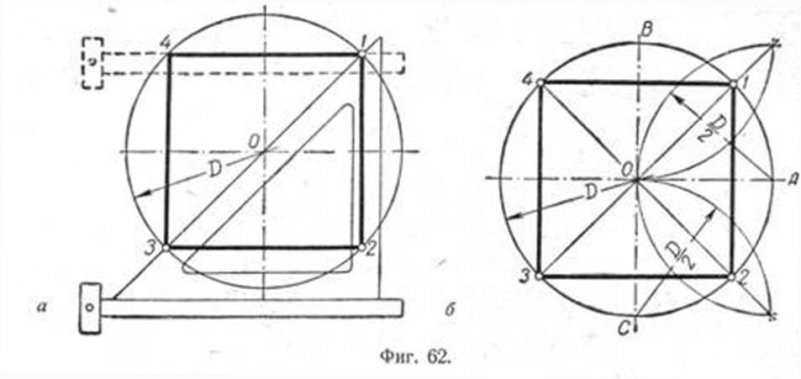
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4 — 1 и 3 —2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1 — 2 и 4 — 3.

Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра. Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.

Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.

Построение вписанного в окружность правильного пятиугольника.

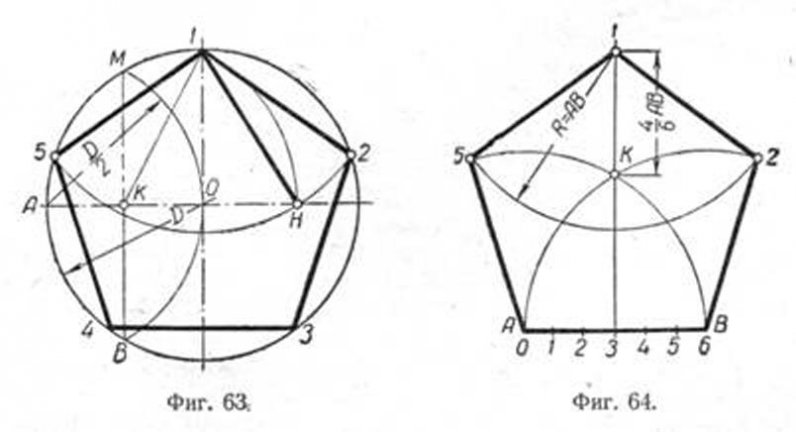
Чтобы вписать в окружность правильный пятиугольник, производим следующие построения. Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.

Построение правильного пятиугольника по данной его стороне.

Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую. Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB. Получим точку 1 —вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.

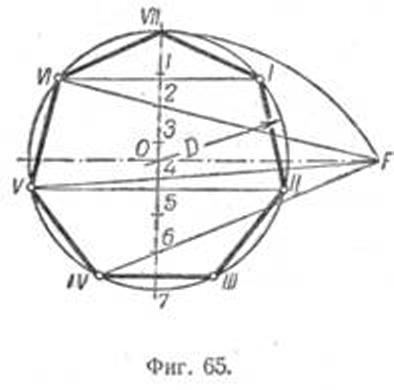
Построение вписанного в окружность правильного семиугольника.

Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.

Приведённый способ годен для построения правильных многоугольников с любым числом сторон.

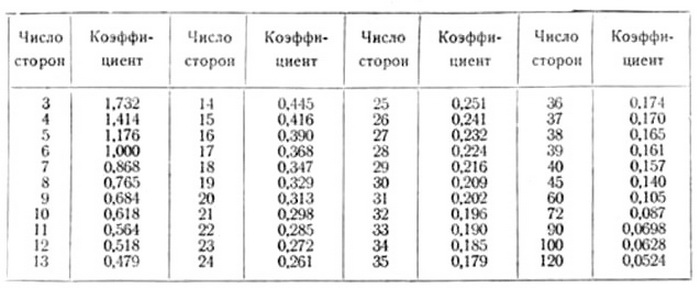
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.

Длины сторон правильных вписанных многоугольников.

В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй — коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника.

Источник

§ 15. Правильные многоугольники

Правильные многоугольники уже в глубокой древности считались символом красоты и совершенства. Это и понятно: ведь из всех многоугольников с заданным числом сторон наиболее приятен для глаза правильный многоугольник, у которого равны все стороны и равны все углы.

Практическая задача построения таких многоугольников с помощью циркуля и линейки имеет давнюю историю. Евклид в своем труде по геометрии приводит способы построения правильных треугольника, четырехугольника (квадрата), пятиугольника и пятнадцатиугольника, а также всех многоугольников, которые получаются из них удвоением числа сторон (не обязательно однократным). Следовательно, древние греки могли строить правильные многоугольники с числом сторон, равным

Долгое время математиков особенно занимал вопрос о построении правильного семиугольника. Лишь в 1796 г. К. Ф. Гаусc доказал принципиальную невозможность этого построения с помощью только циркуля и линейки. Более того, им было доказано, что среди правильных многоугольников с нечетным числом сторон построить можно только такие, для которых число сторон является либо простым числом вида 2 2 m + 1, m = 0, 1, 2, . (которых в настоящее время известно всего пять: 3, 5, 17, 257 и 65 537), либо произведением нескольких таких различных чисел. Таким образом, начатый выше список нельзя дополнить числами 7, 9, 11, 13, 14, а можно лишь продолжить следующим образом:

(заметим, что правильные многоугольники со слишком большим числом сторон по внешнему виду мало отличаются от обыкновенной окружности).

В настоящем параграфе мы предлагаем вам самим поискать способы построения правильных многоугольников, вписанных в данную окружность или имеющих заданную сторону. Не менее важное практическое значение имеют методы приближенного построения в тех случаях, когда точное построение циркулем и линейкой неосуществимо.

Докажите, что для построения правильного n-угольника, вписанного в данную окружность, достаточно разделить эту окружность на n равных частей и полученные точки деления последовательно соединить кордами. Как можно приближенно разделить окружность на заданное число равных дуг?

Дан правильный многоугольник, число сторон которого представляет собой произведение натуральных чисел k и m, где m>2. Как построить правильный m-угольник?

В окружность вписан правильный многоугольник. Постройте правильный многоугольник, у которого число сторон вдвое больше, чем у исходного.

Постройте правильный треугольник со стороной, равной заданному отрезку.

Впишите в данную окружность правильный шестиугольник.

Постройте правильный шестиугольник, со стороной, равной заданному отрезку.

Впишите в данную окружность правильный треугольник.

Постройте квадрат со стороной, равной заданному отрезку.

Впишите в данную окружность квадрат.

Впишите в данную окружность правильный восьмиугольник.

Впишите в данную окружность правильный двенадцатиугольник.

Впишите в данную окружность правильный шестнадцатиугольник.

Постройте правильный восьмиугольник со стороной, равной заданному отрезку.

Постройте правильный двенадцатиугольник со стороной, равной заданному отрезку.

Постройте правильный шестнадцатиугольник со стороной, равной заданному отрезку.

Разделите отрезок на такие две неравные части, чтобы квадрат большей из них был равен произведению длины всего отрезка и меньшей его части.

Докажите, что сторона правильного вписанного в окружность десятиугольника равна большей части «золотого сечения»;радиуса этой окружности. Впишите в данную окружность правильный десятиугольник.

Впишите в данную окружность правильный пятиугольник^

Как построить пятиконечную звезду?

Впишите в данную окружность правильный пятнадцатиугольник.

Постройте правильный пятиугольник со стороной, равной заданному отрезку.

Нарисуем окружность и впишем в нее правильный треугольник. Затем, начиная от одной его вершины, последовательно сделаем на окружности шесть засечек раствором циркуля, равным половине стороны треугольника, и построим семиугольник с вершинами в полученных шести точках и в исходной точке.

Насколько точен предложенный способ построения правильного семиугольника?

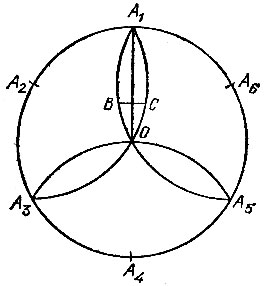
Проведем окружность большого радиуса G центром в точке О (рис. 47), которую разделим на шесть равных частей точками А₁, А₂, А₃, А₄, А₅, А₆. С центрами в точках А₂, А₄ и А₆ проведем дуги окружностей того же радиуса, образующие фигуру из трех «лепестков». Радиус А₁О разделим на три части и через ближайшую к точке О точку деления проведем прямую, перпендикулярную этому радиусу. Отрезок ее ВС, содержащийся внутри лепестка, примем за сторону десятиугольника, вписанного в окружность радиуса ОВ.

Рис. 47

Насколько точен предложенный способ построения правильного девятиугольника?

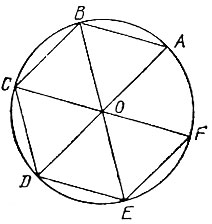
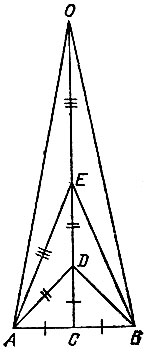
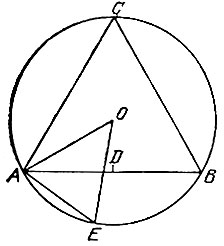
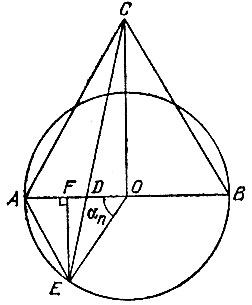
На диаметре АВ данной окружности как на стороне построим правильный треугольник АСВ (рис. 48). Возьмем на отрезке АВ точку D так, чтобы выполнялось равенство

Рис. 48

Продолжим отрезок CD до пересечения его о окружностью в точке Е. Хорду АЕ примем за сторону n-угольника, вписанного в данную окружность.

Насколько точен предложенный способ построения правильного n-угольника?

Решения

15.1. Если все я сторон вписанного я-угольника стягивают равные дуги окружности, то сами стороны равны между собой. Кроме того, в этом случае каждый из углов между соседними сторонами n-угольника является вписанным и опирается на дугу, составленную из n-2 упомянутых одинаковых дуг. Следовательно, все эти углы также равны между собой. Таким образом, задача построения вписанного правильного n-угольника сведена к делению окружности на я равных дур.

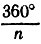
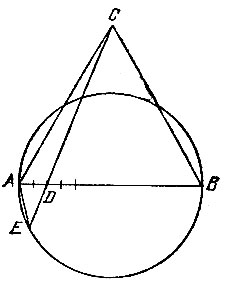
Если под рукой имеется транспортир, то с его помощью 360° можно начертить центральный угол, равный . Отложив один такой угол от какого-нибудь радиуса OA₁, мы получим радиус ОА₂. Отложив от него еще один такой же угол, мы получим следующий радиус OA₃ и т. д. Точки A₁, A₂, . A_n будут делить окружность на n частей, а уж в какой степени эти части окажутся равными, будет зависеть от точности, с которой откладывались требуемые центральные углы.

При отсутствии транспортира можно применить следующий способ приближенного деления окружности на заданное число n равных частей с помощью циркуля. Выберем раствор циркуля на глаз таким, чтобы он примерно соответствовал расстоянию между соседними вершинами будущего n-угольника, и отложим от любой точки А₆ на окружности n растворов циркуля в определенном направлении, получив последовательно точки A₁, A₂, . A_n. Если точки A₀ и А_n практически совпадают, то раствор циркуля выбран нами уже достаточно точно. Если же эти точки сколь-нибудь заметно различаются, то дугу A₀A_n разделим на n примерно равных частей и отметим ту точку деления A₀, которая расположена ближе всего к точке A₀ (рис. 49). Подправим раствор циркуля так, чтобы он соответствовал расстоянию между точками A’₀ и A’₁, и повторим все сначала, отложив n растворов циркуля от точки A’₀ и получив точки A’₁, A’₂, . A’_n. Сравнив точки A’₀ и A’_n, мы опять выясним, достаточно ли точным оказался раствор циркуля. Если еще нет, то подправим его еще раз и т. д. до тех пор, пока нужная точность не будет достигнута.

Рис. 49

15.2. Пусть A₁, A₂, . A_km — последовательные вершины исходного многоугольника. Тогда многоугольник с вершинами A₁, A₂, . A_km будет правильным, поскольку эти вершины лежат на одной окружности (описанной около исходного многоугольника) и делят ее на равные дуги.

15.3. Проведем к каждой стороне данного многоугольника свой серединный перпендикуляр до его пересечения о дугой окружности, стягиваемой этой стороной. Так как полученные точки пересечения разделят каждую из дуг на две равные части, то эти точки вместе с вершинами исходного многоугольника образуют вершины требуемого многоугольника.

15.4. Пусть АВ — заданный отрезок. Проведем две дуги окружностей с центрами в точках A и B и радиусом AВ до пересечения их в точке С. Соединив точки A и B с точкой С, получим требуемый правильный треугольник ABC.

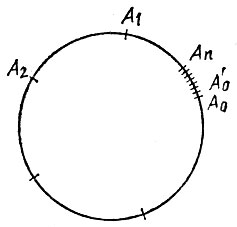
15.5. Возьмем на данной окружности с центром О произвольную точку A и раствором циркуля, равным ОА, отложим на окружности последовательно еще пять точек В, C, D, Е и F. Точки A, В, С, D, Е и F являются вершинами правильного шестиугольника. В самом деле, соединив эти точки последовательно друг с другом и с точкой О, мы получим пять равносторонних треугольников (рис. 50). Так как каждый из углов АОВ, ВОС, COD, DOE, EOF равен по 60°, то угол AOF также равен 60°, а, значит, окружность разделена на шесть равных дуг.

Рис. 50

15.6. Раствором циркуля, равным длине данного отрезка, проведем окружность. Вписав в эту окружность шестиугольник способом, предложенным в решении задачи 15.5, мы получим правильный шестиугольник с заданной стороной.

15.7. Разделим данную окружность на шесть равных частей (см. задачу 15.5) и точки деления через одну последовательно соединим хордами. Получим правильный треугольник (см. задачу 15.2).

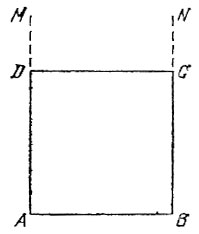
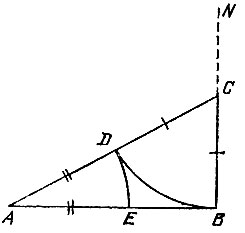
15.8. Из концов данного отрезка АВ восставим перпендикуляры AM и BN по одну сторону от отрезка АВ (рис. 51) и отложим на них соответственно отрезки AD и ВС, равные отрезку АВ, Соединив точки С и D, получим квадрат ADCB. В самом деле, четырехугольник ADCB является параллелограммом (ибо его стороны AD и ВС равны и параллельны), ромбом (ибо АВ = ВС) и прямоугольником (ибо ∠ ABC = 90°), а значит, квадратом.

Рис. 51

15.9. Через центр окружности проведем два взаимно перпендикулярных диаметра АС и BD и их концы последовательно соединим хордами. Получим вписанный квадрат ABCD. Действительно, дуги АВ, ВС, CD и AD равны между собой, поскольку на них опираются равные центральные углы в 90° каждый.

15.10. Впишем в данную окружность квадрат (см. задачу 15.9) и удвоим число его сторон (см. задачу 15.3).

15.11. Удвоив число сторон правильного вписанного в данную окружность шестиугольника, мы получим правильный двенадцатиугольник, вписанный в ту же окружность (см. задачи 15.5 и 15.3).

15.12. Удвоив число сторон правильного вписанного в данную окружность восьмиугольника, мы получим правильный шестнадцатиугольник, вписанный в ту же окружность (см. задачи 15.10 и 15.3).

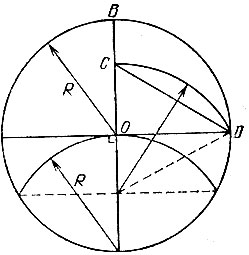
15.13. Из середины С данного отрезка АВ (рис. 52) восставим перпендикуляр и отложим на нем отрезок CD, равный 1 /₂ АВ. Затем на его продолжении отложим отрезок DO, равный AD. Тогда отрезок АО является радиусом окружности, описанной около правильного восьмиугольника со стороной АВ.

Рис. 52

В самом деле, найдем величину угла АОС. Так как АС = CD, то треугольник ACD равнобедренный, и так как он прямоугольный, то угол ADC равен 45°. Поскольку AD = DO, то треугольник ADO равнобедренный и угол AOD равен 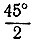и, следовательно, угол АОВ равен 45°, т. е. дуга АВ есть 1 /₈ часть окружности.

Теперь на окружности радиуса АО от любой точки последовательно отложим семь дуг, каждая из которых равна дуге АВ. Получим вершины правильного восьмиугольника.

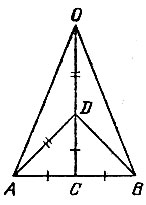
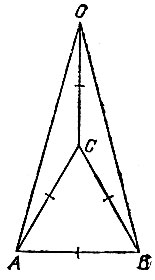
15.14. Построим равносторонний треугольник АСВ со стороной, равной данному отрезку АВ. Через точку С проведем прямую, перпендикулярную отрезку АВ. Отложим на этой прямой отрезок СО, равный АВ (рис. 53). Тогда отрезок АО является радиусом окружности, описанной около правильного двенадцатиугольника со стороной АВ. Для подтверждения этого достаточно доказать, что угол АОВ равен 30°. Точка С равноудалена от точек А, В и О, т. е. является центром окружности, описанной около треугольника АОВ. Поэтому

Рис. 53

Теперь на окружности радиуса AО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника.

15.15. Из середины С отрезка АВ восставим перпендикуляр (рис. 54) и на нем отложим отрезок CD9 равный 1 /₂ АВ, затем отрезок DE, равный AD, и отрезок ВО, равный АЕ. Тогда отрезок АО является радиусом окружности, описанной около правильного шестнадцатиугольника со стороной АВ.

Рис. 54

Так же как и в задаче 15.13, находим, что

Построение правильного шестнадцатиугольника выполняется аналогично построению в предыдущих задачах.

Теперь на окружности радиуса АО от любой точки последовательно отложим 15 дуг, каждая из которых равна дуге АВ. Получим вершины правильного шестнадцатиугольника.

15.16. Пусть заданный отрезок АВ имеет длину а. Найдем длину х большей части «золотого сечения» отрезка АВ. Из пропорции

Рис. 55

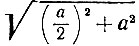
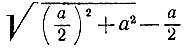
Следовательно, задача сводится к построению отрезка указанной длины х по отрезку длины а. Число равно длине гипотенузы прямоугольного треугольника с катетами а и а /₂, который можно построить с помощью циркуля и линейки. Для получения отрезка длины достаточно из гипотенузы построенного треугольника вычесть отрезок длины а /₂. Следовательно, построение «золотого сечения» отрезка АВ можно произвести следующим образом (рис. 55):

1. из точки В восставим перпендикуляр BN к отрезку АВ, на нем отложим отрезок ВС длины 1 /₂ АВ;
2. соединим точки А и С и отложим на отрезке АС отрезок DC длины ВС;
3. отложим на отрезке АВ отрезок АЕ длины AD, тогда точка Е делит отрезок АВ в «золотом сечении».

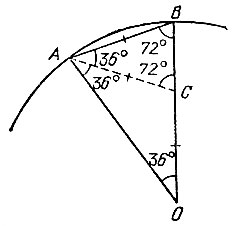
15.17. Пусть АВ — сторона правильного вписанного в окружность десятиугольника. Тогда ∠ AОВ = 36°, а каждый из углов ОАВ и АВО равен 72° (рис. 56). Проведем биссектрису АС угла A треугольника АОВ. Так как ∠ AСВ = 72°, то из равнобедренных треугольников ABC и АСО получим AB = AС = ОС.

Рис. 56

По свойству биссектрисы треугольника имеем ОС:ВС = АO:АВ. Поскольку АО = ОВ, АВ = ОС, то ОС:ВС = ОВ:ОС, т. е. ОС 2 = ВС*ОВ, а это и означает, что радиус ОВ разделен точкой С в «золотом сечении», причем ОС — большая часть радиуса (ибо ∠ ACB> ∠BAC, откуда ОС = АВ>ВС).

Таким образом, разделив радиус ОВ данной окружности в «золотом сечении» (см. задачу 15.16) и взяв большую его часть ОС, мы найдем длину стороны А В правильного вписанного в эту окружность десятиугольника. Теперь от любой точки данной окружности последовательно отложим девять хорд, каждая из которых равна АВ. Один из конкретных способов построения стороны ОС = АВ требуемого десятиугольника приведен на рис. 57.

Рис. 57

15.18. Разделим данную окружность на 10 равных частей (см. задачу 15.7). Тогда точки деления, взятые через одну, являются вершинами правильного пятиугольника (см. задачу 15.2). Впрочем, на рис. 57, где построен отрезок ОС, равный стороне правильного вписанного десятиугольника, имеется и отрезок CD, равный стороне требуемого пятиугольника.

15.19. Нарисуем некоторую окружность, разделим ее на 5 равных частей (см. задачу 15.18) и соединим точки деления через одну хордами друг с другом, как указано на рис. 58.

Рис. 58

15.20. Поскольку 1 /₆ — 1 /₁₀ = 1 /₁₅, то, отняв от дуги, равной 1 /₆ окружности, дугу, равную 1 /₁₀ окружности, мы получим остаток, равный 1 /₁₅ окружности. Это наблюдение позволяет вписать в окружность правильный пятнадцатиугольник (способы деления окружности на 6 и 10 частей описаны в задачах 15.5 и 15.17).

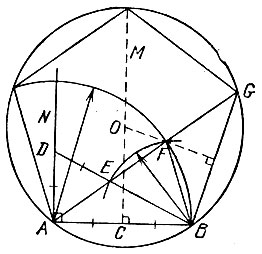
15.21. Из конца А и середины С заданного отрезка АВ восставим перпендикуляры АN и СМ и проведем окружность с центром А и радиусом АВ (рис. 59). Отложим на перпендикуляре AN отрезок AD длины АС и проведем отрезок BD. Отложим на отрезке BD отрезок DE длины AD и проведем окружность с центром В и радиусом BE до пересечения с первой окружностью в точке F. На прямой AF построим точку G на расстоянии АВ от точки В, Тогда центр О окружности, описанной около правильного пятиугольника со стороной АВ, лежит на пересечении прямой СМ с серединным перпендикуляром к отрезку BG. Действительно, окружность, описанная около треугольника ABG, является описанной и около требуемого пятиугольника, так как вписанный угол BAG равен центральному углу BAF, опирающемуся на сторону FB десятиугольника, вписанного в первую окружность (см. задачу 15.17), и, следовательно, равному 36°. Поэтому углы BOG и AOB равны 72° каждый. Остальные две вершины пятиугольника лежат на пересечениях описанной окружности с перпендикуляром СМ и с первой окружностью соответственно.

Рис. 59

15.22. Построенный семиугольник не является правильным. В самом деле, пусть О — центр окружности, точка D — середина стороны АВ правильного треугольника, а точка Е — первая из засечек, сделанных на окружности радиусом 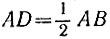(рис. 60). Найдем величину α угла АОЕ.

Рис. 60

Пусть R — радиус окружности, тогда 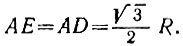Из равнобедренного треугольника АОЕ имеем

По таблицам синусов находим, что

Центральный угол β опирающегося на сторону правильного семиугольника равен 360° /₇, т. е.

Следовательно, построенный семиугольник не является правильным. Однако из приведенных неравенств следует,

а значит, в результате шести откладываний дуги АЕ на окружности погрешность построений хотя и будет накапливаться, но не превзойдет 6(β — α) 4 справедливы равенства

Рис. 62

Для угла 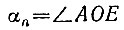имеем

а из подобия треугольников DOC и DFE получаем

откуда после преобразований находим

Подставляя в эту формулу значения n = 5, 7, 8, 9, 10, получаем следующие углы:

Сравнение с истинными значениями центральных углов, каковыми являются соответственно углы 72°, 51 3 /₇° ≈51°26′, 45°, 40°, 36°, показывает, что при n≤7 метод дает исключительно высокую точность, а с ростом n погрешность растет. Однако преимущество этого метода состоит в том, что его можно единообразно использовать при различных значениях n.

Источник

Читайте также:  Вычисли площадь фигуры реши задачу разными способами