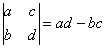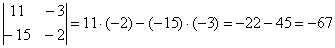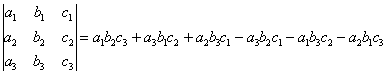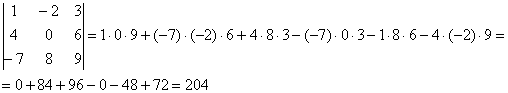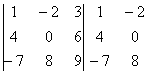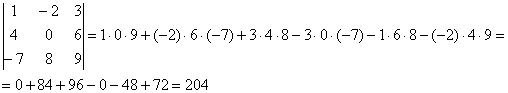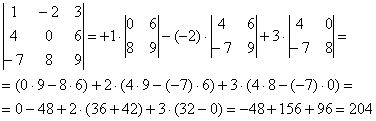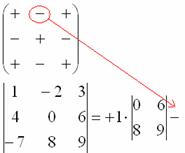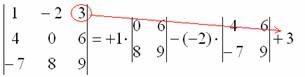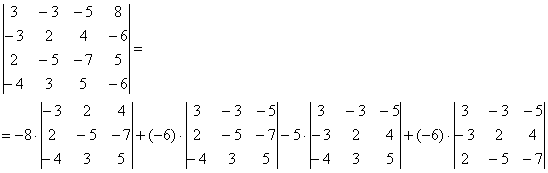Практический способ вычисления определителя

Как вычислить определитель?

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы. Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей, он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

Определитель можно вычислить только для квадратной матрицы (более подробно см. Действия с матрицами)

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .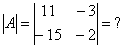

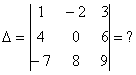
Определитель четвертого порядка 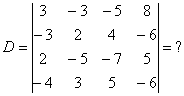тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

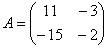
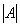
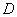
Обозначения: Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса 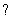в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два»:

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 — нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

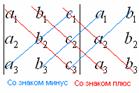
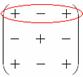
Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу.
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

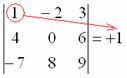
В следующем примере будем раскрывать определитель по первой строке.
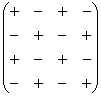
Для этого нам понадобится матрица знаков: 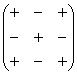. Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот: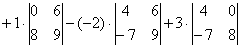
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ. Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке, очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент: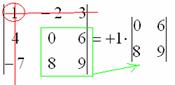

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

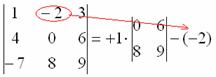
4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент: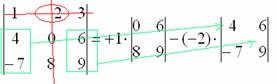

Оставшиеся четыре числа записываем в маленький определитель.

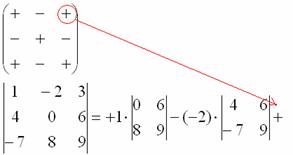
Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент: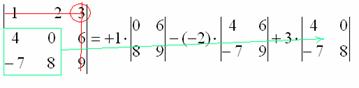

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу:

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя.

Автор: Емелин Александр

(Переход на главную страницу)

«Всё сдал!» — онлайн-сервис помощи студентам

Источник

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Вспомогательная страница к разделу ОПРЕДЕЛИТЕЛЬ

Приемы вычисления определителей, зависящих от параметров

Довольно часто на практике возникает необходимость вычислять определители, элементы которых зависят от параметров. Метод Гаусса оказывается не слишком приспособленным для такой задачи.

Пример. Вычислить

Решение. Разложение по общей формуле даст величину этого определителя в виде полинома от $ <\color\alpha > $. С другой стороны, если для его вычисления мы попытаемся применить метод Гаусса, то на первом же шаге элементы преобразованного определителя окажутся дробно–рациональными функциями от параметра $ <\color\alpha > $. Понятно, что после приведения определителя к треугольному виду и перемножения стоящих на диагонали дробей мы, в конце концов, получим тот же ответ полиномиального вида, но сам факт, что для его получения потребовалось «выйти за пределы» множества полиномиальных функций не свидетельствует в пользу метода Гаусса… ♦

Выделение линейных множителей

Этот прием основан на свойстве полиномиальности определителя как функции его элементов. Если элементы зависят — также полиномиально — от одного параметра, то можно попытаться определить линейные множители «полинома из ответа»: иногда из особенностей определителя очевидно при каких значениях параметра этот определитель обращается в нуль.

Пример. Вычислить определитель

$$\left|\begin 1&1&1&\dots&1\\ 1&2-x&1&\dots&1\\ 1&1&3-x&\dots&1\\ \vdots& & &\ddots&\vdots\\ 1&1&1&\dots&n+1-x \end\right|.$$

Решение. Ответом в этой задаче должен быть полином по $ x_<> $. Обозначим его $ F(x)_<> $ и попробуем догадаться какие корни он может иметь. Обратим внимание на структуру определителя. Если положить $ x=1_<> $, то вторая строка будет одинаковой с первой, на основании свойства 3 определителя, при этом значении $ x_<> $ будем иметь $ F(1)=0 $. Аналогично убеждаемся, что $ F(2)=0, \dots, F(n)=0 $. Итак, на основании теоремы Безу, имеем: $$ F(x) \equiv F_1(x) (x-1)\times \dots \times (x-n) \ , $$ где через $ F_1(x) $ обозначен полином, являющийся частным от деления $ F(x)_<> $ на произведение линейных множителей. Оценим степень полинома $ F(x)_<> $. Очевидно, что при разложении определителя по общей формуле из определения, каждое слагаемое представляет произведение элементов определителя и будет полиномом по $ x_<> $. В каждом слагаемом максимально возможная степень может быть достигнута если каждый элемент в произведении будет иметь максимально возможную степень — в нашем случае равную $ 1_<> $. Отсюда с неизбежностью следует, что самым «большим» по степени может быть только главный член определителя, т.е. произведение элементов его главной диагонали: $$ F(x) \equiv 1\cdot (2-x)\times \dots \times (n+1-x) + \dots \ , $$ где многоточия скрывают все оставшиеся слагаемые полного разложения определителя и имеют степени меньшие степени выделенного слагаемого. Выделяем из этого слагаемого степень $ x_<> $: $$ F(x) \equiv (-1)^n x^n + \dots \ . $$ Мы получили оценку степени $ F(x)_<> $ вместе с выражением для его старшего коэффициента.

Ответ. $ (-1)^ (x-1)\times \dots \times (x-n) $.

Пример. Вычислить определитель

Решение. Если к первому столбцу прибавить остальные, то обнаружится, что определитель делится на $ x+y+z $; если к первому столбцу прибавить второй и вычесть третий и четвертый, то выделится множитель $ y+z-x $; если к первому столбцу прибавить третий и вычесть второй и четвертый, то выделится множитель $ x-y+z $; наконец, если к первому столбцу прибавить четвертый и вычесть второй и третий, то выделится множитель $ x+y-z $. Считая $ x,y,z $ независимыми переменными, заключаем, что все эти четыре множителя попарно взаимно просты, и значит, определитель — как полином от $ x,y,z $ — делится на их произведение $ (x+y+z)(y+z-x)(x-y+z)(x+y-z) $.

Это произведение содержит член $ z^4 $ с коэффициентом $ (-1) $, а сам определитель содержит тот же член с коэффициентом $ +1 $. Следовательно, $$ D=-(x+y+z)(y+z-x)(x-y+z)(x+y-z) =x^4+y^4+z^4-2x^2y^2-2x^2z^2-2y^2z^2 \ . $$

Метод рекуррентных соотношений

Основная идея метода заключается в том, что некоторые определители можно свести к вычислению определителей, имеющих аналогичный вид, но меньший порядок. Если удается установить вид этой зависимости в виде явной формулы, то эта формула — последовательным ее применением — позволит нам «спуститься» к определителям малых порядков.

Пример. Вычислить определитель

$$D_n=\left|\begin a_1&x&x&\dots&x\\ x&a_2&x&\dots&x\\ x&x&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ x&x&x&\dots&a_n \end\right|.$$

Решение. Представив элемент в правом нижнем углу в виде $ a_n=x+(a_n-x) $, можем определитель $ D_n $ разбить на сумму двух определителей: $$D_n=\left|\begin a_1&x&x&\dots&x\\ x&a_2&x&\dots&x\\ x&x&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ x&x&x&\dots&x \end\right|+\left|\begin a_1&x&x&\dots&0\\ x&a_2&x&\dots&0\\ x&x&a_3&\dots&0\\ \vdots&&&\ddots&\vdots\\ x&x&x&\dots&a_n-x \end\right|.$$ В первом определителе последний столбец вычтем из остальных, а второй определитель разложим по последнему столбцу: $$D_n=x(a_1-x)(a_2-x)\times\dots\times(a_-x)+(a_n-x)D_\ .$$ Это и есть рекуррентное соотношение. Подставляя в него аналогичное выражение для $ D_ $, найдем $$\begin D_n=x(a_1-x)(a_2-x)\times\dots\times(a_-x)+\\ +x(a_1-x)(a_2-x)\times\dots\times(a_-x)(a_n-x)+D_(a_-x)(a_n-x). \end$$ Повторяя то же рассуждение $ n-1 $ раз и замечая, что $ D_1=a_1=x+(a_1-x) $, найдем $$\begin D_n=x(a_1-x)(a_2-x)\dots(a_-x)+x(a_1-x)\times\dots\times(a_-x)(a_n-x)+\dots+\\ +x(a_2-x)\times\dots\times(a_n-x)+(a_1-x)(a_2-x)\times\dots\times(a_n-x)=\\ \displaystyle =x(a_1-x)(a_2-x)\times\dots\times(a_n-x)\left( \frac<1>+\frac<1>+\dots+\frac<1>\right). \end$$

$$\left|\begin a_1b_1&a_1b_2&a_1b_3&\dots&a_1b_n\\ a_1b_2&a_2b_2&a_2b_3&\dots&a_2b_n\\ a_1b_3&a_2b_3&a_3b_3&\dots&a_3b_n\\ \vdots&&&&\vdots\\ a_1b_n&a_2b_n&a_3b_n&\dots&a_nb_n \end\right|.$$

Ответ. $ \displaystyle a_1b_n\prod_^(a_b_j-a_jb_) $ .

Пример. Вычислить определитель

$$D_n=\left|\begin a_1&x&x&\dots&x\\ y&a_2&x&\dots&x\\ y&y&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ y&y&y&\dots&a_n \end\right|.$$

Решение начинается тем же приемом, что и в предыдущем примере: $$ D_n= \left|\begin a_1&x&x&\dots&x\\ y&a_2&x&\dots&x\\ y&y&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ y&y&y&\dots&x \end\right|+(a_n-x)D_=x(a_1-y)(a_2-y)\times \dots \times (a_-y)+(a_n-x)D_ \ . $$ Можно было бы идти по проторенному пути и «разделывать» определитель $ D_ $ с использованием уже полученной формулы. Имеется, однако, более эффективный прием. Заметим, что начальный определитель симметричен относительно вхождения параметров $ x_<> $ и $ y_<> $, и эта симметрия должна проявляться в окончательном ответе. Следовательно, наряду с полученным выражением, будет справедливо и следующее: $$ D_n=y(a_1-x)(a_2-x)\times \dots \times (a_-x)+(a_n-y)D_ \ , $$ произведенное перестановкой параметров $ x \leftrightarrow y $. В результате мы получаем систему уравнений для определения двух неизвестных величин $ D_ $ и $ D_ $. Решаем эту систему относительно $ D_n $ (например, по формулам Крамера): $$ D_n = \frac<\displaystyle y\prod_^n(a_k-x)-x\prod_^n(a_k-y)> \ . $$ ♦

В примере следующего пункта метод рекуррентных соотношений комбинируется с методом выделения линейных множителей.

Определитель Вандермонда

Подробнее о матрице, определителе Вандермонда и их применении ☞ ЗДЕСЬ.

Пример. Вычислить определитель Вандермонда

$$ V(x_1,\dots,x_n)= \left|\begin 1 &x_1&x_1^2&\ldots&x_1^\\ 1 &x_2&x_2^2&\ldots&x_2^\\ \vdots& &&& \vdots\\ 1 &x_n&x_n^2&\ldots&x_n^ \end\right|_ $$

Решение. Поясним идею для случая $ n=4 $. Выражение для $ V(x_1,x_2,x_3,x_4) $ — если его формально разложить по общей формуле — будет полиномом относительно своих переменных. Рассмотрим его как полином от переменной $ x_4 $, которую — для удобства — временно переобозначим через $ x $: $$ \tilde V(x)=\left|\begin 1 &x_1&x_1^2&x_1^3\\ 1 &x_2&x_2^2&x_2^3\\ 1 &x_3&x_3^2&x_3^3\\ 1 &x&x^2&x^3\\ \end\right| \ ; $$ оставшиеся переменные будем считать параметрами. Если подставить в этот определитель $ x=x_1 $, то определитель обратится в нуль (как имеющий одинаковые строки см. свойство 3 ☞ ЗДЕСЬ). Аналогичные рассуждения верны для $ x=x_2 $ и $ x=x_3 $. Таким образом, полином $ \tilde V(x) $ имеет корни $ x_1,x_2,x_3 $, а его степень — если разложить по последней строке — не превышает $ 3 $. Следовательно, этот полином должен иметь следующее разложение на линейные множители: $$ \tilde V(x) \equiv A(x-x_1)(x-x_2)(x-x_3) \ ; $$ при этом константа $ A $ зависит только от $ x_1, x_2,x_3 $. Выражение для нее можно найти, если сообразить, что она является старшим коэффициентом полинома $ \tilde V(x) $, т.е. коэффициентом при степени $ x^3 $. Этот коэффициент можно «извлечь» из исходного определителя — это алгебраическое дополнение элемента определителя, стоящего в правом нижнем углу, т.е. $$ \left|\begin 1 &x_1&x_1^2\\ 1 &x_2&x_2^2\\ 1 &x_3&x_3^2 \end\right| \ . $$ Но этот определитель — тот же определитель Вандермонда, только порядка меньшего исходного. Возвращая переменной $ x $ ее исходное значение, получаем рекуррентное соотношение: $$ V(x_1,x_2,x_3,x_4)\equiv V(x_1,x_2,x_3) (x_4-x_1)(x_4-x_2)(x_4-x_3) \ . $$ Раскладываем определитель в правой части по той же схеме: $$ V(x_1,x_2,x_3) \equiv \left|\begin 1 &x_1\\ 1 &x_2 \end\right| (x_3-x_1)(x_3-x_2) \equiv (x_3-x_1)(x_3-x_2)(x_2-x_1) \ . $$ Таким образом, $$ V(x_1,x_2,x_3,x_4)= $$ $$ =(x_2-x_1)(x_3-x_1)(x_3-x_2)(x_4-x_1)(x_4-x_2)(x_4-x_3) \ . $$ А в общем случае получаем ответ $$ V(x_1,\dots,x_n)= \prod_<1\le j ♦

Определитель трёхдиагональной матрицы

Более сложный пример применения метода дает задача вычисления определителя трехдиагональной матрицы, представленного в следующем виде (определитель Якоби):

$$ <\mathfrak J>_n = \left|\begin a_1 &b_1&0&0& \dots & 0 & 0\\ -c_2 &a_2&b_2&0& \dots & 0 & 0\\ 0 &-c_3&a_3&b_3& \dots & 0 & 0\\ \vdots &&& &\ddots&& \vdots \\ 0 &0&0&0& \dots & a_ & b_\\ 0 &0&0&0& \dots & -c_n & a_ \end\right|_ \ . $$ Формальное вычисление этого определителя (в соответствии с определением) даст полином по $ a_1,\dots,a_n,b_1,\dots,b_,c_2,\dots,c_n $, линейный по каждой из этих переменных. Если разложить $ <\mathfrak J>_n $ по последней строке, то получим: $$ \begin <\mathfrak J>_n&=&a_n<\mathfrak J>_+b_c_n<\mathfrak J>_ =a_n(a_<\mathfrak J>_+b_c_<\mathfrak J>_)+ b_c_n<\mathfrak J>_= \\ &=&(a_na_+b_c_n)<\mathfrak J>_+a_nb_c_<\mathfrak J>_= \dots \end $$

Пример.

$ <\mathfrak J>_2=a_1a_2+b_1c_2 $ , $ <\mathfrak J>_3=a_1a_2a_3+a_1b_2c_3+b_1c_2a_3 $, $$ <\mathfrak J>_5=a_1a_2a_3a_4a_5+b_1c_2a_3a_4a_5+a_1b_2c_3a_4a_5+a_1a_2b_3c_4a_5 +a_1a_2a_3b_4c_5+b_1c_2b_3c_4a_5+b_1c_2a_3b_4c_5+a_1b_2c_3b_4c_5 \ . $$

Теорема. Значение $ <\mathfrak J>_n $ равно сумме главного члена $ a_1a_2\times \dots \times a_ $ и всевозможных произведений, получающихся из него заменой одной или нескольких пар соседних множителей $ a_ja_ $ на $ b_jc_ $.

Частный случай определителя Якоби — континуант: $$ Q_n(x_1,x_2,\dots,x_) = \left|\begin x_1 &1&0&0& \dots & 0 & 0\\ -1 &x_2&1&0& \dots & 0 & 0\\ 0 &-1&x_3&1& \dots & 0 & 0\\ \vdots &&& &\ddots&&\vdots \\ 0 &0&0&0& \dots & x_ & 1\\ 0 &0&0&0& \dots & -1 & x_ \end\right|_ $$

Теорема. Континуант равен сумме произведения $ x_1\cdot x_2 \times \dots \times x_n $ и всевозможных произведений, получающихся из него вычеркиванием пар соседних множителей (и добавлением $ 1 $ в случае четного $ n $).

Пример.

$$ \begin Q_2(x_1,x_2)&=&x_1x_2+1 \ , \\ Q_3(x_1,x_2,x_3)&=& x_1x_2x_3+x_3+x_1 \ , \\ Q_6(x_1,x_2,x_3,x_4,x_5,x_6)&=&x_1x_2x_3x_4x_5x_6+\\ &&+x_3x_4x_5x_6 +x_1x_4x_5x_6+ x_1x_2x_5x_6+ x_1x_2x_3x_6+x_1x_2x_3x_4+ \\ &&+x_5x_6+x_1x_6+x_1x_2+x_1x_4+x_3x_4+x_3x_6+1 . \end $$

Исследуем еще один частный случай определителя Якоби — при одинаковых элементах на диагоналях $$a_1=\dots=a_n = a, \ b_1=\dots=b_ = b, \ c_2=\dots=c_n = c \ ; $$ таким образом: $$ <\mathfrak J>_n= \left|\begin a &b&0&0& \dots & 0 & 0\\ c &a&b&0& \dots & 0 & 0\\ 0 &c&a&b& \dots & 0 & 0\\ \vdots &&& &\ddots&& \vdots \\ 0 &0&0&0& \dots & a & b\\ 0 &0&0&0& \dots & c & a \end\right|_ \ . $$ В этом случае уравнение, связывающее определители трех последовательных порядков, принимает вид: $$ <\mathfrak J>_n=a<\mathfrak J>_-bc<\mathfrak J>_ \ .$$ Оно может быть решено применением общего приема решения линейного разностного уравнения.

Пример. Вычислить

$$ \left|\begin 2 &2&0& \dots & 0 & 0\\ 1 & 2 &2& \dots & 0 & 0\\ 0 &1&2& \dots & 0 & 0\\ \vdots && \ddots &\ddots&& \vdots\\ 0 &0&0& \dots & 2 & 2\\ 0 &0&0& \dots & 1 & 2 \end\right|_ \ . $$

Решение. Разностное уравнение имеет вид $ <\mathfrak J>_n=2<\mathfrak J>_-2<\mathfrak J>_ $. Cтроим соответствующее ему характеристическое уравнение и находим его корни: $ \lambda_<1,2>=1 \pm \mathbf i $. Поскольку они различны, решение разностного уравнения ищем в виде $$ C_1 (1+\mathbf i )^n+C_2 (1-\mathbf i)^n \ .$$ Для определения констант $ C_1 $ и $ C_2 $ вычислим определители первого и второго порядков: $ <\mathfrak J>_1=2,<\mathfrak J>_2=2 $. $$ \left\< \begin 2&=&C_1(1+\mathbf i)&+C_2(1+\mathbf i), \\ 2&=&C_1(1+\mathbf i)^2&+C_2(1+\mathbf i)^2 \end \right. \quad \Rightarrow \quad C_1=\frac<1-\mathbf i><2>,\ C_2=\frac<1+\mathbf i> <2>$$ Ответ. $ <\mathfrak J>_n=(1+\mathbf i)^+(1-\mathbf i)^ $.

Представление определителя в виде суммы определителей

Пример. Вычислить определитель

$$D_n=\left|\begin a_1+b_1&a_1+b_2&\dots&a_1+b_n\\ a_2+b_1&a_2+b_2&\dots&a_2+b_n\\ \dots&&&\dots\\ a_n+b_1&a_n+b_2&\dots&a_n+b_n \end\right|.$$

Решение. Определитель раскладывается по первой строке на два определителя, каждый из них по второй строке снова раскладывается на два определителя и т.д. Дойдя до последней строки, получим $ 2^n $ определителей.

Если при каждом разложении за первые слагаемые принимать числа $ a_i $, а за вторые — числа $ b_j $, то строки полученных определителей будут либо вида $ (a_i,a_i,\dots,a_i) $, либо вида $ (b_1,b_2,\dots,b_n) $. Две строки первого типа пропорциональны, а второго типа равны. При $ n>2 $ в каждый получившийся определитель попадут по крайней мере две строки одного типа, и он обратится в нуль. Таким образом, $$D_n=0 \ npu \ n>2,\ D_1=a_1+b_1,\quad D_2=\left|\begin a_1&a_1\\ b_1&b_2 \end\right|+\left|\begin b_1&b_2\\ a_2&a_2 \end\right|=(a_1-a_2)(b_2-b_1).$$

Вычислить определитель методом представления его в виде суммы определителей

$$\left|\begin x_1&a_1b_2&a_1b_3&\dots&a_1b_n\\ a_2b_1&x_2&a_2b_3&\dots&a_2b_n\\ a_3b_1&a_3b_2&x_3&\dots&a_3b_n\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ a_nb_1&a_nb_2&a_nb_3&\dots&x_n \end\right|.$$

Ответ. $$(x_1-a_1b_1)(x_2-a_2b_2)\times \dots \times (x_n-a_nb_n) \times $$ $$ \times \left(1+\frac+\frac+\dots+\frac\right) \ .$$

Увеличение порядка определителя

Пример. Вычислить определитель

$$ \det \left[ s_x-s_ \right]_^ = \left| \begin s_0x-s_1&s_1x-s_2&\dots& s_x-s_ \\ s_1x-s_2&s_2x-s_3&\dots& s_x-s_ \\ \dots & & & \dots \\ s_x-s_ & s_x-s_ & \dots & s_<2n-2>x-s_ <2n-1>\end \right|_ $$ при заданных числовых значениях $ s_0,s_1,\dots,s_ <2n-1>$.

Интерполяция

Можно считать излагаемый ниже метод обобщением приведенного выше метода выделения линейных множителей: если матрица имеет полиномиальную зависимость от параметра (параметров), то угадать корни ее определителя — также полинома от этого параметра — удается не всегда, а вот его значения при конкретных величинах параметра (параметров) всегда можно вычислить.

Попробуем решить пример, с которого начинается настоящий раздел.

Пример. Вычислить

$$ \det A(\alpha)= \left| \begin \alpha+1 &\alpha^2+1 &\alpha^2-1 &\alpha \\ \alpha^2+\alpha+1 & \alpha^2-\alpha+1 & \alpha^2 & 1 \\ 2\,\alpha+1 &\alpha^2+2 & \alpha & \alpha^2-1 \\ 2\,\alpha & 2\, \alpha^2+2\,\alpha+1 & \alpha^2-\alpha-1 & \alpha+1 \end \right| \ . $$

Решение. Поскольку каждый элемент определителя является полиномом, то, на основании определения определителя как суммы произведений его элементов, величина определителя также должна быть полиномом по $ \alpha_<> $. Обозначим этот полином через $ F(\alpha) $. Таким образом, задача сводится к вычислению степени $ \deg F $ этого полинома и его коэффициентов. Для решения первой задачи формируем новый определитель, путем вытаскивания из элементов исходного определителя их старших мономов: $$ \left| \begin \alpha &\alpha^2 &\alpha^2 &\alpha \\ \alpha^2 & \alpha^2 & \alpha^2 & 1 \\ 2\,\alpha &\alpha^2 & \alpha & \alpha^2 \\ 2\,\alpha & 2\, \alpha^2 & \alpha^2 & \alpha \end \right| \ . $$ Если этот определитель не равен нулю тождественно по $ \alpha_<> $, то его старший моном совпадает со старшим мономом $ F(\alpha) $. Новый определитель также зависит от $ \alpha_<> $, но характер этой зависимости становится менее сложным, чем у исходного, и для его вычисления можно использовать различные упрощающие соображения. Например, можно вынести общие множители элементов первого, второго и третьего столбцов (см. свойство 4 ☞ ЗДЕСЬ ) $$ =\alpha\cdot \alpha^2 \cdot \alpha \left| \begin 1 &1 & \alpha &\alpha \\ \alpha & 1 & \alpha & 1 \\ 2 &1 & 1 & \alpha^2 \\ 2 & 2 & \alpha & \alpha \end \right| = $$ Далее, вычитаем из последней строки первую, умноженную на $ 2_<> $: $$ =\alpha^4 \left| \begin 1 &1 & \alpha &\alpha \\ \alpha & 1 & \alpha & 1 \\ 2 &1 & 1 & \alpha^2 \\ 0 & 0 & -\alpha & -\alpha \end \right| =-\alpha^5 \left| \begin 1 &1 & \alpha &\alpha \\ \alpha & 1 & \alpha & 1 \\ 2 &1 & 1 & \alpha^2 \\ 0 & 0 & 1 & 1 \end \right| $$ Теперь вычтем из четвертого столбца третий: $$ =-\alpha^5 \left| \begin 1 &1 & \alpha & 0 \\ \alpha & 1 & \alpha & 1-\alpha \\ 2 &1 & 1 & \alpha^2 -1 \\ 0 & 0 & 1 & 0 \end \right| $$ и разложим определитель по последней строке: $$ = \alpha^5 \left| \begin 1 &1 & 0 \\ \alpha & 1 & 1-\alpha \\ 2 &1 & \alpha^2 -1 \\ \end \right| \ . $$ Поскольку нас интересует только лишь старший моном этого определителя, в элементах последнего столбца оставляем старшие мономы: $$ \alpha^5 \left| \begin 1 &1 & 0 \\ \alpha & 1 & -\alpha \\ 2 &1 & \alpha^2 \end \right| = \alpha^6 \left| \begin 1 &1 & 0 \\ \alpha & 1 & -1 \\ 2 &1 & \alpha \end \right| \ . $$ Этот определитель можно вычислить «вручную» (при этом, повторюсь, нас интересуют только лишь максимальные по степени $ \alpha_<> $ члены его разложения), получаем: $ — \alpha^8 $.

Итак, неизвестный полином $ F(\alpha) $ имеет степень $ 8_<> $. Для его определения у нас имеется представление этого полинома в форме определителя. При этом считается, что числовые определители мы вычислять умеем. Будем искать полином $ F(\alpha) $ как решение задачи интерполяции. Зададим произвольные числовые значения для $ \alpha_<> $ — в количестве $ 9_<> $ штук (по числу коэффициентов полинома, требующих определения), вычислим соответствующие числовые определители, составим интерполяционную таблицу: $$ \begin \alpha & \alpha_1 & \alpha_2 & \dots & \alpha_9 \\ \hline F & \det A (\alpha_1) &\det A (\alpha_2) & \dots & \det A (\alpha_9) \end $$ и вычислим $ F(\alpha) $ по одному из методов вычисления интерполяционного полинома.

На виду лежат два соображения:

1. имеет смысл в качестве чисел $ \alpha_j $ выбирать возможно минимальные по модулю;

2. поскольку мы уже знаем величину одного из коэффициентов, имеет смысл выбрать — из двух стандартных представлений интерполяционного полинома — форму Ньютона (последнее вычисление делать не придется, можно сократить число узлов интерполяции). Для настоящего примера: $$ \begin \alpha & 0 & 1 & -1 & 2 & -2 & 3 & -3 & 4 \\ \hline F & -4 & -4 & 24 &-222 & 734 & -9616 & 4388 & -98176 \end $$

Ответ. $ -\alpha^8-3\,\alpha^7+3\,\alpha^6-\alpha^5+23\,\alpha^4-7\,\alpha^3-11\,\alpha^2-3\,\alpha-4 $.

$$ B=\left( \begin 1 &2 &2 &1 \\ 2 &2 &2 & 0 \\ 1 &2 &1 & 2 \\ 1 & 2 & 2 & 1 \end \right) \ . $$ Требуется выбрать по одному элементу из каждой строки и каждого столбца этой матрицы, так, чтобы получившаяся сумма стала максимальной: $$ b_<1j_1>+b_<2j_2>+b_<3j_3>+b_ <4j_4>\quad \mbox < при различных >\quad \ < j_1,j_2,j_3,j_4\>\subset \ < 1,2,3,4 \>. $$ Иными словами, после выбора какого-то кандидата в сумму, из матрицы вычеркиваются строка и столбец его содержащие, и дальнейший выбор осуществляется в оставшейся подматрице. Задача оказывается нетривиальной уже хотя бы потому, что «жадная стратегия» выбора — когда на каждом шаге выбирается максимальный из оставшихся элементов — не приводит к правильному ответу: $$ B=\left( \begin 4 &3 \\ 3 &1 \end \right) \quad \Rightarrow \quad 4+1 1) .

Задача. Имеется $ n_<> $ работ, которые надо поручить $ n_<> $ работникам. Каждый работник может быть назначен только на одну работу, и каждая работа может быть поручена только одному работнику. Прибыль от труда работника под номером $ j_<> $ при выполнении работы под номером $ k_<> $ известна и равна $ b_ $. Как распределить работы между работниками так, чтобы прибыль стала максимальной?

Разные определители, встречающиеся в ресурсе

Источник