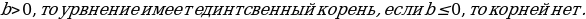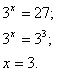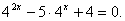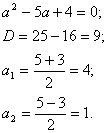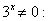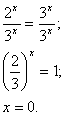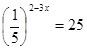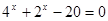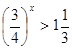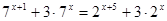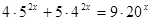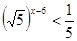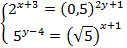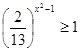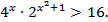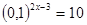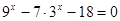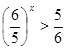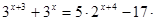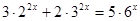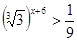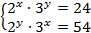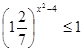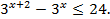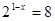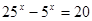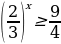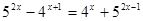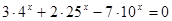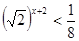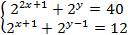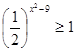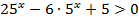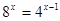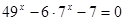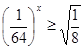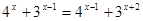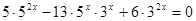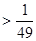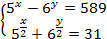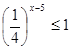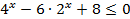Практическая работа показательные уравнения способы

Практическая работа по теме «показательные уравнения»

Раздел программы : Математиа

Тема : Уравнения. Неравенства

Тема практического занятия: Показательные уравнения, неравенства. Способы решения

Цель занятия — овладение умениями применения способов решения показательных неравенств

Дидактическое оснащение практического занятия — методические указания по выполнению практического занятия

Время выполнения — 45 мин.

Краткие теоретические сведения

Функция у = а х = в, где а > 0, а ± 1, называется показательной. При а > 1 показательная функция является возрастающей, при 0

Основные способы решения

А) Решение неравенства вида a f ( x ) a g ( x ) , где а > 0, а ± 1 равносильно неравенству f ( x ) g ( x ), при а > 1;

3 х -2 , т.к 3>1, то у = а х возрастает на R , значит выполняется условие

Б) Решение неравенства вида a f ( x ) a g ( x ) , где а > 0, а ± 1 равносильно неравенству f ( x ) > g ( x ), при 0

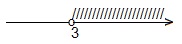
(1/2) х > (1/2) -4 , т.к 0 х убывает на R , значит выполняется условие

№ 1 Решить неравенства

№ 1 Решить неравенства

№ 2 Решить неравенство

№ 2 Решить неравенство

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 813 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 287 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 599 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1356948

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

Минпросвещения работает над единым подходом к профилактике девиантного поведения детей

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Практическая работа по математике «Решение показательных уравнений»

Практическая работа №19. Решение показательных уравнений.

рассмотреть способы решения показательных уравнений;

вырабатывать навыки решения показательных уравнений, навыки самостоятельной работы

Форма урока: урок — практикум.

Уравнение, в котором переменная содержится в показателе степени, называется показательным.

Простейшее показательное уравнение – это уравнение вида а х = b, где а>0, а 1

Уравнение = b не имеет корней, если b

При любых действительных значениях х и у справедливы равенства:

Способы решения показательных уравнений:

Вынесение общего множителя за скобки.

Введение вспомогательной переменной (замена переменной).

Разложение на множители.

Пример1 . Решить уравнения: а) 3 3 x − 3 = 27

Решение. Мы хорошо знаем, что 27 = 3 3 . Перепишем наше уравнение: 3 3 x − 3 = 3 3 . Уравнение сводится к уравнению 3 х − 3 = 3 , решив это уравнение, получим х = 2 . Ответ: х = 2 .
б) ( ) 2 x + 0 , 2 = . Решение: ( ) 2 x + 0 , 2 = ; Тогда уравнение можно переписать: ( ) 2 x + 0 , 2 = ( ; 2 х + 0 , 2 = 0 , 2 ; х = 0 . Ответ: х = 0 .
Пример 2. 2∙ — =15 (метод вынесения общего множителя за скобки)

Решение: 2∙3 х ∙3 – 3 х = 15; 3 х (2∙3- 1) = 15; 3 х ∙5= 15; 3 х = 3; х = 1

Пример 3 . – 8∙ – 9=0 ( метод введения новой переменной)

Решение: 3 2х — 8∙ — 9 =0; 3 х = t; t 2 — 8 t – 9 = 0; Д = 64 + 36 = 100; х ₁ = 9; х ₂ = -1; 3 х = 9; х=2; 3 х = -1; решений нет

Самостоятельное решение задач (практикум с элементами индивидуальной консультации)

Источник

Практическая работа по теме: «Решение показательных уравнений и неравенств»

Просмотр содержимого документа
«Практическая работа по теме: «Решение показательных уравнений и неравенств»»

Практическая работа №3

Тема: «Решение показательных уравнений и неравенств»

Цель: научиться применять свойства показательной функции для решения показательных уравнений и неравенств, закрепить знания и умения по применению методов решения показательных уравнений и неравенств для решения практических задач.

Основные теоретические положения

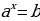
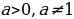
Определение. Уравнение вида , где , называется показательным.

Если

Способы решения показательных уравнений.

1. Уединить слагаемое, содержащее переменную;
2. Привести степени к одному основанию;
3. Приравнять показатели;
4. Решить полученное уравнение;
5. Записать ответ.

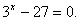
Вынесение общего множителя за скобки.

Примечание: выносим за скобки множитель с меньшим показателем.

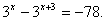
Введение новой переменной

Как правило, уравнения, решаемые этим способом, сводятся к квадратным.

Пример:

Пусть 4 x = а тогда уравнение можно записать в виде:

Сделаем обратную замену:

4 x = 4 или 4 x = 1;
х = 1 или х = 0

Ответ: х = 1 или х = 0

Определение Показательные уравнения вида 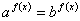называются однородными.

Суть метода: Так как показательная функция не может принимать значение, равное нулю, и обе части уравнения можно делить на одно и то же не равное нулю число, разделим обе части уравнения, например, на .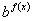

Разделим обе части уравнения на

Определение. Показательным неравенством называется неравенство, в котором переменная содержится в показателе степени.

Решение простейших показательных неравенств.

Простейшими считаются показательные неравенства вида: a x y , a x a y . (a x ≤a y , a x ≥a y ).

Так же, как и при решении простейших показательных уравнений, одинаковые основания степеней опускают, но знак нового неравенства сохраняют, если функция у=а х является возрастающей (а1); eсли же показательная функция у=а х убывает (0), то знак нового неравенства меняют на противоположный:

a x a y → x y, если a1; знак сохранен, так как функция возрастает;

a x a y → x y, если 0; функция убывает – знак поменялся;

a x a y → x y, если a1; знак сохранен, так как функция возрастает

a x a y → x y, если 0; функция убывает – знак поменялся.

Представим правую часть в виде: 0,25=( 25 /₁₀₀)=( 1 /₄)=4 -1 ;

4 5-2x -1 ; функция у=4 х с основанием 41 возрастает на R, поэтому, опуская основания степеней, знак неравенства сохраним:

Представим число 0,16 в виде степени числа 0,4. Получаем:

0,4 2х+1 ≥0,4 2 ; основание степеней – число 0,4 — удовлетворяет условию: 0; поэтому, опускаем основания степеней, а знак неравенства меняем на противоположный:

2 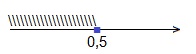х≤2-1;

1)

2)

6)

3)

4)

7)

Решите систему уравнений

5)

8)

9)

1)

2)

6)

3)

4)

7)

Решите систему уравнений

5)

8)

9)

1)

2)

6)

3)

4)

7)

Решите систему уравнений

5)

8)

9)

1)

2)

6)

3)

4)

7)

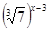
Решите систему уравнений

5)

8)

9)

Сделайте вывод по проделанной работе

От чего зависит возрастание или убывание показательной функции?

Дайте определение показательного неравенства.

Какие условия должны выполняться при решении показательных неравенств?

Источник