- Лекция 3. Биомеханический анализ движений человека
- Лекция 3
- Биомеханический анализ движений человека
- 3.1. Понятие о биомеханическом анализе
- 3.2. Механическое движение тела
- 3.3. Классификация механических характеристик движения человека
- 3.4. Кинематические характеристики движения человека или спортивных снарядов
- 3.4.1. Пространственные характеристики
- 3.4.2. Временные характеристики
- 3.4.3. Пространственно-временные характеристики
- ТЕМА: Определение момента инерции тела спортсмена
- Лабораторная работа: Определение момента инерции твёрдых тел 2
Лекция 3. Биомеханический анализ движений человека
В третьей лекции по дисциплине «Биомеханика двигательной деятельности» описан биомеханический анализ движений человека Биомеханический анализ движений человека начинается с регистрации и определения различных механических характеристик движущегося или покоящегося тела: кинематических, динамических, энергетических и др. Некоторые из этих характеристик определяются экспериментально, а остальные – расчетным путем.
Лекция 3
Биомеханический анализ движений человека
3.1. Понятие о биомеханическом анализе
Биомеханический анализ движений человека всегда начинается с определения различных характеристик движущегося тела. Этими характеристиками могут быть различные механические характеристики (например, перемещение, скорость, ускорение) и биологические характеристики (сила тяги мышцы, время суммарной электрической активности мышцы). Некоторые из этих характеристик определяются экспериментально, а остальные – расчетным путем. В биомеханике широко используются механические характеристики движущегося тела. Прежде чем перейти к описанию механических характеристик введем ряд понятий, характеризующих механическое движение тел.
3.2. Механическое движение тела
Механическое движение тела – это изменение положения тела в пространстве относительно других тел. Механическое движение является неотъемлемым компонентом функционирования человеческого организма. Чтобы определить положение какого-либо тела в пространстве, прежде всего, нужно выбрать тело отсчета.
Тело отсчета – тело, которое условно считается неподвижным и относительно которого рассматривается движение данного тела.
Выбор тела отсчета определяется соображениями удобства для изучения данного движения. Обычно за тело отсчета принимается тело, неподвижное относительно поверхности Земли.
Система отсчета состоит из тела отсчета, системы координат и часов, синхронно идущих во всех точках пространства.
Физические величины бывают скалярными и векторными.
Векторная величина отображается отрезком прямой со стрелкой на одном конце. Длина отрезка в выбранном масштабе выражает числовое значение векторной величины, а стрелка указывает ее направление. Векторную величину обозначают буквой с черточкой над ней (или стрелкой) или жирным шрифтом. В настоящей лекции векторные величины будут обозначаться жирным шрифтом.
Скалярная величина (от лат. scalaris — ступенчатый) в механике – величина, каждое значение которой может быть выражено одним числом. То есть скалярная величина определяется только своим значением, в отличие от векторной, которая кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д.
Тело человека – это не материальная точка, а очень сложная биомеханическая система переменной конфигурации. При изучении кинематики движений человека мы можем исследовать движение отдельных точек его тела (например, центров суставов) и производить анализ и оценку их движений с помощью механических характеристик. При изучении движений отдельных звеньев тела человека мы можем вычленить и наблюдать наиболее простые формы движения тела – поступательное и вращательное.
Поступательным движением тела называется такое движение, при котором всякая прямая, проведенная в этом теле, перемещается, оставаясь параллельной самой себе. Поступательное движение не следует смешивать с прямолинейным. При поступательном движении тела траектории его точек могут быть как прямолинейными, так и криволинейными (например, траектория полета ядра или траектория ОЦТ тела человека в полетной фазе бегового шага).
При поступательном движении тела все его точки движутся по одинаковым и параллельно расположенным траекториям и имеют в каждый момент времени равные скорости и равные ускорения. Поэтому поступательное движение тела вполне определяется движением какой-либо его одной точки, а, значит, задача изучения поступательного движения тела сводится к изучению движения любой его точки.
Вращательным движением тела называется такое движение, при котором какие-либо две его точки остаются все время неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Траекторией движения любой точки тела при вращательном движении будет окружность.
3.3. Классификация механических характеристик движения человека
Исследуя движения человека, измеряют количественные показатели механического состояния тела человека или его движения, а также движения звеньев тела, то есть регистрируют механические характеристики движения.
Механические характеристики движения человека – это показатели и соотношения, используемые для количественного описания и анализа двигательной деятельности человека.
Механические характеристики делятся на две группы:
- кинематические (описывают внешнюю картину движений);
- динамические (несут информацию о причинах возникновения и изменения движения человека, а также показывают, как меняются виды энергии при движениях и происходит сам процесс изменения энергии).
3.4. Кинематические характеристики движения человека или спортивных снарядов
Кинематические характеристики движения человека делятся на следующие группы:
3.4.1. Пространственные характеристики
Для простоты, будем считать, что тело человека является твердым телом. Тогда положение тела в пространстве будут характеризовать следующие пространственные характеристики:
Координаты тела – это пространственная мера местоположения тела относительно системы отсчета.
Положение тела в пространстве может быть описано с помощью декартовых и полярных координат. Для определения положения точки на плоскости в декартовой системе координат достаточно двух линейных координат: x и y, в пространстве – трех: x, y, z.
Перемещение тела (ΔS) – вектор, соединяющий начальное положение точки (тела) с его конечным положением. При прямолинейном движении перемещение тела совпадает с траекторией движущегося тела. При криволинейном – не совпадает.
А.В.Самсоновой с соавт. (2016) изучалось влияние «моста» на характеристики движения штанги. Авторами установлено, что «сведение лопаток» позволяет уменьшить значение модуля перемещения штанги из положения «штанга на вытянутых руках» в положение «штанга на груди» на 2,5 см, а «мост» — на 6,7 см. Применение технических приемов позволяет уменьшить механическую работу по подъему штанги массой 144 кг на 43,7 Дж и 88,8 Дж соответственно (рис.3.1)
Рис.3.1. Перемещение штанги из положения «штанга на вытянутых руках» в положение «штанга на груди» (А.В.Самсонова с соавт., 2016)
Траектория движения тела – это геометрическое место положений движущегося тела в рассматриваемой системе координат.
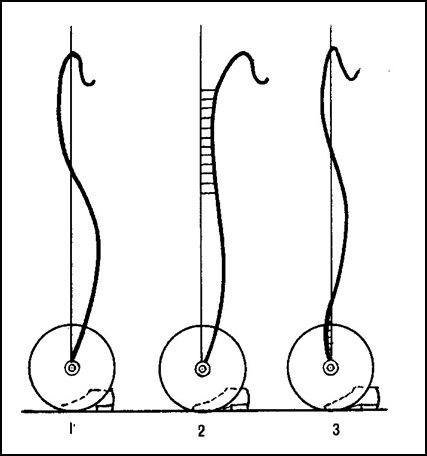
В тяжелой атлетике одним из критериев мастерства является траектория движения штанги. На рис.3.2 представлены различные варианты траектории штанги. Считается, что ширина «коридора» в котором заключена траектория движения штанги не должна превышать 12 см.
Рис.3.2. Оптимальная (1) и нерациональные (2 и 3) траектории движения штанги при выполнении тяжелоатлетических упражнений.
Путь – физическая величина (скалярная), численно равная длине траектории движения точки или тела.
3.4.2. Временные характеристики
Временные характеристики раскрывают движение во времени. К временным характеристикам относятся:
Длительность движения тела – это временная мера, которая измеряется разностью моментов времени окончания и начала движения тела.
Фаза – это часть движения, в течение которой решается самостоятельная двигательная задача.
Например, в беге существуют фаза опоры и фаза полета. Каждая из этих фаз характеризуется определенной длительностью.
Темп движений определяется количеством движений звена человека (например руки или ноги) в единицу времени. Эта характеристика определяется для повторных (циклических движений). Темп движений – величина, обратная длительности движений. Чем больше длительность движений, тем ниже темп. При педалировании в максимальном темпе спортсмен выполняет три цикла в секунду, при беге – 2,8 циклов в секунду, при беге на коньках – 1,8 циклов в секунду.
В атлетизме темп выполнения силовых упражнений существенно влияет на гипертрофию скелетных мышц. Установлено, что эксцентрические упражнения, выполняемые в высоком темпе, оказывают большее повреждающее действие на скелетные мышцы по сравнению с умеренным темпом. Вследствие этого степень гипертрофии мышц при выполнении силовых упражнений в высоком темпе будет больше.
Ритм движений – временная мера соотношения частей (фаз) движения.
Пример. В беге отношение фазы опоры к фазе полета характеризует ритм движений бегуна. Это отношение называется ритмическим коэффициентом. У детей 5-6 лет ритмический коэффициент равен двум, то есть фаза опоры значительно превышает фазу полета. У взрослых мужчин 20-29 лет этот значение ритмического коэффициента равно 1,4. У сильнейших спринтеров этот показатель равен 0,8.
Во многих видах спорта, например, толкании ядра, барьерном беге ритм является важнейшим критерием технического мастерства спортсмена.
3.4.3. Пространственно-временные характеристики
К пространственно-временным характеристикам относят:
Поступательное движение тела
Скорость тела (V) – это векторная величина, определяющая быстроту и направление изменения положения тела в пространстве с течением времени. Скорость измеряется отношением перемещения тела (ΔS) к затраченному времени V= ΔS/Δt.
В спорте скорость движения человека или снаряда является критерием спортивного мастерства. Существует ряд видов спорта, в которых чем выше скорость перемещения спортсмена, тем выше результат, табл. 3.1.
Источник
ТЕМА: Определение момента инерции тела спортсмена



ЛАБОРАТОРНАЯ РАБОТА № 5
Цель: освоить методику определения инерционности тела на опоре по показателям момента инерции.
Момент инерции — это мера, характеризующая степень инертности тела при вращательных движениях, т.е. способности тела сохранять свое состояние покоя или равномерного вращательного движения. Момент инерции равен сумме произведений масс материальных точек тела на квадрат расстояния от соответствующих точек до оси вращения:
где: JС — момент инерции тела спортсмена относительно точки С, кг.м 2 ;
ri — расстояние от центра масс i-го звена до точки С, м.
1. Записать абсолютные массы звеньев тела (кг) в таблицу 1. Сумма всех абсолютных масс звеньев тела равна массе тела М.
2. Измерить расстояние от центра масс каждого звена до ОЦМ тела (мм), и записать полученные данные в соответствии с масштабом в таблицу 1.
3. Вычислить квадрат расстояний от центра масс каждого звена до левого ОЦМ тела. Полученные данные занести в таблицу 1.
4. Вычислить моменты инерции каждого звена тела спортсмена относительно ОЦМ по формуле:
5. Вычислить момент инерции тела спортсмена JС относительно ОЦМ, просуммировав моменты инерции всех звеньев.

6. При выведении из равновесия (опрокидывании) центром вращения тела является одна из крайних точек опоры тела в данной статической позе. Вычислить момент инерции JA тела спортсмена относительно левой и правой точек опоры тела по формуле:


где 

7. Оценить инерционность тела, сравнив моменты инерции тела относительно крайних точек опоры тела (левой и правой) и сделать выводы.
Источник
Лабораторная работа: Определение момента инерции твёрдых тел 2
| Название: Определение момента инерции твёрдых тел 2 Раздел: Рефераты по физике Тип: лабораторная работа Добавлен 22:08:29 22 июня 2011 Похожие работы Просмотров: 4016 Комментариев: 21 Оценило: 3 человек Средний балл: 5 Оценка: неизвестно Скачать | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Для экспериментальной проверки теоремы Штейнера и определения момента инерции в данной работе используется стандартная установка универсального маятника ФПМО — 4. Это настольный прибор (рис. 4.1), на вертикальной стойке основания 1 которого крепится кронштейн 2, который имеет возможность поворота вокруг стойки на 360° и фиксация в любом выбранном положении. С одной стороны кронштейна 2 подвешен математический маятник, а с другой — физический. Математический маятник представляет собой металлический шарик 3 на бифилярном подвесе 4. Физический маятник — стальной стержень 5, подвешенный на опорной призме 6. Опорная призма 6 может перемещаться по всей длине стержня и фиксироваться в требуемом положении. Стержень 5 имеет кольцевые проточки, которые служат для надежной фиксации опорных призм. Установка снабжена фотоэлектрическим датчиком 7, который закреплен на вертикальной стойке с помощью кронштейна 8 и имеет возможность перемещаться как вдоль, так и вокруг стойки и фиксироваться в любом положении. Датчик предназначен для выдачи сигналов на Миллисекундомер 9. Физический Миллисекундомер выполнен самостоятельным прибором с цифровой индикацией времени и количества полных периодов колебаний маятника. 3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ Средняя величина периода колебаний маятника: t — продолжительность колебаний; n — число колебаний за время t . Формула для экспериментального расчета момента инерции прямого тонкого стержня:
T — период колебаний маятника; l — расстояние от центра масс до точки подвеса маятника; m — Масса маятника; g — Ускорение свободного падения. Истинное значение величины t лежит в интервале tизм — s (t) ≤ t ≤ t изм + s (t) , где tизм – значение величины t , полученное при измерении, а величина s (t) – абсолютная погрешность измерения величины t . Это неравенство принято записывать в следующем виде. s сис (t) – систематическая абсолютная погрешность. Мерой точности результатов измерений является относительная погрешность. Формула для расчета погрешности косвенных измерений: Класс точности прибора не указан, выбираем значение абсолютной погрешности ∆ l как половину цены деления (0,005 м). Формула для теоретического расчета момента инерции прямого тонкого стержня длиной d и массой m относительно оси, перпендикулярной к стержню и проходящей через его середину: Выражение теоремы Штейнера: где, I0 –момент инерции относительно оси, проходящий через центр масс; l – расстояние между осями. Доверительный интервал для l 2 : 4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ. Результаты прямых и косвенных измерений представлены в таблице.
На основании полученных опытных данных рассчитаем среднюю величину периода колебаний маятника по формуле (3.1) и результаты занесём в таблицу 1. Исходя из опытных данных таблицы 1, зная массу маятника m и расстояние от центра масс до точки подвеса маятника l , вычислим по формуле (3.2) значение момента инерции маятника I . Рассчитаем относительные погрешности оценки точности измерений, учитывая абсолютную погрешность замера времени колебаний σ( t ) = ±2мс, относительную погрешность определения массы δ( m ) =2% по формулам (3.3) — (3.13): Рассчитаем относительную погрешность момента инерции по формуле (3.4) Рассчитаем доверительный интервал σ( I ) для каждого значения момента инерции I по формуле (3.9) и результаты занесем в таблицу 2. Определим t , l 2 , I с учетом доверительных интервалов и результаты занесем в таблицу 2 для каждого значения. Таблица доверительных интервалов.
На основании полученных опытных и расчётных данных построим график зависимости момента инерции твёрдого тела I от квадрата расстояния l 2 , от оси вращения до центра масс. Проведём через экспериментальные точки и доверительные интервалы прямую линию, экспериментальной зависимости I = f (l 2 ). Используя полученные данные, построим линеаризованный график этой зависимости в координатах I , l 2 , с учетом доверительных интервалов: Рассчитаем коэффициенты a и b линеаризованного графика методом наименьших квадратов:
S1 = S2 = S3 = S4 = S5 S6 = Используя график линеаризованной зависимости I = f (l 2 ), изображённой на рис.4.1 определим собственный момент инерции I 0 относительно оси проходящей через его центр масс, что составило: Произведём расчёт момента инерции прямого тонкого стержня длиной d относительно оси перпендикулярной стержню и проходящей через его середину по формуле (3.11): Экспериментальное значение массы стержня определяем по коэффициенту наклона прямой, m=(0,0340 кг×м 2 – 0,0144 кг×м 2 )/(0,0625 м 2 – 0,0081м 2 )=0,0196 кг×м 2 /0,0544 м 2 =0,360 кг. Анализ графика на рис.4.1. показывает, что через экспериментальные точки и доверительные интервалы можно провести прямую линию. Следовательно, зависимость I = f (l 2 ) является линейной, значит, зависимость момента инерции твёрдого тела от квадрата расстояния от оси вращения до центра масс подтверждена экспериментально. Найденное значение момента инерции I 0 прямого тонкого стержня длиной d на графике и рассчитанное по формуле (3.11) совпадают.
В результате проделанной лабораторной работы мы определили момент инерции I 0 физического маятника относительно оси, проходящей через центр масс, и момент инерции относительно оси, не проходящий через центр его масс и проверили справедливость теоремы Штейнера на примере физического маятника. 6. Контрольные вопросы. 6.1 Как формулируется понятия инерции материальной точки и твёрдого тела? Внутреннее свойство тел сохранять состояние своего движения в отсутствии сил и реагировать на их действия изменением состояния движения, сопротивляясь этим изменениям, называют, в общем случае, инерционностью. Количественной мерой воздействия на тело в каждый момент времени, изменяющего состояние его поступательного движения, является сила F . Равенство силы нулю означает неизменность состояния тела – движения или покоя. Протяженное во времени воздействие оценивается как произведение силы на время её действия F∆ t , называют эту меру действия импульсом силы. Импульс силы и сила – причинные динамические характеристики по отношению к объекту их приложения. Импульс переменной во времени силы, приходящийся на бесконечно малый интервал времени dt , есть дифференциал импульса силы Fdt . Равенство нулю дифференциала предполагает постоянство импульса тела: при неизменной массе тела вектор скорости его поступательного движения и сонаправленный с ним вектор импульса будут оставаться неизменными по величине и направлению (F = 0, mv = const ). История формирования понятий динамики твёрдого тела такова, что между характеристиками поступательного движения материальной точки и вращательного движения твёрдого тела имеет место определённая аналогия, вытекающая из общности материалистических представлений о причинах и следствиях. Так, центральное понятие динамики материальной точки действие (воздействие, взаимодействие), описываемое силой F и импульсом силы F∆ t , в динамике твёрдого тела дополнилось характеристиками: моментом силы M – мерой мгновенного (текущего) действия – и импульсом момента силы M∆ t – мерой протяжённого во времени действия. Момент силы, или вращательный момент, определяется как векторное произведение действующей на тело силы и радиус-вектора точки приложения этой силы относительно какой-либо выбранной (выделенной) точки: M = r * F, M = r * F * sin ( r , F ). Действуя на тело продолжительное время, вращательный момент обуславливает изменение состояния движения тела. По аналогии с теорией движения материальной точки, в которой импульс силы, как причинный фактор, обуславливает следствие – приращения импульса тела, равное импульсу силы, — в динамике твёрдого тела импульс момента силы вызывает изменение момента импульса тела L (M * dt = dL ). 6.2 В каких ситуациях применима теорема Штейнера? Если известен момент инерции тела относительно любой оси, проходящей через центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера. Суть, которой состоит в применении формулы: где l – расстояние между осью симметрии тела и осью вращения, I 0 – момент инерции тела относительно оси симметрии. Момент инерции I относительно произвольной оси равен сумме момента инерции I 0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями: 6.4 Под действием какой силы совершается колебательное движение маятника? Колебательные движения физического маятника совершаются под действием силы тяжести около неподвижной горизонтальной оси, не проходящей через его центр тяжести. Силу тяжести P = mg можно разложить на две составляющие, одна из которых P 2 уравновешивается реакцией подвеса. Под действием другой P1 маятник приходит в движение. На основании второго закона Ньютона для динамики вращательного движения запишем: где M – момент вращающей силы; ε – угловое ускорение. Модуль составляющей силы P1 = P sin φ . Знак «минус» выбран потому, что действующая сила направлена в сторону, противоположную положительному направлению отклонения маятника. 6.5 Является ли момент инерции аддитивной величиной? Момент импульса твёрдого тела складывается из моментов импульса составляющих его материальных точек, т.е. момент импульса – аддитивная величина. Момент импульса материальной точки относительно произвольной точки пространства называют векторное произведение радиус-вектора материальной точки в системе отсчёта выбранной точки: 6.6 Объяснить метод определения момента инерции с помощью физического маятника. В основе определения момента инерции тел с помощью физического маятника лежит экспериментальная проверка справедливости теоремы Штейнера. Зная ускорение свободного падения g , массу m , экспериментально измерив длину l и определив период T можно вычислить момент инерции маятника. Зависимость I = f ( l ) , как следует из выражения I = I 0 + ml 2 нелинейная и график зависимости представляет собой возрастающую кривую, по виду которой нельзя утверждать о проверяемой зависимости. Единственным графиком по виду, которого можно однозначно судить о характере исследуемой зависимости, является прямая линия, поэтому используем метод линеаризации. В данном случае такими переменными являются I и l 2 , следовательно, для проверки построим график I = f ( l 2 ) , при этом на него нанесём экспериментальные точки и доверительные интервалы. Через экспериментальные точки и доверительные интервалы (рис. 4.1) проводим прямую линию, т.е. экспериментальная зависимость [I = f ( l 2 ) ] момента инерции твёрдого тела от квадрата расстояния от оси вращения до центра масс является линейной, значит, правильность соотношения I = I 0 + ml 2 подтверждена экспериментально. Используя график линеаризованной зависимости I = f ( l 2 ) можно вычислить массу стержня и собственный момент инерции, а также сравнить результаты расчёта и опыта. Для этого сравним наше уравнение с уравнением прямой где а – угловой коэффициент, b – отрезок, отсекаемый прямой на оси y . Угловой коэффициент определяется как где ∆ x – приращение аргумента, ∆ y – соответствующее приращение функции. 6.7 Какой маятник называется физическим? Физическим маятником называется любое твёрдое тело, которое под действием силы тяжести совершает колебания около неподвижной горизонтальной оси, не проходящей через центр масс. Период Т малых колебаний физического маятника равен: где I – момент инерции маятника относительно оси О , m – масса маятника, l – расстояние от точки A до оси О . 6.8 При каких формальных допущениях справедлива формула периода колебаний маятника (3.7)? Собственные механические колебания возникают в физическом маятнике под действием силы тяжести вокруг неподвижной оси. Эти колебания в первом приближении не подвержены воздействию внешних сил. Модуль составляющей силы тяжести твёрдого тела определяется как P 1 = P * sin φ . При малых углах отклонения sinφ ≈ φ, а период колебаний не зависит от амплитуды колебаний. Поэтому формула периода колебания маятникаT = 2π ( I /( mgl )) 1/2 справедлива в случаях, когда угол отклонения маятника в положении равновесия мал и не должен превышать 5-10°. 6.9 Как записывается основной закон динамики вращательного движения? Основное уравнение (закон) динамики вращательного движения: при воздействии момента внешних сил твёрдое тело вращается вокруг неподвижной оси с угловым ускорением, прямо пропорциональным моменту сил и обратно пропорциональным моменту инерции тела относительно данной оси: где М – результирующий момент внешних сил, действующих на тело, ß – угловое ускорение, I – момент инерции тела относительно оси вращения. Источник |






 , (3.2)
, (3.2)
 ; S1 =0.2471
; S1 =0.2471  ; S2 = 0,1695
; S2 = 0,1695  ; S3 = 0,007923;
; S3 = 0,007923;  ; S4 = 0,01412;
; S4 = 0,01412;  ; S5 = 0.037757;
; S5 = 0.037757;  ; S6 =0,0048;
; S6 =0,0048; 



