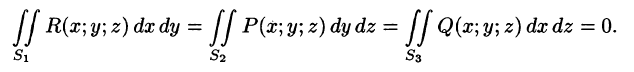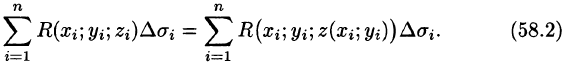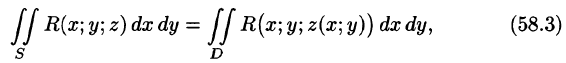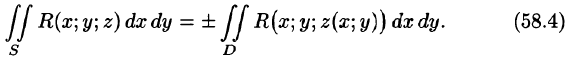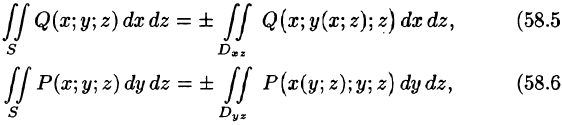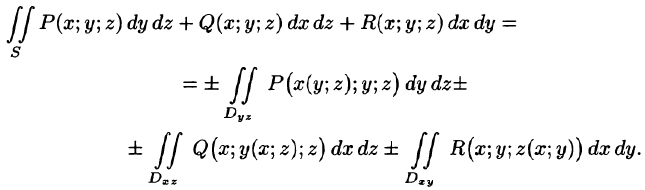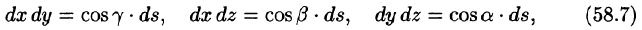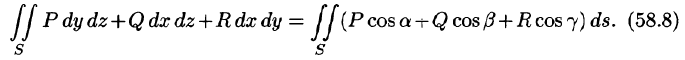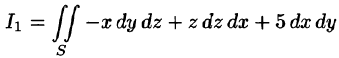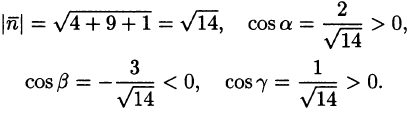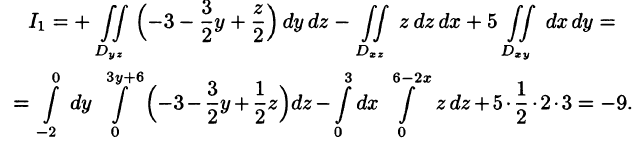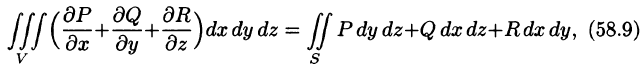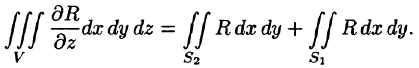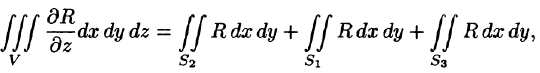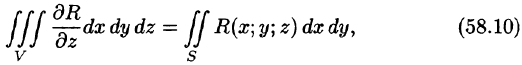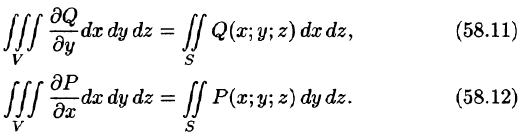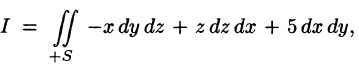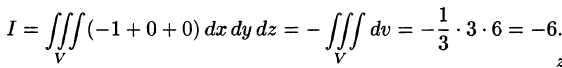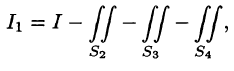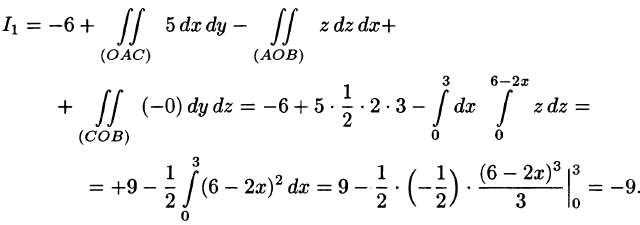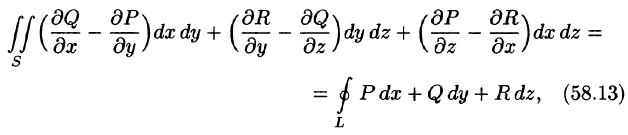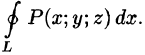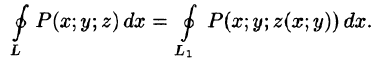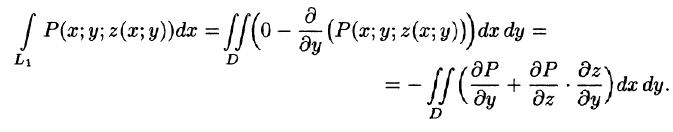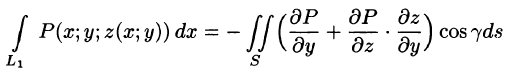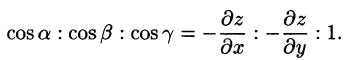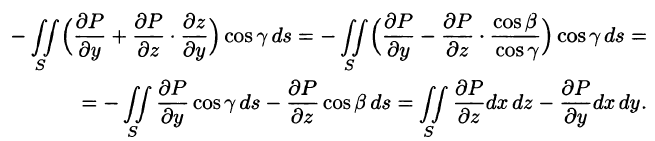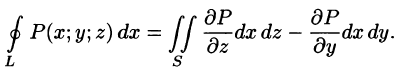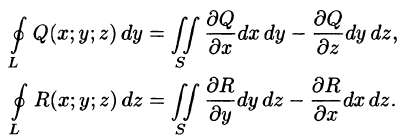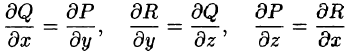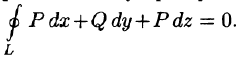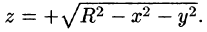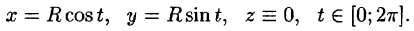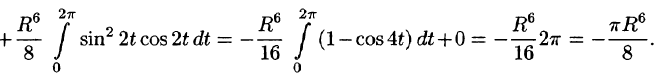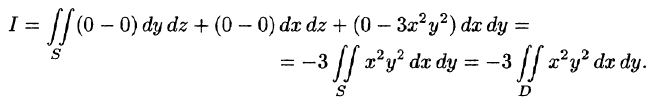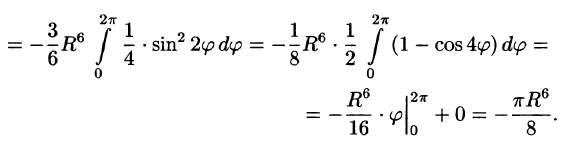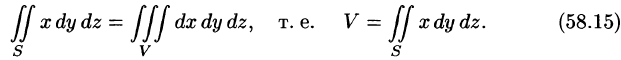- Поверхностный интеграл первого рода и его свойства
- Поверхностный интеграл первого рода < по площади поверхности >и его свойства
- Далее:
- Поверхностные интегралы в математике с примерами решения и образцами выполнения
- Поверхностный интеграл первого рода
- Интеграл по цилиндрической поверхности
- Интеграл по сферической поверхности
- Определение и свойства поверхностных интегралов
- Поверхностный интеграл I рода
- Вычисление поверхностного интеграла I рода
- Некоторые приложения поверхностного интеграла I рода
- Площадь поверхности
- Масса поверхности
- Моменты, центр тяжести поверхности
- Поверхностный интеграл II рода
- Вычисление поверхностного интеграла II рода
- Формула Остроградского-Гаусса
- Формула Стокса
- Некоторые приложения поверхностного интеграла II рода
Поверхностный интеграл первого рода и его свойства
Поверхностный интеграл первого рода и его свойства
- Услуги проектирования
- Поверхностный интеграл
- Поверхностный интеграл первого рода и его свойства
Поверхностный интеграл первого рода < по площади поверхности >и его свойства
Определение поверхностного интеграла первого рода
Пусть в пространстве переменных $\mathbf < \textit < x,y,z >> \mathbf < >$ задана кусочно-гладкая поверхность $\sigma $, на которой определена функция $\mathbf < \textit < f >> (\mathbf < \textit < x >> $,$\mathbf < \textit < y >> $,$\mathbf < \textit < z >> )$.$\mathbf < >$
Разобьём поверхность на $n$ частей $\sigma _1 ,\sigma _2 ,\ldots \sigma _i ,\ldots \sigma _n $, на каждой из частей $\sigma _i $ выберем произвольную точку $M_i (x_i ,y_i ,z_i )$, найдём $f(M_i )=f(x_i ,y_i ,z_i )$ и площадь части $\sigma _i $ < которую будем обозначать тем же символом $\sigma _i )$ и составим интегральную сумму $\sum\limits_ < i=1 >^n < f(M_i )\cdot \sigma _i >$.
Если существует предел последовательности интегральных сумм при $\mathop < \max >\limits_ < i=1,2,\ldots n >diam\sigma _i \to 0$, не зависящий ни от способа разбиения поверхности $\sigma $ на части $\sigma _i (i=1,2,\ldots ,n)$, ни от выбора точек $M_i $, то функция $\mathbf < \textit < f >> (\mathbf < \textit < x >> $,$\mathbf < \textit < y >> $,$\mathbf < \textit < z >> )$ называется интегрируемой по поверхности $\sigma $, а значение этого предела называется поверхностным интегралом первого рода, или поверхностным интегралом по площади поверхности и обозначается $\iint\limits_\sigma < f(M)\cdot d\sigma >$.
Теорема существования Если функция $\mathbf < \textit < f >> (\mathbf < \textit < x >> $,$\mathbf < \textit < y >> $,$\mathbf < \textit < z >> )$ непрерывна на поверхности $\sigma $, то она интегрируема по этой поверхности.
Свойства поверхностного интеграла первого рода
Аналогичны по формулировке и доказательству свойствам рассмотренных ранее интегралов первого рода.
- Линейность. $\iint\limits_\sigma < (\lambda \,f+ >\mu \,g)d\sigma =\lambda \iint\limits_\sigma < fd\sigma >+\mu \iint\limits_\sigma < gd\sigma >$
- Аддитивность $\iint\limits_ < \sigma _1 \cup \sigma _2 >< fd\sigma >=\iint\limits_ < \sigma _1 >< fd\sigma >\iint\limits_ < \sigma _2 >< fd\sigma >$
- $\iint\limits_\sigma < d\sigma >=S_\sigma -$ площадь поверхности.
- Если $f(x,\,y,\,z)\geqslant g(x,\,y,\,z)$, то $\iint\limits_\sigma < fd\sigma \geqslant \iint\limits_\sigma < gd\sigma >> $ < если $f\geqslant 0$, то $\iint\limits_\sigma < fd\sigma >\geqslant 0)$,
- Теорема об оценке Если $m\leqslant f\left( < x,\,y,\,z >\right)\leqslant M$, то $mS_\sigma \leqslant \iint\limits_\sigma < fd\sigma >\leqslant MS_\sigma $,
- Теорема о среднем Пусть функция $f(M)=f(x,\,y,\,z)$ непрерывна на кусочно-гладкой ограниченной поверхности $\sigma $. Тогда на поверхности найдется точка С, такая что $f(C)=\frac < 1 >< S_\sigma >\iint\limits_\sigma < f\left( < x,\,y,\,z >\right)d\sigma > $
Доказательство
Первые четыре свойства доказываются аналогично подобным свойствам в двойном, тройном интегралах, криволинейном интеграле первого рода < записью соотношений в интегральных суммах и предельным переходом >. Во втором свойстве используется возможность такого разбиения поверхности на две части, чтобы ни один элемент разбиения не содержал граничные точки этих частей в качестве своих внутренних точек.
Теорема об оценке следует из свойств 3, 4.
Теорема о среднем, как и ранее, использует теоремы Вейерштрасса и Больцано-Коши для функций, непрерывных на замкнутых ограниченных множествах.
Седьмое, персональное, свойство — независимость поверхностного интеграла первого рода от выбора стороны поверхности
Далее:
Соленоидальное векторное поле
Функции 2-значной логики. Лемма о числе функций. Элементарные функции 1-ой и 2-х переменных
Свойства тройного интеграла
Полином Жегалкина. Теорема о представлении в виде полинома Жегалкина
Теорема об алгоритме распознавания полноты
Вычисление поверхностного интеграла второго рода
Замыкание. Свойства замыкания. Теорема о сведении к заведомо полной системе
Критерий полноты <формулировка>. Лемма о несамодвойственной функции
Вычисление тройного интеграла. Теорема о переходе от тройного интеграла к повторному
Вычисление криволинейного интеграла первого рода. Примеры
Формулы. Равенство функций и эквивалентность формул. Основные эквивалентности
Свойства криволинейного интеграла второго рода
Критерий полноты <формулировка>. Лемма о немонотонной функции
СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице
Огравление $\Rightarrow $
Источник
Поверхностные интегралы в математике с примерами решения и образцами выполнения
При изучении темы «Поверхностные интегралы» вы познакомитесь с понятием интеграла по поверхности от функции трех
переменных и научитесь сводить его к двойному (а затем — к повторному), проецируя заданную поверхность на одну из координатных плоскостей. Кроме того, вы научитесь вычислять интегралы по части цилиндрической и сферической поверхностей.
Поверхностный интеграл первого рода
Постановка задачи. Вычислить поверхностный интеграл
где 
и некоторыми неравенствами.
План решения. Поверхностный интеграл сводится к двойному
проецированием 
где D — проекция 
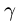
к поверхности 
Замечание:
Если уравнение F(x,y,z) = 0 не определяет однозначно функцию z = z(x,y), то проецируем 
также разбить поверхность на части и воспользоваться аддитивностью интеграла).
1.Единичные нормальные векторы 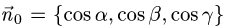
2.Проекцию D поверхности 

3.Находим z = z(x, у), решая уравнение F(x, у, z) = 0.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному.
Пример:
Вычислить поверхностный интеграл
где 
расположенная в первом октанте (т.е. 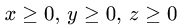
Решение:
1.Единичные нормальные векторы 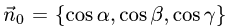
поверхности, заданной уравнением F(x, у, z) = 0, определяются формулой
В данном случае F(x,y,z) = х + 2у + 3z — 1. Следовательно,
2.Поверхность 
Ее проекцию D на плоскость XOY находим, исключая z из условий,
определяющих 
3.Из уравнения х + 2у + 3z — 1 = 0 находим z(x, у) = (1 — х — 2у)/3.
4.Переходим от поверхностного интеграла к двойному по формуле (1) и вычисляем двойной интеграл, сводя его к повторному:
Ответ.
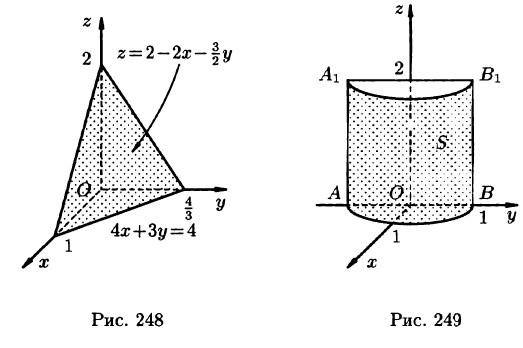
Интеграл по цилиндрической поверхности
Постановка задачи. Вычислить поверхностный интеграл
где 
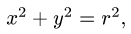
z = 0 и z = h.
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
В этих координатах поверхность задается условиями
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
где 
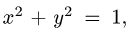
z = 0, z = 2.
Решение:
1.Вводим на заданной поверхности (цилиндре) криволинейные
координаты
В этих координатах поверхность задается условиями
2.Так как 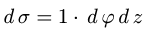
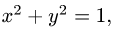
3.Вычисляем повторный интеграл:
Ответ.
Интеграл по сферической поверхности
Постановка задачи. Вычислить поверхностный интеграл
где 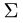
1.Вводим на заданной поверхности (сфере) криволинейные координаты
В этих координатах поверхность задается условиями
2.Так как 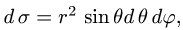
3.Вычисляем повторный интеграл и записываем ответ.
Пример:
Вычислить поверхностный интеграл
где 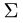
Решение:
1.Вводим на заданной поверхности (сфере) криволинейные координаты
В этих координатах поверхность задается условиями
2.Так как 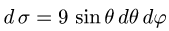
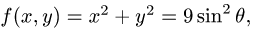
3.Вычисляем повторный интеграл:
Ответ.
Определение и свойства поверхностных интегралов




Поверхностный интеграл I рода
Обобщением двойного интеграла является так называемый поверхностный интеграл.
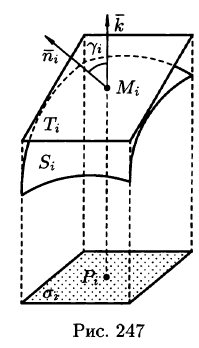
Пусть в точках некоторой поверхности S, с площадью S , пространства Oxyz определена непрерывная функция f(х; у; z). Разобьем поверхность S на п частей 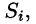
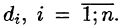
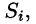
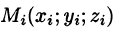
Она называется интегральной для функции f(x;y;z) по поверхности S.
Если при 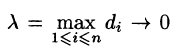
Таким образом, по определению,
Отметим, что «если поверхность S гладкая (в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки по поверхности), а функция f(x;y;z) непрерывна на этой поверхности, то поверхностный интеграл существует» (теорема существования).
Поверхностный интеграл I рода обладает следующими свойствами:
3. Если поверхность S разбить на части 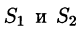
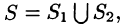
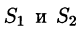
4.Если на поверхности S выполнено неравенство
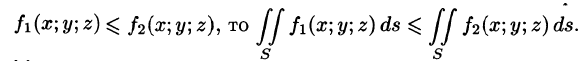
7.Если f(x; у, z) непрерывна на поверхности S, то на этой поверхности существует точка 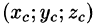
(теорема о среднем значении).
Вычисление поверхностного интеграла I рода
Вычисление поверхностного интеграла I рода сводится к вычислению двойного интеграла по области D — проекции поверхности S на плоскость Оху.
Разобьем поверхность S на части 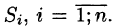
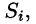
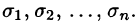
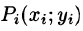
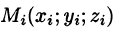

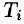
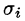
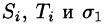
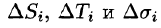

Обозначив через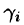
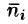
(область 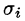
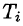
Если поверхность S задана уравнением z = = z(x;y), то, как известно (см. (45.2)), уравнение касательной плоскости в точке 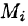
где 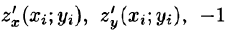
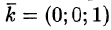
Равенство (57.4) принимает вид
В правой части формулы (57.2) заменим 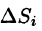
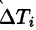
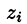
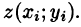

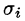
выражающую интеграл по поверхности S через двойной интеграл по проекции S на плоскость Оху.
Отметим, что если поверхность S задана уравнением вида у = y(x;z) или х = x(y;z), то аналогично получим:
где 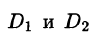
Пример:
Вычислить 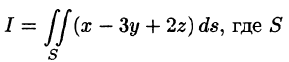
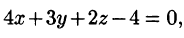
Решение:
Запишем уравнение плоскости в виде
Находим 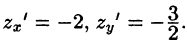
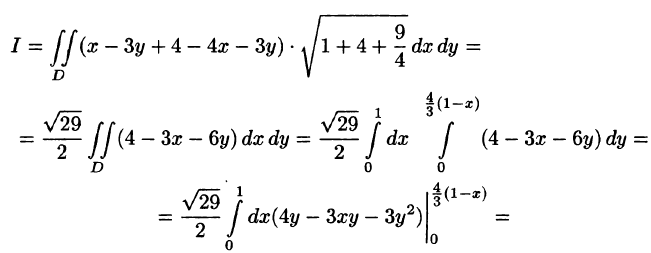
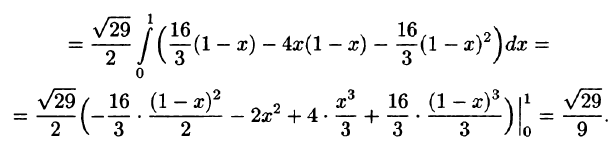
Пример:
где S — часть цилиндрической поверхности 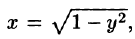
Решение:
Воспользуемся формулой (57.6). Поскольку
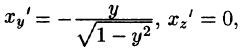
то где 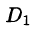
Некоторые приложения поверхностного интеграла I рода
Приведем некоторые примеры применения поверхностного интеграла I рода.
Площадь поверхности
Если поверхность S задана уравнением z = z(x; у), а ее проекция на плоскость Оху есть область D, в которой z(x;y), zx'(x; у) и zy'(x;y) — непрерывные функции, то ее площадь S вычисляется по формуле
Кроме того, поверхностный интеграл применяют для вычисления массы, координат центра масс, моментов инерции материальных поверхностей с известной поверхностной плотностью распределения массы 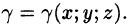
Масса поверхности
Пусть плотность распределения массы материальной поверхности есть 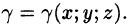
- Разбиваем поверхность S на п частей
площадь которой обозначим
.
- Берем произвольную точку
в каждой области
. Предполагаем, что в пределах области
плотность постоянна и равна значению ее в точке
.
- Масса
области
мало отличается от массы
фиктивной однородной области с постоянной плотностью
4. Суммируя 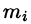
5.За точное значение массы материальной поверхности S принимается предел, к которому стремится полученное приближенное значение при стремлении к нулю диаметров областей 
Моменты, центр тяжести поверхности
Статистические моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по соответствующим формулам:
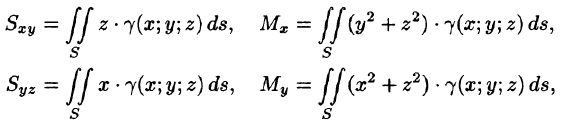
Пример:
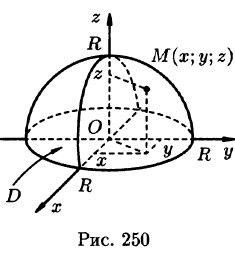
Найти массу полусферы радиуса R, если в каждой точке поверхности плотность численно равна расстоянию этой точки от радиуса, перпендикулярного основанию полусферы. Решение: На рисунке 250 изображена полусфера радиуса R. Ее уравнение 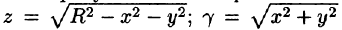
По формуле (57.7) находим:
Переходим к полярным координатам:
внутренний интеграл вычислен с помощью подстановки r= Rsint:
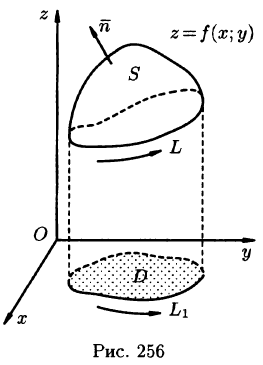
Поверхностный интеграл II рода
Поверхностный интеграл II рода строится по образцу криволинейного интеграла II рода, где направленную кривую разлагали на элементы и проектировали их на координатные оси; знак брали в зависимости от того, совпадало ли ее направление с направлением оси или нет.
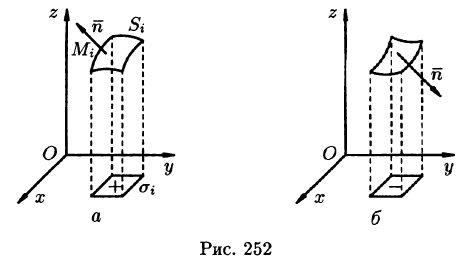
Пусть задана двусторонняя поверхность (таковой является плоскость, эллипсоид, любая поверхность, задаваемая уравнением z =f(x;y), где f(x;y), 
Далее, пусть в точках рассматриваемой двусторонней поверхности S в пространстве Oxyz определена непрерывная функция f(x; у; z). Выбранную сторону поверхности (в таком случае говорят, что поверхность ориентирована) разбиваем на части 
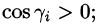
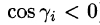
где 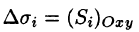

Предел интегральной суммы (58.1) при 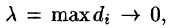

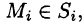
Аналогично определяются поверхностные интегралы II рода по переменным у и z и z и х:
Общим видом поверхностного интеграла II рода служит интеграл
где P, Q, R — непрерывные функции, определенные в точках двусторонней поверхности S.
Отметим, что если S — замкнутая поверхность, то поверхностный интеграл по внешней стороне ее обозначается 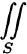
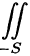
Из определения поверхностного интеграла II рода вытекают следующие его свойства:
- Поверхностный интеграл II рода изменяет знак при перемене стороны поверхности.
- Постоянный множитель можно выносить за знак поверхностного интеграла.
- Поверхностный интеграл от суммы функций равен сумме соответствующих интегралов от слагаемых.
- Поверхностный интеграл II рода по всей поверхности
равен сумме интегралов по ее частям
(аддитивное свойство), если
пересекаются лишь по границе, их разделяющей.
- Если
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
Вычисление поверхностного интеграла II рода
Вычисление поверхностного интеграла II рода сводится к вычислению двойного интеграла.
Пусть функция R(x; у, z) непрерывна во всех точках поверхности S, заданной уравнением z = z(x; y), где z(x; у) — непрерывная функция в замкнутой области D (или 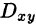
Выберем ту сторону поверхности S, где нормаль к ней образует с осью Oz острый угол. Тогда
Так как 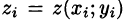
Правая часть этого равенства есть интегральная сумма для функции R(x;y;z(x;y)), непрерывной в области D. Переходя к пределу в равенстве (58.2) при 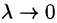
выражающую поверхностный интеграл II рода по переменным х и у через двойной интеграл. Если выбрать вторую сторону, т. е. нижнюю, поверхности S, то полученный двойной интеграл берут со знаком «минус». Поэтому
где 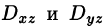
В формуле (58.5) поверхность S задана уравнением у = y(x;z), а в формуле (58.6) — уравнением х = x(y;z). Знаки перед интегралами выбираются в зависимости от ориентации поверхности S (так, в формуле (58.5) берем знак «плюс», если нормаль к поверхности образует с осью Оу острый угол, а знак «минус» — если тупой угол).
Для вычисления общего поверхностного интеграла II рода используют формулы (58.4)-(58.6), проектируя поверхность S на все три координатные плоскости:
Замечание:
Можно показать справедливость равенств
— элемент площади поверхности 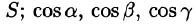
Поверхностные интегралы I и II рода связаны соотношением
Пример:
по верхней стороне части плоскости 2х — Зу + z = 6, лежащей в IV октанте.
Решение:
На рисунке 253 изображена заданная часть плоскости. Нормаль п, соответствующая указанной стороне поверхности, образует с осью Оу тупой угол, а с осями Ох и Oz — острые. В этом можно убедиться, найдя направляющие косинусы нормального вектора 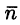
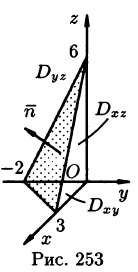
Поэтому перед двойными интегралами в формулах (58.4) и (58.6) следует брать знак «плюс», а в формуле (58.5) — знак «минус». Следовательно,
Формула Остроградского-Гаусса
Связь между поверхностным интегралом II рода по замкнутой поверхности и тройным интегралом по объему, ограниченному этой поверхностью устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y,z), R(x;y;z) непрерывны вместе со своими частными производными первого порядка в пространственной области V, то имеет место формула
где S — граница области V и интегрирование по S производится по ее внешней стороне.
Формула (58.9) называется формулой Остроградского-Гаусса (является аналогом формулы Остроградского-Грина (см. п. 56.3).
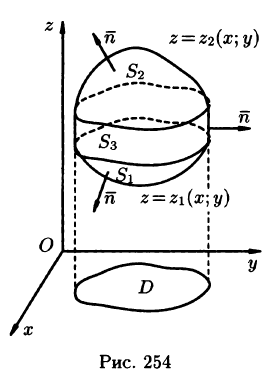
Пусть область V ограничена снизу поверхностью 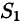
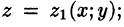
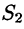
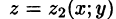
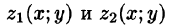
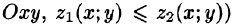
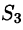
Рассмотрим тройной интеграл
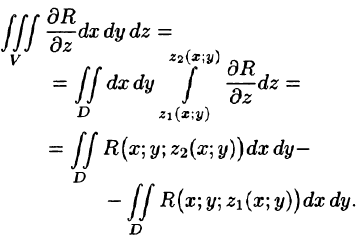
Двойные интегралы в правой части равенства заменим поверхностными интегралами II рода по внешней стороне поверхностей 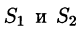
Добавляя равный нулю интеграл 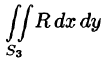
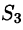
где S — поверхность, ограничивающая область V. Аналогично доказываются формулы
Складывая почленно равенства (58.10), (58.11) и (58.12), получаем формулу (58.9) Остроградского-Гаусса.
Замечания:
- Формула (58.9) остается справедливой для любой области V, которую можно разбить на конечное число областей рассмотренного вида.
- Формулу Остроградского-Гаусса можно использовать для вычисления поверхностных интегралов II рода по замкнутым поверхностям.
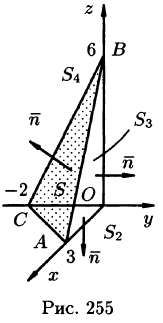
Пример:
где S — внешняя сторона пирамиды, ограниченной плоскостями 2х — Зу + z = 6, х = 0, у = 0, z = 0.
Решение:
По формуле (58.9) находим:
Заметим, что интеграл 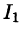
где поверхности 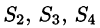
Формула Стокса
Связь между поверхностными и криволинейными интегралами II рода устанавливает следующая теорема.
Теорема:
Если функции P(x;y;z), Q(x;y;z) и R(x;y;z) непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности S, то имеет место формула
где L — граница поверхности S и интегрирование вдоль кривой L производится в положительном направлении (т. е. при обходе границы L поверхность S должна оставаться все время слева).
Формула (58.13) называется формулой Стокса (Д. Г. Стоке — английский математик, физик).
Пусть z = f(x;y) — уравнение поверхности S, функции 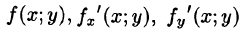
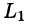
Будем считать, что поверхность S пересекается с любой прямой, параллельной оси Oz, не более чем в одной точке. Выберем верхнюю сторону поверхности S. Рассмотрим сначала интеграл вида
Значения функции Р(х; у; z) на L равны значениям функции P(x; y;z(x;y)) на 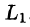
Применим к этому интегралу формулу Остроградского-Грина (см. п. 56.3). Тогда получим:
Преобразуем полученный двойной интеграл в равный ему поверхностный интеграл II рода (см. п. 58.2). Для этого последнее равенство перепишем в виде
(см. 58.7) и используем уравнение нормали к поверхности S (см. (45.3)). Так как выбрана верхняя сторона поверхности S, т. е. 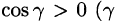
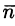
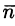
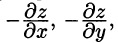
Отсюда 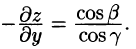
Аналогично получаются при соответствующих условиях еще два равенства:
Складывая почленно три последних равенства, получаем формулу Стокса (58.13).
Отметим, что формулу Стокса (58.13) можно применить и для поверхностей более сложного вида (разбив ее на части рассмотренного выше типа).
Формулу Стокса можно применять для вычисления криволинейного интеграла по замкнутому контуру с помощью поверхностного интеграла.
Из формулы Стокса вытекает, что если выполняются условия
то криволинейный интеграл по произвольному пространственному замкнутому контуру L равен нулю:
Следовательно, в данном случае криволинейный интеграл не зависит от вида пути интегрирования.
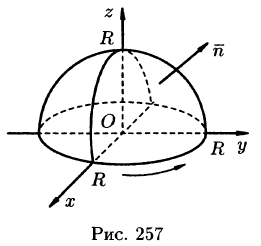
Пример:
Вычислить 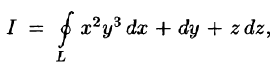
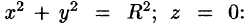
б) используя формулу Стокса, взяв в качестве поверхности полусферу
Решение: Поверхность интегрирования изображена на рисунке 257.
а) Запишем уравнение окружности в параметрической форме:
По формуле (56.7) имеем:
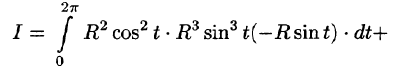
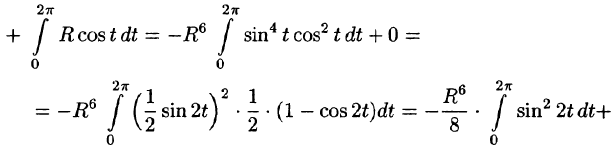
б) По формуле Стокса (58.13) находим:
Переходя к полярным координатам, получаем:
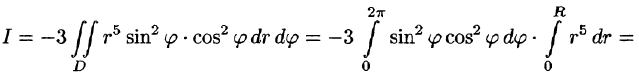
Некоторые приложения поверхностного интеграла II рода
С помощью поверхностного интеграла 11 рода можно найти объем тела, ограниченного сверху поверхностью 
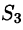
где
Действительно, положив в формуле Остроградского-Гаусса (58.9) 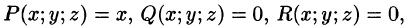
Аналогично, полагая P = 0, Q = у, R = 0, находим еще одну формулу для нахождения объема тела с помощью поверхностного интеграла II рода:
Наконец, положив Р = 0, Q = 0, R = z, по формуле (58.9) находим третью формулу
выражающую объем тела через поверхностный интеграл II рода.
Сложив почленно равенства (58.15)-(58.17) и разделив на три, получим формулу (58.14).
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:





















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Источник


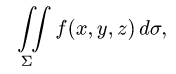
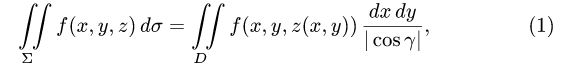
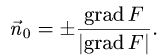
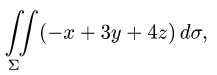
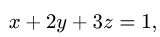
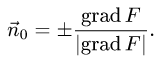
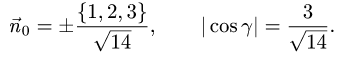
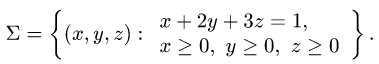
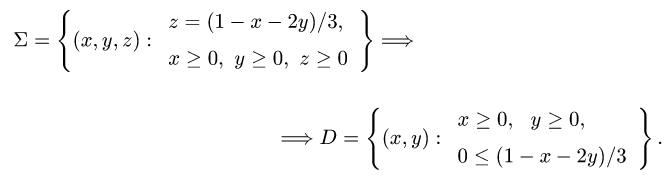
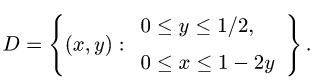
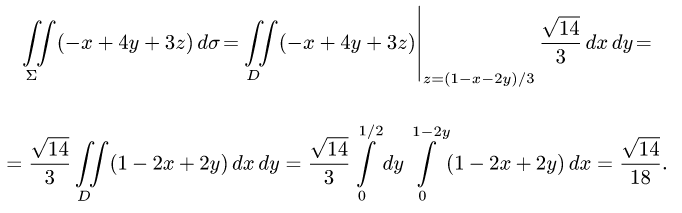
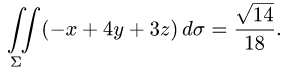
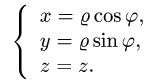
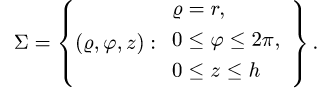
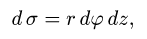
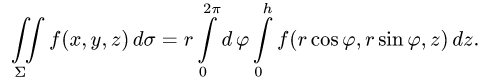
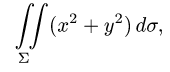
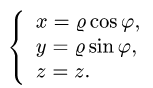
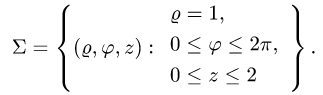
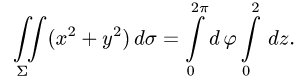
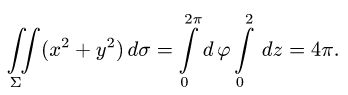
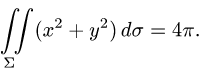
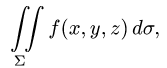
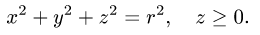
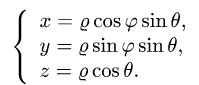
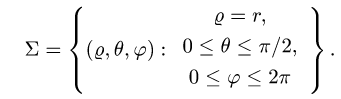
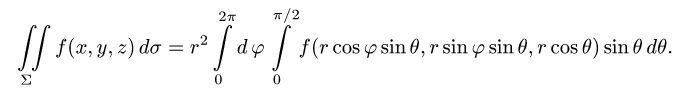
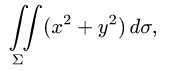
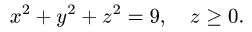
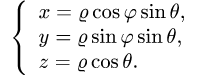
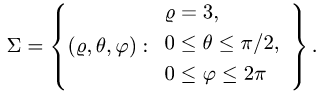
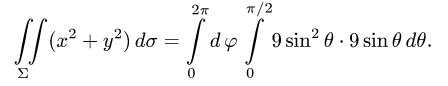
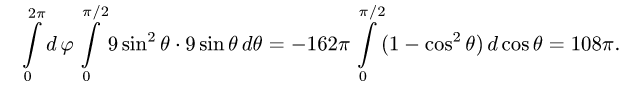
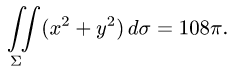


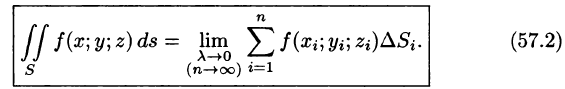
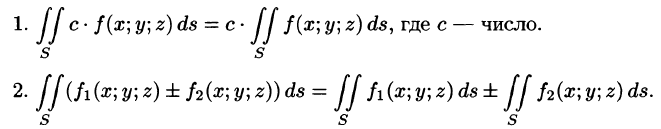
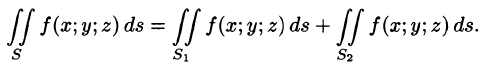
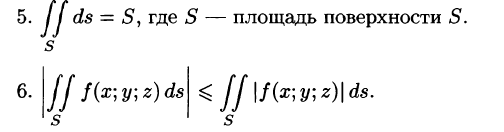
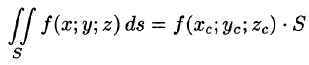
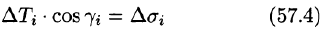
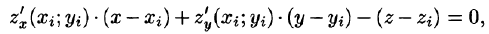
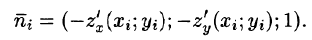
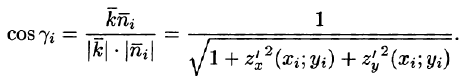
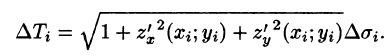
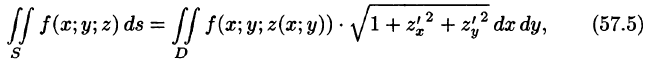
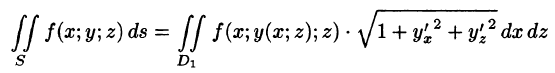
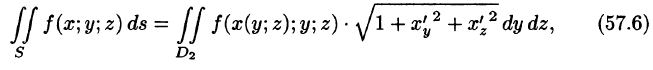
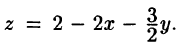
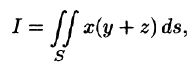
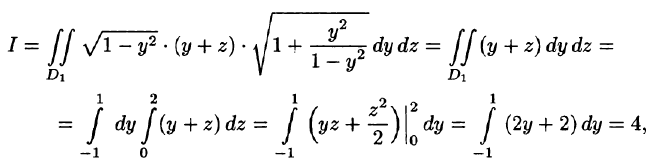
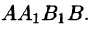
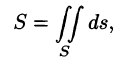
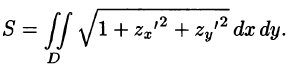
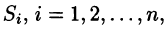 площадь которой обозначим
площадь которой обозначим 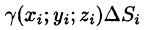 фиктивной однородной области с постоянной плотностью
фиктивной однородной области с постоянной плотностью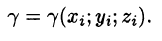
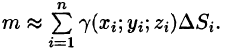
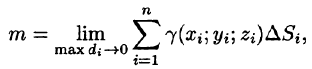
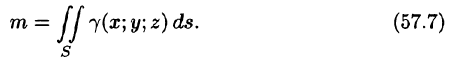
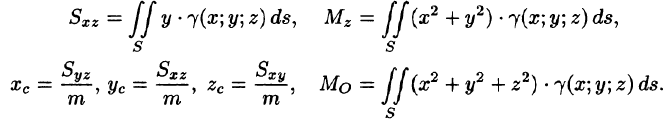
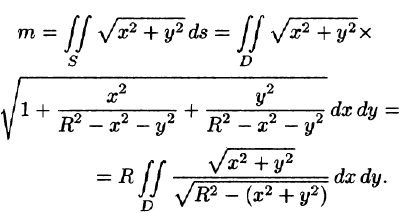
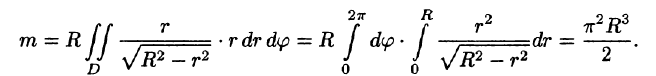
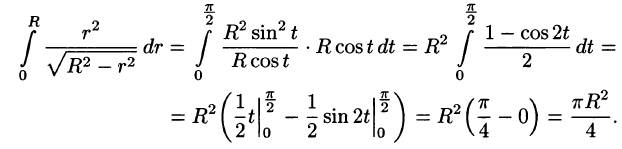

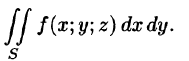
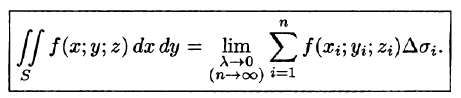
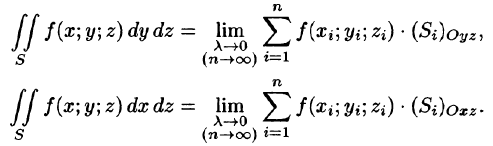
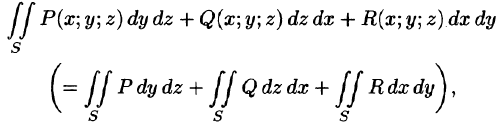
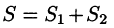 равен сумме интегралов по ее частям
равен сумме интегралов по ее частям 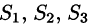 — цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то
— цилиндрические поверхности с образующими, параллельными соответственно осям Oz, Ох, Оу, то