Постройте отрицание высказывания с квантором двумя способами

Построение отрицаний высказываний, содержащих кванторы

Отрицание высказывания с квантором можно построить двумя способами:

1. Поставить перед высказыванием слова “неверно, что”;

2. Для того, чтобы построить отрицание высказывания с квантором общности (существования), достаточно заменить его квантором существования (общности) и построить отрицание предложения, стоящего после квантора, т.е.

= $(х) ;

= «(х) .

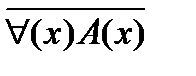
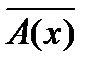
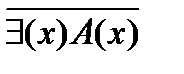
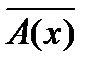
Пример 1: Построим отрицание высказывания “ некоторые однозначные числа делятся на 10”.

— “Неверно, что некоторые однозначные числа делятся на 10”.

-“Все однозначные числа не делятся на 10.”

Пример 2: Построим отрицание высказывания “ каждый четырехугольник является прямоугольником”.

-“Неверно, что каждый четырехугольник является прямоугольником”.

— Некоторые четырехугольники не является прямоугольниками”.

Источник

Высказывательная форма. Высказывания с кванторами. Правила построения отрицаний высказываний с кванторами

Высказывательной формой (или предикатом) называется предложение, содержащее одну или несколько переменных, при подстановке конкретных значений этих переменных образующиеся в высказывания.

Пример. P (x) x+3>5 Q (x;y) x + y = 4 B (x;y;z) x + 2y – 3z > 1

F(x) – кошка серая. В зависимости от количественных переменных говорят об одноместной высказывательной формы (когда 1 переменная) двухместной и трехместной.

С каждой высказывательной формой связано 2 множества:

1. Область определения ( х ) – это множество тех значений переменных, которые обращают высказывательную форму в высказывания.

Х – множество кошек

2. Множество истинности ( Т ) высказывательной формы – это множество тех значений переменных, которые обращают высказывательную форму в истинное высказывание.

Множество – область определения

Переменное множество истинности

F ( x ; y ) x – y = 2

X

Высказывательную форму (одноместную) превратить в высказывание можно представить вместо переменной какое-либо ее значение из области определения, но можно также получить высказывание, если перед высказывательной формой поставить слова: все,любой, каждый, хотя бы один, найдется, существует и так далее. Эти слова называются кванторалии, от латинского слова «квантор» которое обозначает сколько все или не все.

Кванторы делять на две группы:

1. Кванторы общности Ɏ: все, любой, всякий, каждый.

2. Кванторы существования ᴲ: существует, найдется, хотя бы один и т.п.

Структура высказывания квантора.

Все кошки серые

Х – множество кошек

Р(х) : х – серого цвета.

Как устанавливается значение истинности высказывания с кванторами.

1. Истинность высказывания квантора общности устанавливается путем доказательства. Чтобы убедится в ложности высказывания достаточно привести контр-пример.

1. Сумма любых трех последовательных N чисел делится на 3.

n – произвольное N число

2. Все простые числа – нечетные. Высказывание ложное, так как 2 – простое и четное.

1) Для того чтобы установить истинность высказывания квантора существования, достаточно привести 1 пример.

Пример. Существуют некоторые кошки. Чтобы убедится в ложности такого высказывания, нужно привести доказательство.

Пример. а) Существуют N числа кратные 3

ᴲхєN, х:3 Это высказывание истинно, так как х=6.

б) Среди чисел 4,6,8 найдется простое число

Рх; х — простое число

4 – не простое число, т.к. 4 :2

6 – не простое число, т.к. 6:2, 6:3

8 – не простое число, т.к. 8:2, 8:4

Наше высказывание ложно.

Правила построение отрицания высказывания, содержащего кванторы.

I Перед васказыванием поставить слова неверно, что.

Пример. Все кошки серые.

Существуют N числа, кратные 3.

Неверно, что существуют N числа, кратные 3.

II Для того, чтобы построить отрицание высказывания с высказыванием, надо квантор заменить на противоположный и высказывательную форму на ее отрицание.

Ɏ x є X P(x) = ᴲ x є X P (x)

ᴲ x є X P(x) = Ɏ x є X P (x)

Примет. Все ели зеленые.

Найдутся не зеленые ели.

Некоторые попугаи желтые.

Все попугаи не желтые.

Выявить логическую структуру личности, построить отрицание, определить значение истинности.

Ель — лиственное или хвойное дерево.

А : ель – лиственное дерево. Л

В : ель – хвойное дерево. И

А v В = и A v B = A v B : ель не хвойное и не лиственное дерево.

Все треугольники являются равнобедренными. (л)

0 0 – и В : 3 > 6 — л А ^ B – л

А ^ B = А v B : 6 не больше 0 или не меньше 3.

Некоторые слова не могут быть разделены на слоги.

х – множество слов.

Р(х); х – могут быть разделены на слоги.

-умножение и деление в пределах 1000. этап закрепления.

-найти истинность высказывания

2. Обучающимся начальных классов предложено решить задание:

“Вставь нужные числа в “окошки”, чтобы получились верные равенства:

(7+2)+ =7+( + 8); (3 + ) + 7 = ( + 7)+1;

(6 + ) + 4 = ( + 4) + 5; (4+2)+ =5+( +8).”

• При изучении какой темы начального курса математики, возможно, предложить такое задание?

• Приведите рассуждения ученика при выполнении этого задания.

• Сформулируйте в общем виде свойство (правило), о котором идет речь в данном задании.

• Раскройте методику ознакомления детей с этим правилом.

• Приведите примеры использования устных вычислительных приемов, основанных на этом правиле.

Источник

Кванторы

Кроме известных нам логических операций для предикатов вводятся две новые: операция навешивания кванторов существования и общности.

Высказывания «для всех х» (для любого х, для каждого х) называется квантором общности и обозначается х.

Высказывание «существует х» (для некоторых х, хотя бы для одного х, найдется такое х) называется квантором существования и обозначается х.

Высказывание «существует одно и только одно х» (для единственного значения х) называется квантором единственности : ! х.

Например: «Все кустарники являются растениями». Это высказывание содержит квантор общности («все»). Высказывание «существуют числа, кратные 5» содержит квантор существования («существуют»).

Для того чтобы получить высказывание из многоместного предиката, надо связать кванторами каждую переменную. Например, если Р(х; у) – двухместный предикат, то (хХ) (уY) Р(х; у) – высказывание.

Если не каждая переменная связывается квантором, то получается не высказывание, а предикат, зависящий от той переменой, которая не связана квантором. Так, если перед предикатом Р(х; у) поставить квантор у, то получим предикат (уY) Р(х; у), зависящий от переменной х.

Выясним, какие из следующих предложений являются высказываниями, а какие предикатами: а) найдется такое х, что х+ у = 2;

b) для любых х и у имеет место равенство х + у = у + х.

Решение: Выявим логическую структуру данных предложений.

а) Предложение «Найдется такое х, что х + у = 2» можно записать в виде (хR) х + у = 2. Так как квантором связана только переменная х, то рассматриваемое предложение с двумя переменными является предикатом.

b) Предложение «для любых х и у имеет место х + у = у + х» можно записать в виде: (хR) (уR) х + у = у + х, где обе переменные являются связанными. Следовательно, данное предложение является высказыванием.

Если какое-либо предметное переменное в формуле не связано квантором, то его называют свободным переменным.

Например: (х) ху=ух. Здесь переменное у не связано каким-либо квантором, поэтому оно свободно. От него не зависит истинность данного высказывания.

Кванторы (х) (х) называются двойственными друг другу.

Одноименные кванторы можно менять местами, что не влияет на истинность высказывания.

Например: (у) (х) х + у = 5. Это утверждение имеет тот же смысл, что и (х) (у) х + у = 5.

Для разноименных кванторов изменение порядка может привести к изменению истинности высказывания.

Например: (х) (у) х Просмотров 40 454 Комментариев 0

Источник

Построение отрицаний высказываний, содержащих кванторы

Отрицание высказывания с квантором можно построить двумя способами:

1. Поставить перед высказыванием слова “неверно, что”;

2. Для того, чтобы построить отрицание высказывания с квантором общности (существования), достаточно заменить его квантором существования (общности) и построить отрицание предложения, стоящего после квантора, т.е.

= $(х) ;

= «(х) .

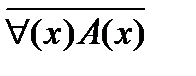
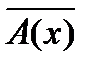
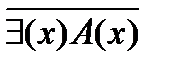
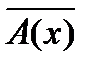
Пример 1: Построим отрицание высказывания “ некоторые однозначные числа делятся на 10”.

— “Неверно, что некоторые однозначные числа делятся на 10”.

-“Все однозначные числа не делятся на 10.”

Пример 2: Построим отрицание высказывания “ каждый четырехугольник является прямоугольником”.

-“Неверно, что каждый четырехугольник является прямоугольником”.

— Некоторые четырехугольники не является прямоугольниками”.

Источник