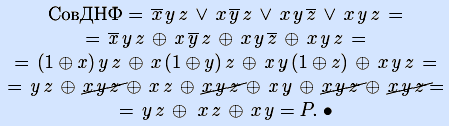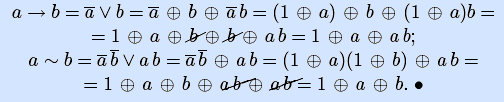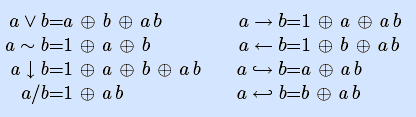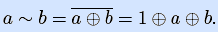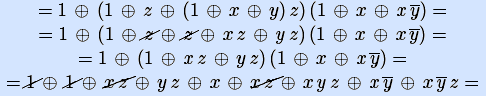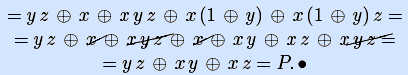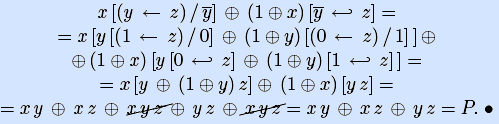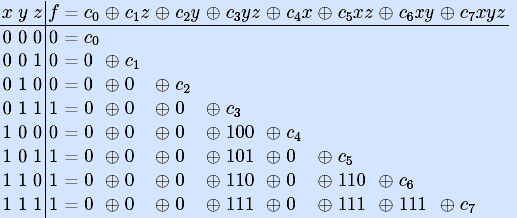Постройте многочлен жегалкина двумя способами

Полином Жегалкина. Методы построения.

Полином (многочлен) Жегалкина представляет собой полином, коэффициентами которого являются числа $0$ или $1$, причем в качестве операций умножения и сложения выступают соответственно конъюнкция и сумма по модулю $2$. Например, для булевой функции $f\left(x_1,\ x_2,\ x_3\right)$ от трех переменных $x_1,\ x_2,\ x_3$ полином Жегалкина будет иметь следующий вид:

$$f\left(x_1,\ x_2,\ x_3\right)=a_0\bigoplus a_1x_1\bigoplus a_2x_2\bigoplus a_3x_3\bigoplus a_<12>x_1x_2\bigoplus a_<13>x_1x_3\bigoplus a_<23>x_2x_3\bigoplus a_<123>x_1x_2x_3.$$

Коэффициенты $a_0,\ a_1,\ \dots ,\ a_<123>\in \left\<0,\ 1\right\>$, то есть могут принимать значения либо $0$, либо $1$ в зависимости от того, какое значение принимает булева функция $f\left(x_1,\ x_2,\ x_3\right)$ на том или ином наборе значений переменных.

С помощью полинома Жегалкина можно представить любую булеву функцию, причем единственных образом. Поэтому можно сказать, что полином Жегалкина является еще одним способом представления булевых функций в алгебре операций $\bigoplus $ — суммы по модулю $2$, $\cdot $ — конъюнкции и константы $1$.

Операция $\bigoplus $ имеет и другие названия: сумма Жегалкина, неравнозначность, исключающее ИЛИ-НЕ. Иногда, для удобства ее обозначения используют привычную запись сложения $+$, но не стоит путать с дизъюнкцией и, тем более, с обычной арифметической операцией сложения. Таблица истинности данной операции имеет вид:

$$\begin<|c|c|>
\hline
x & y & x\bigoplus y \\
\hline
0 & 0 & 0 \\
\hline
0 & 1 & 1 \\
\hline
1 & 0 & 1 \\
\hline
1 & 1 & 0 \\
\hline
\end$$

Сумма $x\bigoplus y$ принимает истинное значение тогда и только тогда, когда истинно одно и только одно составляющее высказывание. Если сравнить таблицы истинности основных логических операций, то можно заметить, что $x\bigoplus y=\overline$. То есть операция сумма Жегалкина $\bigoplus $ есть отрицание эквиваленции.

Для двух введенных операций $\bigoplus ,\ \cdot $ (суммы по модулю 2 и конъюнкции) выполняются все логические законы:

1. Коммутативность: $x\bigoplus y=y\bigoplus x$;
2. Ассоциативность: $\left(x\bigoplus y\right)\bigoplus z=x\bigoplus \left(y\bigoplus z\right)$, то есть результат $x\bigoplus y\bigoplus z$ не зависит от расстановки скобок;
3. Дистрибутивность: $x\left(y\bigoplus z\right)=xy\bigoplus xz$;
4. $x\bigoplus x=0$;
5. $0\bigoplus x=x$;
6. $\overline=x\bigoplus 1$.

Для построения полинома Жегалкина можно использовать различные методы:

• Метод неопределенных коэффициентов;
• Метод треугольника Паскаля;
• Преобразование ДНФ;
• Преобразование СДНФ.

Метод неопределенных коэффициентов

Найдем полином Жегалкина для функции $f\left(x_1,\ x_2,\ x_3\right)=\left(x_1x_2\vee x_3\right)\to <\overline>_2$, используя метод неопределенных коэффициентов. Для этого сначала необходимо построить таблицу истинности данной булевой функции $f\left(x_1,\ x_2,\ x_3\right)$.

$\begin<|c|c|>
\hline
x_1 & x_2 & x_3 & x_1x_2 & x_1x_2\vee x_3 & f\left(x_1,\ x_2,\ x_3\right)=\left(x_1x_2\vee x_3\right)\to <\overline>_2 \\
0 & 0 & 0 & 0 & 0 & 1 \\
\hline
0 & 0 & 1 & 0 & 1 & 1 \\
\hline
0 & 1 & 0 & 0 & 0 & 1 \\
\hline
0 & 1 & 1 & 0 & 1 & 0 \\
\hline
1 & 0 & 0 & 0 & 0 & 1 \\
\hline
1 & 0 & 1 & 0 & 1 & 1 \\
\hline
1 & 1 & 0 & 1 & 1 & 0 \\
\hline
1 & 1 & 1 & 1 & 1 & 0 \\
\hline
\end$

Общий вид полинома Жегалкина для функции $f\left(x_1,\ x_2,\ x_3\right)$ трех переменных $x_1,\ x_2,\ x_3$:

$$f\left(x_1,\ x_2,\ x_3\right)=a_0\bigoplus a_1x_1\bigoplus a_2x_2\bigoplus a_3x_3\bigoplus a_<12>x_1x_2\bigoplus a_<13>x_1x_3\bigoplus a_<23>x_2x_3\bigoplus a_<123>x_1x_2x_3.$$

Последовательно подставляем наборы значений переменных и находим коэффициенты $a_0,\ a_1,\ \dots ,\ a_<123>$.

$f\left(0,\ 0,\ 0\right)=a_0=1;$

$f\left(0,\ 0,\ 1\right)=a_0\bigoplus a_3=1\Rightarrow 1\bigoplus a_3=1\Rightarrow a_3=0;$

$f\left(0,\ 1,\ 0\right)=a_0\bigoplus a_2=1\Rightarrow 1\bigoplus a_2=1\Rightarrow a_2=0;$

$f\left(0,\ 1,\ 1\right)=a_0\bigoplus a_2\bigoplus a_3\bigoplus a_<23>=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus a_<23>=0\Rightarrow 1\bigoplus a_<23>=0\Rightarrow a_<23>=1;$

$f\left(1,\ 0,\ 0\right)=a_0\bigoplus a_1=1\Rightarrow 1\bigoplus a_1=1\Rightarrow a_1=0.$

$f\left(1,\ 0,\ 1\right)=a_0\bigoplus a_1\bigoplus a_3\bigoplus a_<13>=1\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus a_<13>=1\Rightarrow 1\bigoplus a_<13>=1\Rightarrow a_<13>=0;$

$f\left(1,\ 1,\ 0\right)=a_0\bigoplus a_1\bigoplus a_2\bigoplus a_<12>=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus a_<12>=0\Rightarrow 1\bigoplus a_<12>=0\Rightarrow a_<12>=1;$

$f\left(1,\ 1,\ 1\right)=a_0\bigoplus a_1\bigoplus a_2\bigoplus a_3\bigoplus a_<12>\bigoplus a_<13>\bigoplus a_<23>\bigoplus a_<123>=0\Rightarrow 1\bigoplus 0\bigoplus 0\bigoplus 0\bigoplus 1\bigoplus 0\bigoplus 1\bigoplus a_<123>=0\Rightarrow 1\bigoplus a_<123>=0\Rightarrow a_<123>=1;$

Подставляя найденные коэффициенты, получаем полином Жегалкина:

$$f\left(x_1,\ x_2,\ x_3\right)=1\bigoplus x_1x_2\bigoplus x_2x_3\bigoplus x_1x_2x_3.$$

Метод треугольника Паскаля

Построим полином Жегалкина для функции из предыдущего метода, используя треугольник Паскаля.

Поясним, как заполняется треугольник Паскаля. Верхняя строка треугольника задает вектор значений булевой функции $f=\left(11101100\right)$. В каждой строке, начиная со второй, любой элемент такого треугольника вычисляется как сумма по модулю $2$ двух соседних элементов предыдущей строки. Так, элементы второй строки: $1\bigoplus 1=0,\ 1\bigoplus 1=0,\ 1\bigoplus 0=1,\ 0\bigoplus 1=1,\ 1\bigoplus 1=0,\ 1\bigoplus 0=1,\ 0\bigoplus 0=0$. Аналогично вычисляются элементы других строк.

Левой стороне треугольника Паскаля соответствуют наборы значений переменных исходной функции $f\left(x_1,\ x_2,\ x_3\right)$. Соединяя знаком конъюнкции переменные, значения которых в наборе равны $1$, мы получим слагаемое в полиноме Жегалкина. Набору $\left(000\right)$ соответствует $1$, набору $\left(001\right)$ соответствует $x_3$, и т.д.

Поскольку единицам левой стороны треугольника соответствуют слагаемые $1,\ x_2x_3,\ x_1x_2,\ x_1x_2x_3$, то полином Жегалкина:

$$f\left(x_1,\ x_2,\ x_3\right)=1\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3.$$

Преобразование ДНФ

Используя основные законы алгебры логики, приведем сначала данную функцию к ДНФ.

Далее в полученной ДНФ необходимо «избавиться» от дизъюнкции, используя законы де Моргана:

Заменяем каждое отрицание $\overline=1\bigoplus x$ и применяем написанные выше логические законы, получаем:

$\overline<<\overline<<\overline>_1<\overline>_3>x>_2>=1\bigoplus <\overline<<\overline>_1<\overline>_3>x>_2=1\bigoplus \left(1\bigoplus \left(1\bigoplus x_1\right)\left(1\bigoplus x_3\right)\right)x_2=1\bigoplus \left(1\bigoplus 1\bigoplus x_3\bigoplus x_1\bigoplus x_1x_3\right)x_2=1\bigoplus \left(x_3\bigoplus x_1\bigoplus x_1x_3\right)x_2=1\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3$ — полином Жегалкина.

Преобразование СДНФ

$\begin<|c|c|>
\hline
x_1 & x_2 & x_3 & f\left(x_1,\ x_2,\ x_3\right) \\
\hline
0 & 0 & 0 & 1 \\
\hline
0 & 0 & 1 & 1 \\
\hline
0 & 1 & 0 & 1 \\
\hline
0 & 1 & 1 & 0 \\
\hline
1 & 0 & 0 & 1 \\
\hline
1 & 0 & 1 & 1 \\
\hline
1 & 1 & 0 & 0 \\
\hline
1 & 1 & 1 & 0 \\
\hline
\end$

Для построения СДНФ по таблице истинности выбираем наборы, на которых функция $f$ принимает значение, равное 1. Если значение переменной в этом наборе равно 0, то она берется с отрицанием, если значение переменной равно 1, то переменная берется без отрицание. Соединив знаком конъюнкции переменные соответствующего набора, получим элементарную конъюнкцию. Тогда дизъюнкция всех таких элементарных конъюнкций есть СДНФ.

Чтобы построить полином Жегалкина через СДНФ, необходимо исключить операции дизъюнкции и отрицания, затем раскрыть скобки.

$f\left(x_1,\ x_2,\ x_3\right)=<\overline>_1<\overline>_2<\overline>_3\bigoplus <\overline>_1<\overline>_2x_3\bigoplus <\overline>_1x_2<\overline>_3\bigoplus x_1<\overline>_2<\overline>_3\bigoplus x_1<\overline>_2x_3=\left(1\bigoplus x_1\right)\left(1\bigoplus x_2\right)\left(1\bigoplus x_3\right)\bigoplus \left(1\bigoplus x_1\right)\left(1\bigoplus x_2\right)x_3\bigoplus \left(1\bigoplus x_1\right)x_2\left(1\bigoplus x_3\right)\bigoplus x_1\left(1\bigoplus x_2\right)\left(1\bigoplus x_3\right)\bigoplus x_1\left(1\bigoplus x_2\right)x_3=1\bigoplus x_3\bigoplus x_2\bigoplus x_2x_3\bigoplus x_1\bigoplus x_1x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3\bigoplus x_3\bigoplus x_2x_3\bigoplus x_1x_3\bigoplus x_1x_2x_3\bigoplus x_2\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3\bigoplus x_1\bigoplus x_1x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3\bigoplus x_1x_3\bigoplus x_1x_2x_3=1\bigoplus x_2x_3\bigoplus x_1x_2\bigoplus x_1x_2x_3$ — полином Жегалкина.

Источник

Постройте многочлен жегалкина двумя способами

Рассмотрим алгоритмы построения полинома Жегалкина булевой функции, заданной различными способами, а именно: совершенной ДНФ, произвольной ДНФ, формулой и таблицей истинности.

Алгоритм построения полинома Жегалкина по СовДНФ (основан на доказательстве теоремы о существовании полинома Жегалкина).

Начало. Задана совершенная ДНФ функции f(x₁, …, x_n).

Шаг 1. Заменяем каждый символ дизъюнкции на символ дизюнкции с исключением.

Шаг 2. Заменяем каждую переменную с инверсией x равносильной формулой x 1.

Шаг 3. Раскрываем скобки.

Шаг 4. Вычеркиваем из формулы пары одинаковых слагаемых.

Конец. Получен полином Жегалкина функции f(x₁, …, x_n).

Пример. Найдем полином Жегалкина мажоритарной булевой функции по ее совершенной ДНФ.

Алгоритм построения полинома Жегалкина по ДНФ (основан на равносильности K₁ K₂= K₁ K₂ K₁K₂).

Начало. Задана произвольная ДНФ функции f(x₁, …, x_n).

Шаг 1. Разбиваем ДНФ на пары конъюнкций, предпочтительно ортогональных (если число конъюнкций нечетно, одна из них остается без пары).

Шаг 2. Заменяем дизъюнкцию каждой пары конъюнкций K₁ K₂ формулой K₁ K₂ K₁K₂ или формулой K₁ K₂, если K₁ и K₂ ортогональны.

Шаг 3. В полученной формуле находим очередную дизъюнкцию A₁ A₂и заменяем ее формулой A₁ A₂ A₁A₂. Повторяем шаг 3 до тех пор, пока это возможно.

Шаг 4. Заменяем каждую переменную с инверсией x равносильной формулой x 1.

Шаг 5. Раскрываем скобки.

Шаг 6. Вычеркиваем из формулы пары одинаковых слагаемых.

Конец. Получен полином Жегалкина функции f(x₁, …, x_n).

Пример. Найдем полином Жегалкина мажоритарной функции по ДНФ.

Отметим, что полиномы мажоритарной функции, полученные в двух последних примерах, совпадают с точностью до порядка конъюнкций, и это естественно (по теореме о единственности полинома Жегалкина).

Способ 1 основан на предварительном преобразовании формулы в ДНФ (любым известным нам способом). Затем ДНФ преобразуется в полином Жегалкина по только что изученному алгоритму.

Примеры. Получим полиномы Жегалкина двух элементарных булевых функций: импликации и эквивалентности, представив их предварительно кратчайшими ДНФ.

Аналогично можно получить полиномы Жегалкина всех элементарных булевых функций (оставим читателю их вывод).

Константы 0 и 1, тождественная функция, а также конъюнкция ab и дизъюнкция с исключением ab уже являются полиномами Жегалкина. Полином Жегалкина инверсии a =1a.

Заметим, что некоторые из приведенных полиномов могут быть получены гораздо проще, в частности,

Способ 2. Если булева функций задана произвольной формулой, то ее полином Жегалкина можно получить подстановкой в формулу вместо элементарных булевых функций их полиномов.

Пример. Найдем полином Жегалкина мажоритарной функции, заданной формулой:

[ подставим в формулу полином Жегалкина штриха Шеффера 1 ab при a=(xy) z, b=x y ]

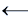
[ подставим полиномы Жегалкина обратной импликации 1 b ab при a=xy, b=z и импликации 1 a ab при a=x, b= y ]

[ подставим полином Жегалкина эквивалентности 1 x y, раскроем скобки, и вычеркнем появившиеся при этом пары одинаковых слагаемых ]

[заменим инверсию ее полиномом Жегалкина, раскроем скобки и вычеркнем пары одинаковых слагаемых ]

Полином, естественно, совпадает с полученными ранее по совершенной и произвольной ДНФ.

Способ 3. Если булева функций задана произвольной формулой, то ее полином Жегалкина можно получить, используя специальное разложение функции.

Определение. Разложением Дэвио называется следующее разложение булевой функции f(x₁, …, x_n по переменной x_i:

Разложение Дэвио непосредственно следует из разложения Шеннона, если учесть, что слагаемые в последнем ортогональны, и что x _i=x_i 1.

Пример. Найдем разложение Дэвио по переменной x мажоритарной булевой функции, заданной формулой.

Для получения полинома Жегалкина необходимо продолжить разложение подформул, не являющихся дизъюнкцией с исключением элементарных конъюнкций, пока не получится формула над <,, – >. Если в такой формуле заменить инверсии x на x 1, раскрыть скобки и вычеркнуть пары одинаковых слагаемых, то получится полином Жегалкина.

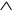
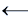
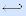
Пример. Продолжив предыдущий пример, получим полином Жегалкина мажоритарной функции. Для этого разложим подформулы (y z) / y и y z по переменной y:

Полином Жегалкина, естественно, совпадает с полученными ранее.

Алгоритм построения полинома Жегалкина по таблице истинности (основан на методе неопределенных коэффициентов).

Продемонстрируем идею метода на примере произвольной булевой функции двух аргументов f(x,y). Представим ее полиномом Жегалкина в форме с коэффициентами

Подставив в данное равенство наборы значений аргументов, получим систему из четырех линейных уравнений с четырьмя неизвестными коэффициентами: c₀, c₁ c₂, c₃.

f(0,0) = c₀ c₁0 c₂0 c₃0 0 = c₀

f(0,1) = c₀ c₁1 c₂0 c₃0 1 = c₀ c₁

f(1,0) = c₀ c₁0 c₂1 c₃1 0 = c₀ c₂

f(1,1) = c₀ c₁1 c₂1 c₃1 1 = c₀ c₁ c₂ c₃

Заметим, что наборы подставлены в равенство в естественном порядке, и система имеет треугольный вид: в первом уравнении обратились в ноль все слагаемые, следующие за c₀, во втором – следующие за c₁ и так далее. Значит, коэффициент c₀ можно получить из первого уравнения и подставить его в остальные. Тогда c₁ можно получить из второго уравнения, и так далее.

В общем случае для функции n аргументов получается система треугольного вида из 2 n линейных уравнений с 2 n неизвестными – коэффициентами полинома Жегалкина.

Пример. Найдем полином Жегалкина мажоритарной булевой функции, заданной таблицей истинности, последовательно вычисляя коэффициенты полинома и подставляя их в остальные уравнения.

Из первого уравнения следует, что c₀=0. Из второго и третьего уравнений следует, что c₁=0 и c₂=0, значит, c₁z и c₂y тождественно равны нулю. Из четвертого уравнения получаем c₃=1, значит, надо вычислять значения конъюнкции c₃yz в остальных уравнениях. Аналогично получаем c₄=0, c₅=1, c₆=1 и c₇=0. Найден вектор коэффициентов полинома Жегалкина мажоритарной функции π=00010110, и сам полином P=yz xz xy, который, естественно, совпадает с полученными ранее. •

Источник