- ДНФ, КНФ, СДНФ, СКНФ, полином Жегалкина
- Задачи и решения о представлении булевых функций
- Нормальные формы (КНФ, СКНФ, ДНФ и СДНФ): примеры решений
- Многочлен Жегалкина: примеры решений
- Решение задач на заказ
- Построить СКНФ двумя способами
- СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице
- СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице
- Пример построения СКНФ для медианы
- Примеры СКНФ для некоторых функций
- Далее:
- Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения
- Что такое СДНФ
- Что такое СКНФ
- Правила построения по таблице истинности
- Дизъюнктивная форма
- Конъюнктивная форма
- Алгоритм приведения к СДНФ и СКНФ
- Доказательство эквивалентности
- Поглощение
- Склеивание
- Обобщенное склеивание
- Расщепление
- Примеры с решением
ДНФ, КНФ, СДНФ, СКНФ, полином Жегалкина
На этой странице вы найдете готовые примеры задач, связанных с упрощением и преобразованием булевых функций к нормальным формам (ДНФ, КНФ), совершенным нормальным формам (СДНФ, СКНФ) и к каноническому многочлену Жегалкина.
Самый простой метод построения совершенной дизъюнктивной и конъюнктивной нормальных форм — с помощью таблиц истинности. Для перехода к ДНФ и КНФ используют методы эквивалентных преобразований, правила де Моргана, свойства поглощения, правило Блейка и т.п.
Полином Жегалкина может быть построен как с помощью последовательных преобразований, так и по таблице истинности (метод неопределенных коэффициентов).
Все эти примеры разобраны ниже. Типовые задачи снабжены подробным решением, формулами, пояснениями. Используйте их, чтобы научиться решать подобные задачи или закажите решение своей работы нам.
Другие примеры решений о булевых функциях:
Задачи и решения о представлении булевых функций
Нормальные формы (КНФ, СКНФ, ДНФ и СДНФ): примеры решений
Задача 1. Привести к КНФ и СКНФ.
$$((((A\to B)\to \bar A) \to \bar B) \to \bar C).$$
Задача 2. С помощью эквивалентных преобразований построить д.н.ф. функции:
$$f(x)=(\overline
Задача 3. Используя СКНФ, найдите наиболее простую формулу алгебры высказываний от четырех переменных, принимающую значение 0 на следующих наборах значений переменных, и только на них:
Задача 4. Привести данные выражения к ДНФ, пользуясь правилами де Моргана. Если возможно, сократить ДНФ, используя свойство поглощения и правило Блейка.
Многочлен Жегалкина: примеры решений
Задача 5. Представив функцию формулой над множеством связок $\<\&, -\>$, преобразовать затем полученную формулу в полином Жегалкина функции $f(x)$ (используя эквивалентности):
$$f(x) = (x_1 \vee x_2) \cdot (x_2 | x_3)$$
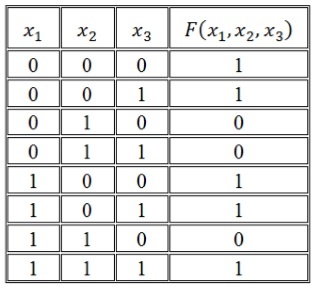
Задача 6. Задана булева функция: $$ f(x_1, x_2, x_3) = \overline
Б) Найти многочлен Жегалкина.
Задача 7. Для заданной логической функции перейти к полиному Жегалкина.
Решение задач на заказ
Выполняем для студентов очников и заочников решение заданий, контрольных и практических работ по любым разделам булевой алгебры, в том числе задачи по построению СДНФ, СКНФ, полинома Жегалкина на заказ. Также оказываем помощь в сдаче тестов. Подробное оформление, таблицы, графики, пояснение, использование специальных программ при необходимости. Стоимость примера от 100 рублей , оформление производится в Word, срок от 2 дней.
Источник
Построить СКНФ двумя способами
(XvZ=>Y)X
1. С помощью элементарных преобразований.
2. С помощью таблицы истинности.
Таблицу составил. Помогите пожалуйста сделать с помощью элементарных преобразований.
Построить СКНФ двумя способами
Для заданной формулы F, представляющей логическую функцию f, построить совершенную конъюнктивную.
Построить СКНФ двумя способами
Для заданной формулы F, представляющей логическую функцию f, построить совершенную дизъюнктивную.
Составить СДНФ и СКНФ (двумя способами)
Всем доброго времени суток. У меня такая проблема: перевелся в другой институт. В связи с переводом.
Записать формулы в СДНФ или СКНФ двумя способами
Здравствуйте друзья! Помогите пожалуйста решить этот пример
СДНФ и СКНФ представить 2 способами
Помогите решить мне никогда с этим не справиться)))) Прикрепила файл с заданием

найти ДНФ, КНФ. СДНФ, СКНФ, найти двумя способами (путем равносильных преобразований и используя.

С помощью равносильных преобразований построить совершенную нормальную форму ф-ции f .
!(x*z)->(x->y)+z*!y ! — это отрицание Не получается построить СКНФ, помогите пожалуйста!
Источник
СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице
СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице
- Услуги проектирования
- Алгебра логики [Г.И. Просветов, Е.А. Фоминых, Ф.Г. Кораблёв]
- СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице
СКНФ. Теорема о представлении в виде СКНФ. Построение СКНФ по таблице
Простой дизъюнкцией < англ. inclusive disjunction >или дизъюнктом < англ. disjunct >называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная встречается не более одного раза.
- полная, если в неё каждая переменная (или её отрицание) входит ровно один раз;
- монотонная, если она не содержит отрицаний переменных.
Конъюнктивная нормальная форма, КНФ < англ. conjunctive normal form, CNF >нормальная форма, в которой булева функция имеет вид конъюнкции нескольких простых дизъюнктов.
Пример КНФ: $f(x,y) = (x \lor y) \land (y \lor \neg < z >)$
Совершенная конъюнктивная нормальная форма, СКНФ < англ. perfect conjunctive normal form, PCNF >— это такая КНФ, которая удовлетворяет условиям:
- в ней нет одинаковых простых дизъюнкций
- каждая простая дизъюнкция полная
Пример СКНФ: $f(x,y,z) = (x \lor \neg < y >\lor z) \land (x\lor y \lor \neg < z >)$
Теорема: Для любой булевой функции $f(\vec < x >)$, не равной тождественной единице, существует СКНФ, ее задающая.
Доказательство: Поскольку инверсия функции $\neg < f >(\vec x)$ равна единице на тех наборах, на которых $f(\vec x)$ равна нулю, то СДНФ для $\neg < f >(\vec x)$ можно записать следующим образом:
$\neg < f >(\vec x) = \bigvee\limits_ < f(x^ < \sigma_ < 1 >> , x^ < \sigma_ < 2 >> , . ,x^ < \sigma_ < n >> ) = 0 > (x_ < 1 >^ < \sigma_ < 1 >> \wedge x_ < 2 >^ < \sigma_ < 2 >> \wedge . \wedge x_ < n >^ < \sigma_ < n >> ) $, где $ \sigma_ < i >$ обозначает наличие или отсутствие отрицание при $ x_ < i >$
Найдём инверсию левой и правой части выражения:
Применяя дважды к полученному в правой части выражению правило де Моргана, получаем: $ f(\vec x) = \bigwedge \limits_ < f(x^ < \sigma_1 >, x^ < \sigma_2 >, \dots ,x^ < \sigma_n >) = 0 > $ $(\neg < x_1^ < \sigma_1 >> \vee \neg < x_2^ < \sigma_2 >> \vee \dots \vee \neg < x_n^ < \sigma_n >> ) $
Последнее выражение и является СКНФ. Так как СКНФ получена из СДНФ, которая может быть построена для любой функции, не равной тождественному нулю, то теорема доказана.
Алгоритм построения СКНФ по таблице истинности
- В таблице истинности отмечаем те наборы переменных, на которых значение функции равно $0$.
- Для каждого отмеченного набора записываем дизъюнкцию всех переменных по следующему правилу: если значение некоторой переменной есть $0$, то в дизъюнкцию включаем саму переменную, иначе ее отрицание.
- Все полученные дизъюнкции связываем операциями конъюнкции.
Пример построения СКНФ для медианы
1). В таблице истинности отмечаем те наборы переменных, на которых значение функции равно $0$.
| x | y | z | $ \langle x,y,z \rangle $ |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2). Для каждого отмеченного набора записываем конъюнкцию всех переменных по следующему правилу : если значение некоторой переменной есть $0$, то в дизъюнкцию включаем саму переменную, иначе ее отрицание.
| x | y | z | $ \langle x,y,z \rangle $ | |
| 0 | 0 | 0 | 0 | $( x \lor y \lor z)$ |
| 0 | 0 | 1 | 0 | $( x \lor y \lor \neg < z >)$ |
| 0 | 1 | 0 | 0 | $(x \lor \neg < y >\lor z)$ |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | $(\neg < x >\lor y \lor z)$ |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 |
3). Все полученные дизъюнкции связываем операциями конъюнкции.
$ \langle x,y,z \rangle = ( x \lor y \lor z) \land (\neg < x >\lor y \lor z) \land (x \lor \neg < y >\lor z) \land ( x \lor y \lor \neg < z >)$
Примеры СКНФ для некоторых функций
Стрелка Пирса: $ x \downarrow y = (\neg < x >\lor < y >) \land ( < x >\lor \neg < y >) \land (\neg < x >\lor \neg < y >) $
Исключающее или: $ x \oplus y \oplus z = (\neg < x >\lor \neg < y >\lor z) \land (\neg < x >\lor y \lor \neg < z >) \land (x \lor \neg < y >\lor \neg < z >) \land (x \lor y \lor z)$
Далее:
Частные случаи векторных полей
Несобственные интегралы по неограниченной области
Специальные векторные поля
Критерий полноты
Свойства потока векторного поля
Вычисление двойного интеграла
Вычисление двойного интеграла. Двукратный интеграл
Равносильные формулы алгебры высказываний
Вычисление площади поверхности
Полином Жегалкина. Пример.
Примеры применения цилиндрических и сферических координат
Класс $T_1$. Теорема о замкнутости класса $T_1$
Класс M. Теорема о замкнутости класса M
Линейный интеграл и циркуляция векторного поля
Огравление $\Rightarrow $
Источник
Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения
Что такое СДНФ
Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.
Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).
СДНФ — совершенная дизъюнктивная нормальная форма формулы. СДНФ — способ написания функции алгебры логики в качестве логического выражения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
СДНФ формулы — это равнозначная ей формула, которая представляет собой дизъюнкцию элементарных конъюнкций, при которых функция достигает показателя «1».
ДНФ выглядит следующим образом:
СДНФ обладает некоторыми определенными свойствами:
- включает различные элементарные конъюнкции;
- все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
- ни в одном логическом слагаемом не содержится переменная и её отрицание.
К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.
При построении таблицы истинности важно помнить, что логические переменные со значением «0» необходимо брать с отрицанием.
Что такое СКНФ
СКНФ — совершенная конъюнктивная нормальная форма. Формулу можно назвать таковой, когда она — конъюнкция неповторяющихся элементарных дизъюнкций.
Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:
- в ней отсутствуют одинаковые элементарные дизъюнкции;
- дизъюнкции не содержат одинаковые переменные;
- все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.
Правила построения по таблице истинности
Дизъюнктивная форма
Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.
Конъюнктивная форма
Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.
Алгоритм приведения к СДНФ и СКНФ
Рассмотрим логическую функцию в виде таблицы истинности.
Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:
- Отметить наборы переменных, значение функции F на которых равно 1.
- Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная. В случае противного результата, в конъюнкцию включается ее отрицание.
- Связать полученные конъюнкции операциями дизъюнкции.
Построим совершенную ДНФ:
И как результат получим следующую СДНФ:
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:
- Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
- Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.
- Связать полученные дизъюнкции операциями конъюнкции.
Построим совершенную КНФ:
И как результат получим следующую СКНФ:
Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.
Доказательство эквивалентности
Эквивалентность — понятие, означающее, что две и более формул представляют одну и ту же функцию. Для обозначения эквивалентности могут использоваться следующие знаки: \( \equiv , = , \Leftrightarrow .\)
Доказать эквивалентность формул можно двумя способами.
- Первый заключается в построении и сравнении таблиц истинности обеих функций. В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
- Второй вариант — метод эквивалентных преобразований. Суть этого метода — построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей.
Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью.
Поглощение
Склеивание
Обобщенное склеивание
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)
\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)
Расщепление
\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)
Примеры с решением
Задача №1
Приведите к СКНФ \(((((A\rightarrow B)\rightarrow\overline A)\rightarrow\overline B)\rightarrow\overline C)\) .
Через применение закона де Моргана и правила \( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:
\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)
\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline<((\overline A\;\vee\;B)>\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)
\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline<(\overline<(\overline A\vee B)>\;\vee\;\overline A\;)>\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)
\(=\;((\overline<(\overline A\;\vee\;B)>\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)
\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)
\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)
Далее приведем выражение к КНФ:
\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)
Далее приведем выражение к СКНФ:
\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)
\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)
Задача №2
Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)
\(f(\widetilde x^3) = (\overline
\(f(\widetilde x^3) = (\overline
\(=(\overline
Источник