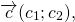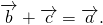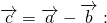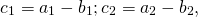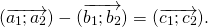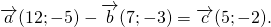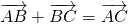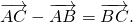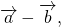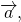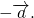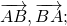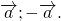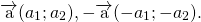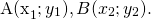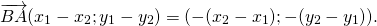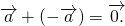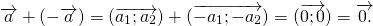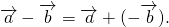Разность векторов
Разность векторов
— это такой вектор
который в сумме с вектором b даёт вектор a:
На основе определения находим координаты вектора
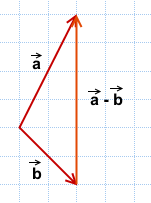
Как построить разность двух векторов?
Из равенства
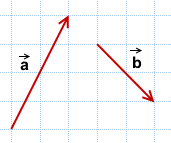
правило построения разности двух векторов
Чтобы построить вектор, равный разности векторов
надо отложить оба вектора от одной точки. Разность векторов — вектор, проведённый от конца вычитаемого b к концу уменьшаемого a.
Противоположные векторы — это противоположно направленные векторы одинаковой длины.
Вектор, противоположный вектору
Примеры противоположных векторов:
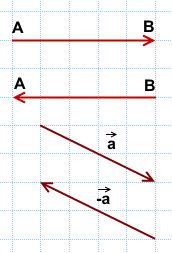
Свойства противоположных векторов:
1) Противоположные векторы имеют противоположные координаты:
Пусть даны точки
2) Сумма противоположных векторов равна нулевому вектору:
2 способ построения разности векторов
Чтобы построить разность векторов
можно к вектору a прибавить вектор, противоположный вектору b:
То есть вычитание векторов заменяем сложением уменьшаемого с вектором, противоположным вычитаемому.
Источник
Вычитание векторов. Как найти разность векторов
Вы будете перенаправлены на Автор24
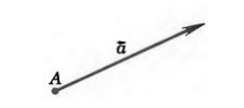
Откладывание вектора от данной точки
Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Введем следующую теорему:
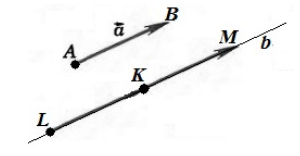
От любой точки $K$ можно отложить вектор $\overrightarrow$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Вычитание векторов. Правило первое
Пусть нам даны векторы $\overrightarrow$ и $\overrightarrow$.
Готовые работы на аналогичную тему
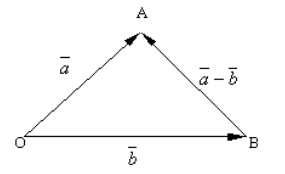
Построение разности двух векторов рассмотрим с помощью задачи.
Решение.
Рисунок 3. Разность двух векторов
По правилу треугольника для построения суммы двух векторов видим, что
Из определения 2, получаем, что
Вычитание векторов. Правило второе
Вспомним следующее необходимое нам понятие.
Вектор $\overrightarrow
Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.
Доказательство.
По определению 2, имеем
Прибавим к обеим частям вектор $\left(-\overrightarrow\right)$, получим
Так как векторы $\overrightarrow$ и $\left(-\overrightarrow\right)$ противоположны, то $\overrightarrow+\left(-\overrightarrow\right)=\overrightarrow<0>$. Имеем
Теорема доказана.
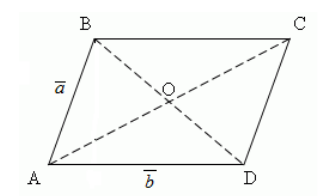
Пример задачи на понятие разности векторов
Рисунок 4. Параллелограмм
Решение.
а) Произведем сложение по правилу треугольника, получим
Из первого правила разности двух векторов, получаем
б) Так как $\overrightarrow
По теореме 2, имеем
Используя правило треугольника, окончательно имеем
Источник
Геометрия, 9 класс, урок: «Вычитание векторов»
ГЕОМЕТРИЯ, 9 КЛАСС, УРОК: «ВЫЧИТАНИЕ ВЕКТОРОВ»
Тема: Вычитание векторов
Знать, какой вектор является разностью двух векторов, теорему о разности векторов.
Уметь строить разность двух векторов двумя способами, применять эти знания при решении задач.
I. Организационный момент: назвать уели урока.
II. Проверка пройденного материала:
1. Как называются векторы, имеющие равные модули и противоположно направленные?
Б) противоположно направленные
2. Тело переместили из точки А в точку В, а потом из точки В в точку С. Какой вектор представляет суммарное перемещение тела?
А) 
Б) 
В) 
3. Закончите предложение:
Суммой двух векторов называется вектор, построенный по правилу. (треугольника)
4. Вставьте пропущенное слово:
Чтобы сложить два неколлинеарных вектора 
и
, нужно отложить от произвольной точки О векторы 
= и 
= и построить. ОАСВ, тогда 
=+
5. Изображенный на рисунке способ построения суммы нескольких векторов называется правилом.
III. Объяснение нового материала:
Вычитание векторов, как и вычитание чисел, — это действие, обратное сложению. Разность двух векторов и называется такой вектор 
, который в сумме с вектором дает вектор . Разность векторов и обозначается так: — . Построить разность векторов и можно следующим образом. Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда вектор 
и будет разностью — , поскольку
=+. Итак, == — = — .
Вычитание векторов можно свести к сложению точно так же, как и в случае чисел а и b:
а — b = а + (- b), где числа b и + (- b) — противоположные.
Итак, нам надо доказать, что результат вычитания вектора из вектора тот же, что и результат сложения векторов а + (- b).
2. Теорема о разности двух векторов.
Теорема (о разности векторов)
Для любых векторов и справедливо равенство — = + (- ).
Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда, согласно определению, разность векторов и есть вектор , т. е. = — = — . По правилу треугольника = 
+ . Кроме того, = — = —. Поэтому — = = + = (-) + =+(-)=+(-). Теорема доказана.
3. Построение разности векторов.
Доказанная теорема подсказывает еще один способ построения разности векторов и .
Отложим от произвольной точки О отложим вектор = , затем от точки А отложим вектор 
= —. Тогда по теореме о разности двух векторов — = + (-), поэтому — = + = . Итак, мы построили разность векторов и .
Выводы по уроку:
1. Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор .
2. Теорема ( о разности двух векторов): Для любых векторов и справедливо равенство:
— = + (-).
IV. Закрепление полученных знаний.
А) Разностью двух векторов и называется такой вектор , построенный по правилу треугольника.
Б) Разностью двух векторов и называется такой вектор , который получается после ряда последовательных сложений
В) Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор
2. Какой вектор, изображенный на рисунке, является разностью векторов и ?
А)
Б)
В)
3. № 000. Дан треугольник АВС. Выразите векторы = и = вектор 
.
а) —
б) —
в) +
4. № 000. Сторона равностороннего треугольника АВС равна а. Модуль ½ — ½ = а
V. Подведение итогов.
VI. Задание на дом: п.82, №№ 000, 756, 767
Источник
